量子领域的机器学习&人工智能(三)(Machine learning & artificial intelligence in the quantum domain)
Machine learning & artificial intelligence in the quantum domain
-
- 摘要( Abstract)
- Ⅵ.机器学习的量子增强( QUANTUM ENHANCEMENTS FOR MACHINE LEARNING)
-
- A. 学习效率的提高:样本复杂性(Learning efficiency improvements: sample complexity)
-
- 1. 量子PAC学习( Quantum PAC learning)
- 2. 从会员查询中学习(Learning from membership queries)
- B.学习能力的提高(Improvements in learning capacity)
-
- 1. 幅度编码的容量(Capacity from amplitude encoding)
- 2. 通过量化的Hopfield网络的能力( Capacity via quantized Hopfield networks)
- C. 运行时间的改进:计算复杂性( Run-time improvements: computational complexity)
-
- 1. 通过模拟退火优化加速(Speed-up via adiabatic optimization)
- 2. 加快电路架构(Speed-ups in circuit architectures)
原文作者:Vedran Dunjko;Hans J. Briegel
翻译者:Wendy
摘要( Abstract)
量子信息技术和只能学习系统都是新型的技术,它们很可能在未来对我们的社会产生变革性的影响。各个基础研究领域–量子信息(QI)与机器学习(ML)和人工智能(AI)–各自都有特定的问题和挑战,迄今为止,这些问题和挑战已被大量独立研究。然而,在最近的工作中,研究人员一直在探索这些领域在多大程度上可以真正相互学习和受益的问题。QML探索了量子计算与机器学习之间的相互作用,研究了如何将一个领域的结果和技术用于解决另一领域的问题。最近,我们见证了两个方面的重大突破。 例如,量子计算在加快机器学习问题的速度中找到了至关重要的应用,这对于“大数据”领域至关重要。相反,机器学习已经渗透到许多尖端技术中,并可能成为先进量子技术的重要工具。 除了数据分析中的量子加速或量子实验中使用的经典机器学习优化之外,理论上还证明了交互式学习任务的量子增强,突出了量子增强的学习代理的潜力。最后,探索将人工智能用于量子实验的设计以及自主进行部分真正研究的工作,报告了他们的首次成功。 除了相互增强的主题(探索ML / AI对量子物理学的作用,反之亦然)之外,研究人员还提出了学习和AI概念的量子概括的基本问题。 这涉及在量子力学充分描述的世界中学习和智力的意义的问题。 在这篇综述中,我们描述了在量子领域研究机器学习和人工智能的广泛研究中的主要思想和最新进展。
Ⅵ.机器学习的量子增强( QUANTUM ENHANCEMENTS FOR MACHINE LEARNING)
量子机器学习最受关注的方面之一是关于 量子效应是否可以帮助我们更有效地解决经典学习任务的问题,理想地反映了量子计算的成功。甚至在Shor和Grover的开创性工作(Shor,1997; Goverr,1996)之前,就已经首次尝试将量子信息技术应用于ML问题。著名的例子包括量子神经网络和量子感知器的开创性研究(Lewenstein,1994; Kak,1995),以及量子计算学习理论的潜力(Bshouty和Jackson,1998)。一直以来,量子神经网络(量子神经网络)一直在持续发展,探讨有关量子力学和神经网络相互作用的各种类型的问题。该领域的大多数研究并非直接针对算法改进,因此在此仅作简要介绍。量子神经网络研究的一小部分在早期活跃得多,它考虑了 量子效应在人工和生物学神经网络中的功能性推测(Kak,1995; Penrose,1989)。该研究路线的一部分集中在具体的模型上,例如HNs中的横向场效应(Nishimori和Nonomura,1996),以及生物网络模型的退相干(Tegmark,2000),据认为这会破坏任何潜量子效应量子效应在的可能性。贯穿量子神经网络研究的第二个主题涉及 对标准前馈神经网络进行有意义的量化的基本问题 。 这里的关键问题是 找到调和量子理论线性性质的最佳方法,以及神经网络激活函数中非线性的必要性(请参阅第II.A.1节),并确定合适的物理系统来实现 这样的策略。这里的早期思想包括放弃非线性本身,并考虑替代神经元层的单层网络(Lewenstein,1994)。另一种方法是利用源自测量和后期选择的非线性(可以说是最早提出的(Kak,1995))。Behrman等人也解决了同样的问题。 (Behrman等,1996)通过使用连续的机械系统,其中通过在量子点的模型系统中通过将系统与环境耦合来实现非线性。对此类网络的实现进行纯粹的基础研究以及对 其量子力学特征的分析一直是并且正在继续成为活跃的研究领域(参见例如(Altaisky 等人,2017))。有关此主题的更多信息,请读者参考更多专业的评论(Schuld等,2014b; Garman,2011)。
与具有基本原理的量子神经网络研究不同,研究经典ML问题的量子效应的大部分工作都专门集中在确定性改进上。在这种情况下,量子优势的第一个例子是在量子计算学习理论的背景下提供的,这是下面第一个小节的主题。在第二小节中,我们将调查研究,提出 提高联想记忆能力 的可能性。最后一个小节讨论了解决经典学习算法在计算 运行时间方面的改进 的建议,其中第一个建议已经在2000年代初问世。在这里,我们将区分通过量子优化在分类器训练阶段侧重于量子改进的方法(主要侧重于利用近期技术和受限设备),以及大致基于 量子并行性 构建算法的方法和“量子线性代数”。通常假设使用通用量子计算机,并且通常是“预填充”数据库。 应该注意的是,量子ML的大部分研究都恰好集中在最后一个方面,这里的结果已经相当多了。 因此,我们只能提出选择的结果。
A. 学习效率的提高:样本复杂性(Learning efficiency improvements: sample complexity)
执行摘要:最初的结果表明,量子计算机和经典计算机之间的分离是在oracles的背景下获得的,并且 样本复杂度高——甚至著名的Grover的搜索算法也构成了这样的结果。同样,CLT处理学习,即概念的识别或近似,这些也不过是oracle。因此,量子非球面计算设置和学习理论共享相同的基础框架,本主题对此进行了研究和应用。为了谈论量子CLT以及对样本复杂度的改进或界限,经典概念预测因此被升级为量子概念预测,其 输出量子状态和/或允许以重叠方式访问。
如第II.B.1节所述,CLT处理学习概念的问题,该概念通常从输入中抽象为长度为n的位字符串的布尔函数,因此c:{0,1} n→{0,1} 单独的输出关系。出于直观目的,考虑光学字符识别(OCR)的任务会有所帮助,在该任务中,我们获得了大小为n = N×M的位图图像(黑白扫描),并且一个概念可以说是“ 代表字母“ A”的所有内容,更确切地说是概念,指定哪些位图对应于字母“ A”的位图。此外,我们在一组概念的学习表现中最有趣的是:概念族C = {c|c : {0,1}n →{0,1}}–在当前的OCR示例中,我们关注的是能够识别所有字母而不仅仅是“ A”的算法。
文献中研究的三个典型设置是PAC模型,从成员资格查询中精确学习以及不可知论模型,请参阅第II.B.1节。 这些模型的不同之处在于可以访问概念Oracle。在PAC模型中,oracle根据某些指定的分布输出带标签的示例,类似于基本的监督学习。在成员资格查询模型中,学习者可以选择示例,这类似于主动监督学习。在不可知模型中,该概念是“嘈杂的”,即形成一种随机函数,在有监督的设置中很自然(联合数据点-标签分布P(x,y)不必起作用),有关详细信息,请读者参考。 第II.B.1节。
1. 量子PAC学习( Quantum PAC learning)
(Bshouty and Jackson,1998)提出了PAC学习的第一个量子概括,其中将量子示例oracle定义为输出相干叠加 a.无分布学习的PAC( Distribution-free PAC) 尽管均匀分布D的假设构成了方便的理论设置,但实际上,大多数情况下,我们对示例的基本分布几乎没有保证。因此,PAC学习通常指的是无分布学习,即最坏情况下的分布D下的学习。也许令人惊讶的是,最近发现,量子PAC学习模型在样本复杂性方面没有经典模型优势。具体而言,在(Arunachalam和de Wolf,2016年)中,作者表明,如果C是VC维数d + 1的概念类,则对于每个(非负)δ≤1/2和≤1/20,每个( ,δ)-量子PAC学习器需要Ω(d / + log(d-1)/)个样本。但是,对于经典的PAC学习器(任意和δ),也可以获取相同数量的样本。(Arunachalam and de Wolf,2016)也证明了类似的结果,表明量子和经典不可知论学习之间没有分离。 b. 量子预测PAC学习(Quantum predictive PAC learning ) 标准PAC学习设置不允许经典和量子样本的学习复杂度之间呈指数分隔,因此,在经典和量子情况下,可学习的概念相同。如果我们考虑较弱的学习环境,或者说学习意义较弱,这种情况就会改变。 PAC学习设置假定学习算法输出的假设h具有 较高的置信度,且误差较小。在经典情况下,期望假设h可以应用一次或任意次数都没有区别。但是,在量子情况下,oracle 中的例子可能是量子状态,这种情况会发生变化,并且通常不可能在所有设置中都进行归纳学习,请参阅第V节。在(加文斯基,2012年)中,作者考虑了一种量子PAC设置,其中只需要一个(或很少数量的)假说评估,即所谓的 预测量子(PQ) 模型。在这种情况下,作者确定了一个关系概念类(即,每个数据点可能具有许多正确的标签),在经典情况下,该概念类不是(多项式)可学习的,但是在标准量子oracle 及均匀分布情况下是可学习的。基本思想是为 每个测试实例使用通过处理量子示例获得的量子状态- 换句话说,假设的“实现”包含从oracle 获得的量子状态。不能有效地估计该量子态,但是可以使用PQ oracle有效地获得。 概念类和标记过程的灵感来自于分布式计算问题,早在(Bar-Yossef等人,2008)中就已经确定了 指数经典量子分离。这项工作为QIP各个方面(在本例中为量子通信复杂性理论)与量子学习之间的紧密联系提供了另一个值得注意的例子。 在从成员资格查询进行精确学习的模型中,学习者可以从希望标记的概念域中选择元素(类似于主动学习),但是,任务是要准确地识别概念(无错误),除了概率δ< 1/390在量子域中,从成员资格查询中学习通常被称为 oracle身份识别 。虽然在这种情况下可以进行量子改进,但在(Servedio和Gortler,2004年)中,作者表明,在大多数情况下,它们最多是低阶多项式改进。更准确地说,如果n位上的概念类C分别具有经典和量子成员资格查询复杂度D(C)和Q(C),则D(C)= O(nQ(C)3)–换句话说,样本复杂度的提高最多可以是多项式。还针对最坏情况的精确学习样本复杂性(所谓的(N,M)查询复杂性)建立了多项式关系,请参阅(Kothari,2013)和(Arunachalam and de Wolf,2017)。以上结果与(Beals等人,2001)的早期结果在本质上相似,在该结果中,除非对Oracle施加结构性承诺,否则量子查询复杂性无法提供比经典结果更好的多项式改进。 迄今为止考虑的结果是经典学习设置的标准,相对简单的概括,导致样本复杂度的提高受到一定限制。如果考虑到计算(时间)复杂性,或者考虑到学习模型的稍微非标准的概括,则可能会有更大的改进。请注意,我们并未明确将计算复杂性分离带入图片。 相反,在假设某些计算问题对学习者来说很难的情况下,我们获得了样本复杂度分离。 特别是,在(Kearns and Valiant,1994)中,作者已经在无分布模型中构造了几类布尔函数,其有效学习(在样本复杂度意义上)暗示了所谓的 Blum整数分解 的能力-a 众所周知,经典任务无法解决,但可以在量子计算机上解决。使用此观察结果,Servedio和Gortler证明了可以从量子PAC进行有效学习的类,以及在量子隶属关系查询模型中可以有效学习的类,但是在相应的经典模型中不能进行有效学习的类,除非可以对Blum整数在一台经典计算机上进行有效分解。 (Servedio和Gortler,2004年)。 执行摘要:关于 量子系统的完整描述通常需要指定成倍数量的复数值振幅的观察结果,导致了这样的想法,即仅使用 对数量稀少的系统就可以使用相同的振幅来存储数据。尽管这种想法在大多数应用中失败了,但它启发了一些最初的建议,即 使用量子系统来显着提高关联或内容可寻址存储器的容量。但是,CAM存储器更可能的量子升级可能来自不同的方向-探索用作CAM存储器的从HN提取信息的方法-并受到量子绝热计算的启发,以实现相似但又不同的标准召回过程。量子方法可以通过输出数据的叠加来产生优势,并且已经表明它们还可以更有效地利用存储器,从而提高容量。 在CLT,NN和QIP之间的领域中的开创性研究挑战了经典的样本复杂性界限。 此后不久(可能是独立地),提出了第一个建议,即 在空间复杂性的背景下改善量子的提议,特别是联想记忆的效率。关联或内容可寻址的存储器(简称CAM)是一种可以加载模式的存储设备,通常是n位位串的子集P = {xi} i,xi∈{0,1} n, 然后,与标准RAM类型的存储器不同,它们不是通过地址而是通过内容相似来恢复的:给定输入字符串y∈{0,1} n,如果存储器是存储的模式之一,则存储器应返回y (即y∈P),或相对于某个距离(通常是汉明距离)与y“最接近”的存储模式。确定性地完美存储任何模式集显然需要O(n×2n)位(共有2n个不同的模式,每个模式都需要n位),而CAM的有趣方面是在稍微放松要求时开始的。 我们可以大致识别出两个基本的想法组,它们被认为可以提高能力。接下来概述的第一组 直接依赖于希尔伯特空间的结构,而第二组思想源于 对CAM存储系统的一个公认架构的量化:Hopfield网络。 在一些第一批作品中(Ventura和Martinez,2000; Trugenberger,2001),有人提出了描述量子位系统的众所周知的“指数大小”希尔伯特空间可能允许指数改进:直观地,甚至指数形式的众多模式集P都可以“存储”。 在仅n个量子位的量子状态下:|ψPi= | P | −12Px∈P| xi。 这些早期的作品提出了关于如何使用这种存储器来恢复模式的创造性想法(例如,通过修改后的幅度放大),尽管这常常是由于缺乏可扩展性而引起的,以及其他一些非常根本的问题,从而无法得出完整的建议,因此,我们将不予探讨细节。 但是,我们将指出,可以解释这些工作,以提出经典数据“幅度编码”的第一个示例,该示例在现代量子ML方法中大量使用。 特别是,CAM的存储内存始终可以表示为单个位串(b(0···0),b(0···1)…,b(1 … 1)) 长度为2n的字节(位串中的每个位都由一个模式索引,并且其值是否被编码)。 因此,该数据矢量(在这种情况下是二进制的,但这不是关键的)被编码为量子位数呈指数形式减小的量子状态的幅度:b =(b(0···0),b(0·· ·1)…,b(1 … 1))→Px∈{0,1} n bx | xi(直到归一化)。 增加CAM存储器容量的一种不同方法是对经典HN的不同方面进行“量化”,这些方面构成了众所周知的经典CAM系统。 a. Hopfield网络作为内容可寻址的存储器(Hopfield networks as a content-addressable memory ) HN是具有一组n个神经元特征的递归NN,其连通性由权重(通常是对称的)实数矩阵W = (wij)ij 和(实际)局部阈值{θi} n i = 1的向量给出。 在CAM存储器的情况下,矩阵W对存储的模式进行编码,在此设置中最好将其表示为符号序列,因此x∈{1,-1} n。给定输入模式y∈{1,−1} n,通过将第k个神经元sk设置为输入模式yk的第k个值,然后按照标准感知器规则进行“网络运行”来实现检索: 每个神经元k通过检查其输入加权和是否在局部阈值之上来计算其后续值:sk←sign(Pl wklsl-θk)(假定sign(0)= +1)。如前所述,在适度的假设下,所描述的动力学系统收敛于局部吸引点,该局部吸引点也对应于伊辛函数的能量最小值: 历史上第一个规则,即 Hebbian规则,满足上述所有条件,并由一个简单的递归关系给出:对于{xk} k组模式,权重矩阵由wij = Pk xk i xk j / M给出。其中xk j是第k个样式的第j个符号,M是样式数。已经从各种角度研究了标准召回和赫比更新下的HN的容量,并且在绝对容量的情况下(随着网络规模的增加,可以无错误存储的模式数量与神经元数量的渐近比 到无穷大),它的标度定为O(n 2ln(n))。 该领域的一个众所周知的结果将其改进为O(n√2ln(n))的容量,并通过Storkey引入了不同的规则来实现(Storkey,1997),同时保持了所有所需的属性。在这里,我们应该强调,广义上讲,容量通常是n中的(亚)线性。 但是,如果放弃某些假设a)、c),则可以在经典设置中获得更好的结果,但这是不理想的。 b.基于Hopfield的CAM的量化( Quantization of Hopfield-based CAMs ) 在早期工作中(Rigatos和Tzafestas,2006年,2007年),作者考虑了模糊的概率学习规则,并广泛地认为:a)此类概率规则与量子思考过程相对应,并且b)所得的CAM可以具有显着更大的 能力。 但是,通过 将HN与绝热QC的思想相结合,最近显示出了更加严格的(并得到了充分解决)的结果。(Neigovzen 等人,2009)提出的第一个想法是 将HN和量子退火联系起来。 回想一下,HN可以用Ising函数(参见等式2)来表征,其中存储的模式对应于局部最小值,并且在不失一般性的前提下,假设局部阈值为零。经典召回对应于寻找最接近输入模式y的局部最小值的问题。 但是,如果添加输入模式代替局部阈值,则会获得具有类似功能的替代系统: 关于近期研究的可实现性,在(Santra等人,2016年)中,作者研究了基于Chimera图的D-Wave可编程量子退火设备的架构对量子召回HN任务的适用性,显示了在近乎可证明的量子改进方面的潜力设备。 执行摘要:量子算法理论为决策问题,各种功能问题,预测问题,采样任务和优化问题提供了计算速度提升的示例。本节介绍了可加快学习速度的量子算法。在底层计算体系结构中,主要有两种方法:一类算法依赖于 量子退火器,这对于QC可能不是通用的,但可以自然地解决在ML上下文中重要的某些子任务。然后,这些方法具有利用近期设备实现的可能性增加。相比之下,第二类方法假定使用 通用量子计算机,并且通常在量子数据库中准备和访问数据,但 需要进行指数级的改进。在这里,我们区分了 量子幅度放大和幅度编码方法,它们几乎没有例外,涵盖了所有用于监督学习和无监督学习的量子算法。 过去几年中,量子ML领域中最有效的研究领域集中在 识别ML算法或其计算密集型子例程 上,这些算法可能会使用量子计算机加速。尽管有多种自然方法可以对已完成的研究进行分类,但是有吸引力的一阶描述遵循的是假设量子计算架构的类型。在这里,我们可以确定专注于使用 量子退火体系结构 的研究,该体系在实验上是合理的,甚至在最近一段时间都可以通过商业途径获得(主要是在D-Wave系统设置方面)。在大多数此类研究中,退火体系结构将用于执行通常在许多经典算法的训练阶段中出现的经典困难优化问题。这种方法涉及的部分通常是将这种ML优化有意义地改写为退火体系结构可以(可能)处理的形式。尽管总体监督任务包括多个计算元素,但在这些建议中,量子系统只会处理优化问题。 加快ML算法的第二种方法假定了通用量子计算功能。在此,通常 以量子电路来表示所获得的算法。对于该研究领域中的大多数研究,为了保证实际的提速,将有其他假设。例如,大多数建议只能保证如果要分析的数据已经存在于一种量子预言机或量子存储器中,并且更普遍地,某些依赖于数据的量子状态,则可以保证有效地改进。首先不计算初始化此类内存的开销,但这可能并非不切实际,因为实际上,同一数据库最常用于大量分析。其他假设也可以放在数据集本身的结构上,例如某些包含数据的矩阵的低条件数(Aaronson,2015年)。 量子优化技术在量子ML中扮演着越来越重要的角色。 在这里,我们可以大致区分两种方法,这两种方法在绝热方法处理经典模型训练的计算难点方面有所不同。在(历史上)第一种方法中,我们在二进制分类器的上下文中处理明确的优化,更具体地说,是在 增强处理(请参阅II.A.3)。从那以后,已经显示出 退火器还可以通过从难以模拟的分布中生成样本来提供帮助。我们将主要关注历史上的第一种方法,仅简要提及其他最近的研究结果。 a.加速优化( Optimization for boosing ) 代表性的研究方向也开始了基于绝热量子计算的量子增强ML的开发,其研究重点是特定的一系列优化问题,称为形式为 由实矩阵J指定的二次无约束优化(QUBO)的问题 换句话说,在ML算法中发生的任何优化方面都可以有效映射到QUBO问题的(非平凡的)实例,尤其是可以通过实验设置实现的那些方面,都是进行量子改进的最佳候选者。这种优化问题已经在很多情况下被发现,主要涉及 训练二进制分类器,因此属于监督学习问题。第一个设置考虑了通过简单假设函数的线性组合构建最佳分类器的问题,该模型将经验误差最小化,同时通过所谓的正则化项控制模型的复杂性。这是升压的常见优化设置(请参阅II.A.3),并且通过适当的数学公式推导和少量假设,可以将其简化为QUBO问题。 通过结合较少的假设,可以在训练二元分类器的背景下表达这一作品的总体背景。对于此设置,考虑数据集D = {xi,yi} M i = 1,xi∈Rn,yi∈{-1,1},以及一组假设{hj} K j = 1,hj:Rn→{ -1,1}。对于给定的权重向量w∈Rn,我们定义hcw(x)= sign(Σk wkhk(x))形式的复合分类器。 复合分类器的训练是通过向量w的优化实现的,以最大程度地减少训练集上的错误分类,并降低过拟合的风险。错误分类成本是通过损失函数L(取决于数据集)和在提升上下文中设置的假设指定的。过拟合的风险由所谓的正则化项R控制。 L和R有一些合理的选择,导致分类器具有不同的属性。通常,最佳选择(其定义取决于上下文)会导致难以优化(Long和Servedio,2010年),其中一些可以简化为QUBO,但并非直接如此。 在有关该主题的开创性论文(Neven等,2008)中,Neven及其合著者考虑了加速设置。选择正则项与0范数成正比,0范数计算非零条目的数量,即R(w,λ)=λkwk0。参数λ控制总体优化任务中正则化的相对重要性。损耗函数的常见选择是0-1损耗函数L0-1,在某些设置下最佳,给出 虽然已知L0-1损失函数是不错的选择,但由于它们会导致非凸优化,因此它们在实践中并不常见-因此,凸函数是首选。但是,在2010年,越来越明显的是 凸函数被证明是错误的选择。例如,在开创性的论文(Long和Servedio,2010年)中,Long和Servedio105表明,在噪声环境中,采用凸优化的增强完全失败。受此启发(Denchev等人,2012),作者重新研究了D-Wave类型的体系结构,并确定了允许进行非凸优化的简化方案。用超平面分类设置表示(如所解释的,这等效于结构中的提升设置),它们标识一个减少量,该减少量(间接)实现了非凸函数lq(x)= min {(1- q)²,( max(0,1-x))²}。此函数称为 q损失函数,其中q是实参。q损失函数的实现允许实现相对于总损失的优化 其细节超出了本文的讨论范围,但我们至少可以解决这个问题。 在校正增强中,该算法每次基本上一次更新权重。在完全校正的提升中,在提升算法优化的第t步,同时更新w的t个条目。众所周知,这会导致更好的正则化解决方案,但优化难度更大。 基数惩罚涉及将0范数明确地用于正则化(前面讨论过),而不是更常见的1范数。同样,这也导致了更难的优化,可以使用退火架构对其进行处理。在(Babbush et al。,2014)中,作者观察到 任何多项式无约束二进制优化都可以以较小的开销映射到(略大的)QUBO上,从而显着概括了可以嵌入量子体系结构的损失函数的范围 问题。这尤其为实现非凸的奇数多项式提供了可能性,这些奇数多项式可以逼近0-1损失函数。 这种方法引入了新的异常但有希望的损失函数类。 b. 量子加速的应用(Applications of quantum boosting) 在(Pudenz和Lidar,2013)的上述“量子增强”架构的基础上,作者探索了(除了增强之外)实现 异常检测 的可能性,特别是在计算验证和验证的计算难题中预见到的。在建议的学习步骤中,作者使用量子优化(增强)功能来学习所测试程序的特性。在新颖的测试步骤中,作者 修改了目标哈密顿量,以降低对输入和输出进行编码的状态的能量,而真实和理想的软件则有所不同。然后可以在叠层绝热召回的背景下,像前面提到的建议一样,以叠加的方式准备这些叠加(即,它们可以准备在输入上叠加的状态,P将产生错误的输出)(Neigovzen等人, (2009年)。 c. 超越增强提升(Beyond boosting ) 除了增强问题外,退火器还被证明对 训练贝叶斯网络结构学习问题 有用(O’Gorman等人,2015),因为他们的训练也可以简化为QUBO。此外,退火架构还可以仅依赖于采样而不是优化 用于深度神经网络的训练。对此的一种值得注意的方法是基于这样一个事实,即对深度网络的训练通常依赖于所谓的生成性深度可信网络,该网络 本质上是多层的受限BM。深度信念网络的训练反过来是计算的瓶颈,因为我需要采样难以生成的分布,这可以使用退火架构更有效地进行准备,请参见例如 (足立和亨德森,2015年)。进一步。 已经提出了引入完全量子BM类模型的新颖思想(Amin等人,2016)。此外,在最近的工作(Sieberer和Lechner,2017)(基于Lechner等人,2015)的灵活构造的基础上,作者展示了如何实现可编程绝热体系结构,该体系结构允许在权重自身重叠的情况下运行算法 。这种可能性也一定会激发出新颖的QML思想。 从BM出发,在最近的工作中(Wittek和Gogolin,2017),作者还展示了 合适的退火架构如何在所谓的马尔可夫逻辑网络中加速概率推理的执行。此任务涉及对统计模型(具体而言是包括伊辛模型)的统计模型(具体是马尔可夫随机场)产生的分区函数的估计。 量子退火可以加速该子任务。 更一般地讲,在退火算法之外的地方,人们开始探索限制,甚至简单的量子系统(可以用当前技术实现)的想法,这些想法可以实现对监督学习有用的信息处理元素。例如,在(Schuld等人,2017)中,一个 简单的干涉电路被用于有效评估数据向量之间的距离,这对于分类和聚类很有用。这些最新想法的更完整说明超出了本文的范围。 ML最近最重要的应用之一是在 数据挖掘 和所谓的 大数据分析 方面。通过提出解决特定ML问题的专用量子算法,已经在此方面取得了最令人印象深刻的改进。这样的算法假定了成熟的量子计算机的可用性,并且自2000年代初以来就被初步地进行了探索。但是,在最近一段时间,我们目睹了大量的想法。 与我们在量子退火的情况下看到的情况不同,在量子退火的情况下,优化子例程仅在量子系统上运行,在本节的大多数方法中,整个算法甚至数据集都可以进行量化。 ML的量子增强思想大致可分为两类:a)依靠Grover的搜索和幅度放大来获得高达二次速度的方法,以及b)将相关信息编码为量子幅度的方法 ,并且有可能实现指数级的改进。第二组方法可能构成了量子ML中最发达的研究路线,并收集了用于量子ML提案的大量量子工具-最著名的是***量子线性代数***。 a.通过幅度放大来加速(Speed-ups by amplitude amplification ) 在(Anguita 等人,2003)中,注意到支持向量机的训练可能是一项艰巨的优化任务,没有比蛮力搜索更好的方法了。反过来,对于没有结构的这种优化情况,QIP至少会以Grover(Grover,1996)搜索算法的变体或将其应用于最小查找的方式得到二次改进(Durr and Hoyer,1999)。这个想法早于并在本质上类似于上一小节中基于绝热的早期提议,但该方法实质上是不同的。在无监督的学习任务的背景下,更广泛地探索了类似Grover的搜索机制所带来的二次改进的潜力(Aèmeur等人,2013)。在这里,作者假设可以访问黑匣子Oracle,该Oracle可以计算任意两个数据点之间的距离度量。 使用这种方法,结合振幅放大技术(例如,最小发现(Durr和Hoyer,1999)),作者在聚类(无监督学习)任务中使用的关键子程序实现了二次改进。具体而言,在执行最小生成树聚类,除法聚类和k中值聚类的算法中获得了改进。此外,这组作者还表明,通过构建Grover搜索的分布式版本,量子效应可以更好地并行化聚类任务。由于经常可以使用大型数据库的分布,因此这种构造可能特别重要。 最近,在(Wiebe等人,2014a)中,作者考虑了训练深层(超过两层)BM的问题。正如我们前面提到的,精确训练BM的瓶颈之一是因为它需要估计某些均衡分布的概率。通常无法进行分析计算(这与计算分区函数一样困难),并且采样方法的成本很高,因为它需要获得平衡分布和多次迭代才能可靠地估计较小的值。通常通过使用代理解决方案(例如,依赖于对比发散)来规避大约训练,但是已知这些方法不如精确训练。在(Wiebe et al。,2014a)中,设计了一种量子算法,该算法***依靠量子幅度放大来准备目标分布的相干编码,从而经常使训练点的数量得到二次改进***,在某些情况下,甚至使神经元的数量呈指数增长。在纯数据挖掘环境中,特别是在关联规则挖掘中,也获得了二次改进(Yu等,2016),粗略地讲,它可以识别大型数据库中对象之间的相关性。作为依赖振幅放大的量子算法一类的最后例子,我们提到了用于训练感知器的算法(Wiebe等,2016)。在这里,量子幅度放大被用于二次加速训练,但是,有趣的是,也被二次减小误差概率。由于感知器构成了SVM的特殊情况,因此该结果在动机上与更老的提议相似(Anguita等,2003),但依赖于更现代且涉及更多的技术。 b. 幅度编码的前体 (Precursors of amplitude encoding) 在早期开创性工作中(经常被忽略)(舒茨德,2003年),舒茨德提出了将QC有趣地应用于模式识别问题的方法,该方法解决了许多仅由社区进行研究和重新发明相对较新的想法。 作者考虑了以N×M黑白位图指定的,以函数f为特征的图像中识别“图案”的问题:{1,…,N}×{1,…,M} →{{0,1}(在技术上与CLT中的概念相同,请参见II.B.1),指定坐标(x,y)处像素的颜色值f(x,y)∈{0,1} 。 函数f给出为量子oracle | x>| y> | b> Uf→| x> | y> |b⊕f(x,y)>。oracle在量子并行中使用(应用于所有坐标的叠加),并且以位值为1为条件(只要点的密度恒定,该过程以恒定的概率成功进行),导致状态|ψ>= NΣ_(x,y stf(x,y)= 1) | x>| y>,其中N是归一化因子。注意,以计算为基础时,此 状态与矢量化位图图像本身成比例。 接下来,作者指出,通常可以通过将离散傅立叶变换应用于具有经典复杂度O(NM log(NM))的图像矢量来检测“图案”(重复宏观特征)。然而,***量子傅里叶变换(QFT)可以利用指数更少的门应用于状态|ψ>***。作者继续表明,对QFT转换状态的测量可能会产生有用的信息,例如模式定位。 这项工作在某些方面是创新的。首先,作者使用量子存储器将数据点(此处为二进制值的字符串)编码为振幅,其方式与VI.B.1中讨论的内容可寻址存储器的应用有关。 然而,应该指出的是,在振幅编码的当前应用中,非二进制振幅具有明确的含义(在灰度图像中),尽管作者没有明确讨论。其次,与所有先前的建议相反,作者展示了一系列任务可量化的指数计算复杂性改进的潜力。但是,这完全取决于对预填充数据库(Uf)的访问,而预填充数据库的加载将使任何优势失效。除了可以认为是一个开销的事实外,舒茨德(Schutzhold)讨论了一种 以量子并行方式从光学图像加载数据的物理方法,这种方法可能是有效的。 c. 幅度编码:线性代数工具(Amplitude encoding: linear algebra tools ) 幅度编码的最基本思想是 将N级量子系统的状态视为数据向量本身。更准确地说,给定数据向量x∈Rn,幅度编码将构成归一化量子态 |x> =Σi xi|i>/||x||, 通常还假设总是可以访问向量||x||的范数。 注意,将N维数据点编码为n∈O(log(N))个量子位的幅度。因此,应用于n比特寄存器对数据进行编码的任何多项式电路都仅构成相对于数据矢量大小的对数计算,这是所有指数改进的基础(同样在(Schutzhold,2003)的情况下) ,在上一节中讨论)。 这些想法导致了一个可以称为“量子线性代数”(QLA)的研究领域,即 通过直接将数值向量编码为状态向量来解决某些线性代数问题的算法的集合。这些量子子例程随后已用于加速众多ML算法,我们将在本节稍后部分介绍其中的一些算法。QLA包括用于矩阵求逆和主成分分析的算法(Harrow等,2009; Lloyd等,2014),还有许多其他算法。出于教学目的,我们将首先给出最简单的示例,该示例以 对数时间执行内积的估计。 工具1:内积评估: 如果可以访问准备量子态|ψ>和|φ>的盒子,则可以使用O(1 /∈)副本,通过所谓的交换测试,精确估计重叠(1+|<φ|ψ>²) ²。 交换测试(Buhrman等人,2001)将受控SWAP门应用到状态|ψ>|φ>,其中控制量子位设置为均匀叠加| + >。“成功”的概率,即 观察| +>给电路后的控制(1+|<φ|ψ>²) ²。并且可以通过迭代来估计(使用量子相位估计的更有效的选择也是可能的)。如果状态|ψ>和|φ> 编码单位长度数据矢量,则成功值会 将其内积编码为正负号。规范和相位也可以通过对该基本概念的细微调整来估算-特别是,幅度编码状态的实际规范将在单独的oracle中访问,并在算法中使用。此过程的样本复杂度仅取决于精度,而门的复杂度与O(log(N))成正比,因为需要控制交换和测量许多量子位。 如果将简化状态混合在一起,并且总体状态为乘积,则交换测试也可以按预期工作。相对于经典矢量乘法,这种计算内积的方法相对于N(如果对生成|ψ>和|φ>的设备的调用为O(1))具有相对于N的指数级改进,但代价是与 误差,因为经典算法具有典型的误差缩放比例,且误差为对数误差O(log(1 /))。 但是,在ML问题的情况下,这可以构成一个很好的折衷方案。 工具2:量子线性系统求解 ML量子增强算法中最有影响力的技术也许是基于线性代数的一个典型问题:求解方程组。在他们的开创性论文(Harrow等,2009)中,作者提出了用于“量子线性系统”(QLS)求解的第一算法,该算法执行以下操作。考虑一个N×N线性系统Ax = b,其中κ和d是条件数,并且厄米系统矩阵A的稀疏性。给定(量子)的甲骨文给出A的非零元素的位置和值(即给定的标准甲骨文在哈密顿模拟中遇到,请参阅(Berry 等人,2015))和一个准备量子的甲骨文 态| b>是b的幅度编码(直到范数),(Harrow等,2009)中的算法准备了量子态| x>,其近似于解矢量x的幅度编码。第一个算法的运行时间为〜O(κ2d2log(N)/)。 请注意,复杂度与系统大小的对数成正比。请注意,任何经典算法都必须至少以N缩放,这为指数改进提供了更大的空间。(Harrow et al。,2009)中的原始建议依赖于应用相位估计的汉密尔顿模拟(实现exp(iAt))。一旦估计了相位,就可以通过测量来添加反比例的振幅(即A的特征值的倒数)。还已经注意到,某些标准矩阵预处理技术也可以在QLS方案中应用(Clader等,2013)。这些建议中误差的线性缩放源于相位估计子程序。 在最近的工作中(Childs等人,2015年),作者还依赖于最佳的汉密尔顿模拟技术,但放弃了昂贵的相位估计。粗略地说,它们根据输入状态(概率)实现形式为Σkαkexp(ikAt)的单元的线性组合。这构成了aries的多项式,可以使多项式更有效地近似于逆算符A-1(在可访问测量的子空间中)。结合其他众多优化方法,得出了最终算法,其复杂度约为O(κdpolylog(N /)),基本上是最优的。 重要的是要注意,即使我们假定可以自由访问所有预言机,上述显然效率更高的方案也并不意味着可证明的计算改进。例如,问题之一是量子算法输出一个量子状态,经典值只能通过采样来访问。重建完整输出向量的此过程将扼杀任何改进。另一方面,可以有效地计算振幅的某些函数,其计算可能仍然经典地需要O(N)步,从而产生了所需的指数改进。因此,此算法作为子例程,是更大算法(例如用于量子机器学习的算法)的中间步骤,将是最有用的。 工具3:密度矩阵求幂: 密度矩阵幂运算(DME)是一个非常简单的想法,几乎没有什么微妙之处,而且可以说是深刻的后果。考虑N维密度矩阵ρ。现在,从数学的角度来看,ρ只是半正定矩阵,尽管它也常用于表示量子系统的量子状态–这两个是不同的概念。初次阅读,ρ是矩阵(为避免混淆,我们将其表示为[ρ]),[ρ]也是对物理哈密顿量的有效描述,具有时间积分演化exp(-i [ρ] t )。一个近似的exp(-i [ρ] t)可以访问状态为ρ的量子系统吗?给定足够多的副本(ρ⊗n),最明显的答案是肯定的-一个人可以使用全状态层析成像以任意精度重建[ρ],然后使用哈密尔顿模拟(尽管有效率)执行。在(劳埃德等人,2014年)中,作者展示了一种非常简单的方法:给定任何输入状态σ和ρ的一个副本,即量子状态 备注(Remark): 用于QLS,内积评估,量子PCA的算法,因此,本节其余部分中列出的几乎所有量子算法也都采用“预加载的数据库”,从而允许以并行方式访问信息和/或访问或有效访问数据库。 准备振幅编码状态。使用所谓的量子随机存取存储器(qRAM)架构已经解决了并行访问甚至是量子状态存储的问题,并已解决了大多数问题(Giovannetti等,2008)。相同的qRAM结构也可用于实现基于量子搜索的方法中使用的预言。但是,可以使用预先填充有经典数据的量子数据库确实 没有先验 地暗示着也可以有效地生成量子振幅编码状态,这在下面的大多数工作中至少是不正确的。对于一些类似假设的成本的单独讨论,我们请读者参考(Aaronson,2015年)。 d. 幅度编码:算法(Amplitude encoding: algorithms ) 有了所有的量子工具,我们现在可以针对各种有监督和无监督的学习任务,提供按其解决的问题类别分组的量子算法。本节的大多数建议遵循一个清晰的范例:作者研究了已建立的ML方法,并确定了那些 可以将计算量大的部分简化为线性代数问题(最常见的是对角化和/或方程求解)的方法。 从这个意义上讲,量子线性代数方法的进一步改进很可能导致量子ML的新结果。 最后,以下所有算法均与 离散系统 实现有关。 最近,在(Lau等人,2017)中,作者还考虑了qRAM,QLS和DME的连续变量变体,这立即导致了下面列出的所有量子工具和大多数量子增强型ML算法的连续变量实现。 回归算法量子增强的第一个建议是解决线性回归问题,特别是基于QLS的最小二乘拟合。在最小二乘拟合中,我们给N个M维实数数据点与实数标签配对,因此(xi,yi)N i = 1,xi =(xj i)j∈RM,y =(yi)i∈RN。在回归中,y被称为响应变量(也称为回归变量或因变量),而数据点xi被称为预测变量(自变量或回归变量或解释变量),最小二乘线性回归的目标是建立最佳线性模型,即 β=(βj)j∈RM给出 最终结果是在时间O(κ4d3log(N)/)中与解矢量β成比例的量子状态β,其中κ,d和是条件数,即“对称”数据矩阵X†的稀疏性 X和偏差。同样,我们通常对κ的行为几乎没有任何保证,并且对数据矩阵的稀疏性d有明显的限制。 但是,只要两者均为O(polylog(N)),我们就有潜力进行指数改进。由于该算法以量子态编码,因此对于实际找到解矢量β显然没有用。尽管如此,它对于估计拟合量子位还是有用的:从本质上讲,通过将X应用于|β>,我们可以获得y的最终预测值,可以通过交换测试将其与实际响应变量矢量进行有效地比较。 此后,在一些著作中扩展了量子线性回归的这些基本思想。 在广泛而互补的工作中(Wang,2014),作者依靠强大的“量子化”技术(Low和Chuang,2016),并优化了实际生成最佳拟合参数β的目标。根据需要,其算法的复杂度与数据点的数量M成正比,但在数据维度N上是对数的,在其他相关参数上则非常有效。在(Schuld et al。,2016)中,作者更紧密地遵循(Wiebe et al。,2012)的思想,并且当数据矩阵不是稀疏的而是低维度的时,也可以达到与原始工作相同的结果。 此外,它们通过使用其他最新技术改善了复杂性。 后者的工作主要依靠DME技术。 聚类算法(Clustering algorithms ) 在(Lloyd et al。,2013)中,使用幅度编码和内积估计来估计给定数据向量u与数据点集合(质心)的平均值之间的距离ku- vk v = Σi vi / M 对于M个数据点{vi} i,时间在向量长度N和点数M上都是对数的。以此为基础,作者还展示了一种用于 k均值分类/聚类的算法(其中到质心的距离的计算是主要成本),从而实现了总体复杂度O(M log(MN)/) ,在某些情况下甚至可以进一步改善。在这里,假设幅度编码的状态向量及其归一化值可以通过oracle访问,或者可以通过存储所有值的qRAM有效地实现。类似的技术,结合相干量子相位估计和基于Grover的优化,也已用于解决有监督和无监督学习的k最近邻算法问题(Wiebe等人,2015)。 量子主成分分析(Quantum Principal Component Analysis ) DME的想法在同一篇论文中(Lloyd等,2014)立即应用于主成分分析(PCA)的量子版本。 PCA构成了最标准的无监督学习技术之一,对降低维度很有用,当然,除了ML之外,它还具有广泛的应用范围。在量子PCA中,对于一个量子态ρ,人们使用DME将一元exp(-i [ρ])的量子相位估计应用于状态ρ本身。在绝对精度的理想情况下,给定频谱分解ρ= Σiλi|λi><λi|,此过程将生成状态Piλi|λiihλi|⊗|〜λiih〜λi|,其中〜λi表示特征值λi的数值估计 到特征向量|λii。 从该状态采样将同时恢复(较大的)特征值和相应的量子状态,这些量子状态对特征向量进行幅度编码,可以在其他量子算法中使用。高值特征值和特征向量的恢复也构成了经典PCA的本质。 量子支持向量机(Quantum Support Vector Machines) 量子增强ML中最具影响力的论文之一是 依靠QLS和DME来量化支持向量机算法的任务。 有关SVM的基本概念,请参阅第II.A.2节。 我们将注意力集中在训练SVM的问题上,该问题由方程式(6)中的双重形式的优化任务给出。为方便起见在此重复: 作为热身的结果,在(Rebentrost等人,2014)中,作者指出,使用内在产物的量子评估,出现在等式(30)中 ,就数据向量维数N而言,已经可以导致指数级加速。但是,量子算法的复杂度仍然是数据点M的多项式,并且误差相关性现在是线性的(因为内积估计的误差是线性的)。作者继续表明,对于最小二乘SVM的特殊情况,完全指数的改进是可能的(相对于N和M)。 考虑到我们已经针对DME和QLS进行的背景讨论,此处的基本思想很容易解释。回想一下,训练最小二乘SVM的问题简化为线性程序,特别是最小二乘最小化。 如我们先前所见,这种最小化简化为方程式求解,方程式由系统给出。在此重复: 高斯过程回归(Gaussian process regression) 在(Zhao 等人,2015)中,作者演示了如何使用QLS来显着改善高斯过程回归(GPR):一种强大的监督学习方法。GPR可以看作是标准回归的随机概括:给定训练集{xi,yi},它对潜函数建模(将标签y分配给数据点),假设标签上的高斯噪声f(x)= y +编码独立且均匀分布的位置更精确地说,GPR是一个过程,其中使用贝叶斯推理,通过考虑训练设定点来确定可能的潜在函数的初始分布。因此,从广义上讲,GPR的输出是模型f上的分布,该模型与观测数据(训练集)一致。 尽管这种分布的描述可能很大,以计算方式来预测新点x的值,但在GPR中,一个人需要计算两个数字:线性预测变量(也称为 预测均值,或者简称为 均值)和 预测变量的方差,具体针对x。 这些数字表征了GPR模型的预测值y ∗的分布,该分布与训练数据一致。而且,事实证明,两个值都可以使用改进的QLS算法来计算。最终输出大小独立于数据集大小,再加上QLS,这一事实为数据大小的指数加速提供了可能性。 只要数据在qRAM中可用,这自然就成立了,这与本节的大多数算法一样。 应当提到的是,作者在计算复杂度的最后统计中一丝不苟地列出了所有“隐性成本”(以及制定中间算法)。 几何和拓扑数据分析(Geometric and topological data analysis) 到目前为止,我们在本小节中介绍的所有算法都严重依赖于对“预加载”数据库的访问-加载本身会导致对数据库大小的线性依赖,而内积,QLS和DME算法则为对数依赖性。但是,在可以有效地单独计算量子数据库中数据点的情况下,可以避免这种情况。 这使人联想到Grover算法的大多数应用程序都具有有效计算Grover oracle的步骤。在ML应用程序中,如果经典算法要求(相对较小的)数据集进行组合探索(作为计算步骤),则会发生这种情况。然后,量子算法可以在量子并行中生成组合更大的空间,从而有效地计算有效的量子数据库。(Lloyd 等人,2016)在拓扑和几何数据分析的背景下提出了实现此目标的第一个示例。 这些技术在机器学习的背景下非常有前途,因为数据的拓扑特征不取决于选择的度量标准,因此可以捕获数据的真正鲁棒的特征。拓扑特征(在离散数据点的ML世界中)的概念是由在不同空间分辨率下观察数据时存在的那些属性给出的。因此,这样的持久性特征是鲁棒的,并且不太可能是噪声或参数选择的伪像,并且通过所谓的持久性同源性在数学上形式化。感兴趣的特定特征族是连接的组件,孔,空隙(或腔)的数量。这些数字定义为简单复数(大致是一组封闭的单纯形),称为Betti 数。为了从数据中提取此类特征,因此必须从数据构造嵌套的简单复数族,并计算由贝蒂数捕获的相应特征。但是,从组合上讲,应该考虑并应该分析多个简化,并且可以将每个可能的单纯形粗略地认为是需要进一步分析的数据点。但是,它们是从一小组有效地生成的-本质上是数据点之间成对距离的集合。作者展示了 如何生成以对数个量子位为单位对单纯形进行编码的量子态,并进一步表明,根据这种表示,可以有效地估计Betti数。在各种分辨率下进行迭代可以识别持久性特征。像往常一样,在数据的某些假设下会发生完全指数式的改进,在这里,它们表现为有效构造简单状态的能力–特别是,复杂系统中单纯形的总数将成倍增长,尽管尚不清楚这种情况,请参阅(Aaronson,2015)。该提议提供了证据,即即使没有将数据预先存储在qRAM或类似系统中,基于幅度编码的量子ML方法也可能至少在某些情况下产生指数级的加速。 如前所述,现代方法是量子增强ML的重要组成部分,它依赖于量子线性代数技术,并且该领域的任何进展都可能导致新的量子ML算法。关于量子梯度下降的算法(Rebentrost et al。,2016b; Kerenidis and Prakash,2017),给出了一个有前途的例子。 导致了用于训练神经网络的新型量子方法。

对于概念c,对于数据点x上的给定分布D。 回想一下,经典的PAC oracle输出一个样本对(x,c(x)),其中x是从D提取的,这可以理解为混合状态的副本Px pD(x)| x,c(x)ihx,c( x)|,其中pD(x)= P(D = x)。如果量子示例是在标准(计算)基础上测量的,则量子先知会简化为标准先知。第一项开创性工作表明,量子算法可以访问这样的量子广义化的预言系统,从而可以提供对某些概念类的更有效的学习。作者考虑了 均匀分布下的DNF 公式的概念类别:这里的概念是析取正态形式的s项公式。换句话说,每个概念c的形式为c(x)= WIVj(xI)0 j,其中xI是与I相关联的x的子字符串,它是最多s的基数索引的子集,并且(xI )0 j是一个变量或其取反(文字)。 DNF的示例形式为(x1 x3 x3 x6)∨(x4 x8 x8 x1)···, 所有的括号都是不相交的(OR,∨)。尚不知道统一的DNF学习问题(对于n个变量和poly(n)项)可以有效地实现PAC的学习,但是在(Bshouty and Jackson,1998)中被证明可以有效地实现量子PAC的学习。选择此学习问题并非偶然:在成员资格查询模型中已知DNF学习是可学习的,下一节将对此进行详细描述。 在隶属关系查询模型中学习DNF的相应经典算法直接启发了PAC案例中的量子变体。如果概念域上的基础分布是均匀的,那么其他概念类也可以通过量子加速来学习,特别是所谓的k-juntas:n位二进制函数,仅依赖于k 2. 从会员查询中学习(Learning from membership queries)
B.学习能力的提高(Improvements in learning capacity)
1. 幅度编码的容量(Capacity from amplitude encoding)
2. 通过量化的Hopfield网络的能力( Capacity via quantized Hopfield networks)

在给定要存储一组模式的情况下,这样的系统仍然允许在指定矩阵W的规则中有很大的自由度:直观地,我们需要“编程” E的最小值(选择合适的W将成功,因为可以使用局部阈值 设置为零)作为目标模式,理想情况下不会存储太多不需要的,所谓的虚假模式。这以及有用的存储规则的其他属性,即 给定模式的W的规则,如下所示(Storkey,1997):a)位置:特定连接的更新应仅取决于可用于 连接两侧的神经元; b)增量性:该规则应允许矩阵W的更新仅基于新模式和W本身来存储其他模式;c)即时性:该规则不应要求用于评估权重矩阵的限制性计算过程( 相反,它应该是几个步骤的简单计算)。有用规则的最关键属性是d)导致CAM具有不平凡的容量:它应该能够存储和检索一定数量的图案,并且错误率具有可控制性(例如,包括很少的虚假模式) 。
直观地讲,这特别在输入模式配置周围降低了系统的能量分布。但是,然后,最接近输入模式的存储模式(先前的局部最小值)最有可能成为全局最小值。 此外,现在可以通过量子退火解决发现这些配置的问题:我们自然地将量子“记忆哈密顿量”定义为

和HN哈密顿量,给定输入y,Hp = Hmem +ΓHinp,其中输入哈密顿量为
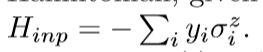
通过哈密顿轨迹H(t)=Λ(t)Hinit + Hp通过绝热演化获得量子召回,其中Λ(0)足够大,以Hinit为主,而Λ(1)=0。系统初始化 在(任意且简单的)哈密顿量Hinit的基态下,如果t的演化慢到足以 满足绝热定理的标准,则系统以Hp的基态结束。该建议将局部优化(经典检索)转化为全局优化。 虽然这通常不是一个好主意,但所获得的是可以在绝热体系结构上运行的问题的量子公式,以及以下事实:如果多个存储的模式近似相等,则该系统可以返回召回模式的量子叠加输入,这可能是一个优势(Neigovzen等,2009)。但是,上述系统的行为与经典召回网络并不完全相同,后者在随后的工作(Seddiqi和Humble,2014)中进行了进一步研究,分析了各种经典学习规则下量子召回的敏感性。此外,在(Santra等人,2016)中,作者对基于Hebb的HN的容量进行了广泛的分析,但是在(Neigovzen等人,2009)提出的量子退火召回下,令人惊讶的是,这 在随机存储器的假设下,模型产生指数存储容量。 这一结果与教科书中报告的标准古典能力形成了鲜明的对比。C. 运行时间的改进:计算复杂性( Run-time improvements: computational complexity)
1. 通过模拟退火优化加速(Speed-up via adiabatic optimization)

只要我们不对基础晶格做任何假设,QUBO问题等同于识别Ising函数的最低能量状态的问题:

现代退火架构提供了利用绝热量子计算解决此类基态问题的手段。通常,我们正在处理的系统可以实现H(t)形式的可调哈密顿量

其中A,B是光滑的正函数,使得A(0)》B(0)和B(1)》A(1),即通过缓慢地缓慢调整t,我们可以进行绝热准备基态 伊辛哈密顿量 H_target,从而解决了优化问题。实际上,参数Jij不能完全自由选择(例如,连通性仅限于D-Wave体系结构中的所谓的Chimera图(Hen等人,2015)),而且实现的交互强度值的精度 和准确性也有限。(Neven等,2009a; Bian等,2010),但我们暂时将其忽略。通常,找到 Ising模型的基态 是功能性NP难题,这很可能超出了量子计算机的范围。然而,退火架构仍然可以具有许多优点,例如,据信它们仍可以在所有情况下或至少在平均情况下提供提速,和/或它们可以提供良好的启发式方法,并希望接近最佳解决方案。
![]()
这恰好构成了标准的提升框架,但也与某些SVM(即超平面分类器)的训练密切相关。换句话说,用于提升设定的量子优化技术也可以帮助超平面分类。
![]()
(其中Θ是阶跃函数),它仅计算错误分类的次数。 就性能而言,此选择动机良好,但可能很难进行计算。 作者认为,权重w的适当离散化可能不会影响性能,因此上述方法构成了一般绝热方法的可靠候选者。但是,它不适合QUBO结构(仅具有二次项),因此无法使用现有体系结构解决。为了获得所需的QUBO结构,作者施加了两种修改:他们选择了二次损失函数

可以在一定程度上规避)。 还使用数值实验测试了这种系统。 在后续论文中(Neven等,2009a),同一团队对初始建议进行了概括,以适应另一个实际问题:问题规模。可用的体系结构允许对数千个变量进行优化,而实际上,对(K)进行优化的假设数量可能会大得多。为了解决这个问题,作者展示了如何在维持(通过实验验证)良好性能的同时,将较大的优化问题分解为更易于管理的部分。 这些想法也在实际的物理体系结构中进行了测试(Neven等,2009b),并在更一般的迭代算法中进行了组合和完善(Neven等,2012),也使用了实际的量子体系结构进行了测试。

在这种情况下,所得的正则化项与w的2范数成正比,而不是与先前示例中的0范数成正比,后者可能不是最优的。尽管如此,以上内容还是一个典型的例子,其中量子体系结构导致了ML设置,这在经典情况下是不会被探索的(损耗Lq在许多情况下不太可能自然出现),并且动机很好,因为:a)不是凸函数,因此有可能规避凸函数的所有不合格结果,并且b)优化过程可以在物理系统中实现。作者进行了许多数值实验,证明了在分析噪声数据时选择非凸损失函数的优势,这肯定是有希望的。在后来的工作中(Denchev等人,2015),还提出了在量子架构中可以实现的损耗正则化的组合也可以用于所谓的完全校正性的基数罚分增强,这被认为是经典难以处理的 。2. 加快电路架构(Speed-ups in circuit architectures)
![]()
其中S是对应于量子SWAP门的Hermitian算子,将所需的时间演化近似为一阶
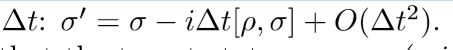
如果重复此过程,则通过使用ρ的新副本,我们可以通过将∆t设置为O(∈/ t)来获得目标状态σρ= exp(-iρt)σexp(iρt)可以近似为精确∈。 使用状态ρ的O(t2 /∈)副本。从某种意义上讲,DME是在两个量子态之间使用SWAP测试来模拟由一个量子态指定的测量方面的过程的概括。这一结果的直接结果是在哈密顿模拟的背景下, 只要能够以哈密顿矩阵表示的状态制备量子系统,就可以有效地实现哈密顿模拟(而不依赖于哈密顿稀疏性) 。 尤其是,只要哈密顿量本身是低阶的,就可以使用qRAM存储的哈密顿量描述来实现。 更一般地,这还意味着 当系统矩阵不是稀疏而是由很少的主成分(即接近低秩矩阵)控制时,也可以有效地执行QLS算法。

其中,数据矩阵X的行表示每个数据点的特征属性。换句话说,线性回归假设预测变量(自变量)和响应变量(因变量)之间存在线性关系。众所周知,上述最小二乘问题的解由β= X + y给出,其中X +是数据矩阵的Moore-Penrose伪逆,即在X†X是可逆的情况下 ,由X + =(X†X)-1X†给出。(Wiebe et al。,2012)的基本思想是将X†应用于初始向量| y>,该向量对响应变量进行幅度编码,从而获得与X†| y>成比例的状态。 这可以完成 通过修改原始的QLS算法(Harrow等人,2009年),不仅可以输出特征值的倒数,还可以输出特征值本身。此后,将(X†X)-1(应用于与X†| yi成比例的生成状态)的任务解释为系统(X†X)β= X†y的方程求解问题。
![]()
然后可以通过![]() 轻松计算所需SVM的解。
轻松计算所需SVM的解。

在这里,1是“全1”向量,Y是标记yi的向量,α是拉格朗日乘子产生解的向量,b是偏差项,γ是取决于超参数C的参数,而Ω是收集训练向量的(映射的)内积的矩阵,因此Ωi,j = xi.xj。(Rebentrost et al。,2014)的关键技术方面展示了如何以适合QLS的方式实现上述系统。为了使这种方法更好,我们将简单指出系统子矩阵与追寻子系统2之后获得的量子态Σi | xi || i>1 | xi>2的缩减密度矩阵成比例。在某些约束下,可以通过访问对数据点进行编码的qRAM来有效地实现此状态。此后,DME启用了QLS的应用,其中系统矩阵具有与Ω成比例的块,为简洁起见,我们省略了详细的技术细节。总体量子算法生成与![]() 成比例的量子态,并对偏移量和乘数进行编码。 不需要通过采样从该状态中提取乘数。 取而代之的是,可以通过(1)生成输入的幅度编码状态,以及(2)估计此状态与
成比例的量子态,并对偏移量和乘数进行编码。 不需要通过采样从该状态中提取乘数。 取而代之的是,可以通过(1)生成输入的幅度编码状态,以及(2)估计此状态与![]() 之间的内积来对任何新点进行分类。 通过使用|ψouti调用量子数据预言。 该过程的整体复杂度为
之间的内积来对任何新点进行分类。 通过使用|ψouti调用量子数据预言。 该过程的整体复杂度为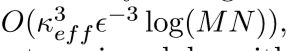 ,其中κeff取决于数据矩阵的本征结构。 只要此术语在数据大小上是多对数的,我们就有可能实现指数级的改进。
,其中κeff取决于数据矩阵的本征结构。 只要此术语在数据大小上是多对数的,我们就有可能实现指数级的改进。