第十四章聚类方法.14.2.5有序样本分类法

本课程来自深度之眼，部分截图来自课程视频以及李航老师的《统计学习方法》第二版。
公式输入请参考： 在线Latex公式

主要内容

算法功能与数据类型：理解算法定义与适⽤样本数据类型
类的直径：每类直径D(i,j)的表达式与数学性质
分类的损失函数：分类损失函数L[b(n,k)]的定义与表达式
最优解的求法：最优分点的确定与迭代过程
损失函数递推公式：递推公式与最优化
案例分析：类间距离计算：运⽤欧⽒距离度量各间距离D(i,j)
案例分析：各类损失函数：计算各分类损失函数
案例分析：最优分割点：查找最⼩损失函数L[P(n,k)]表确定最优分割点

算法功能与数据类型

有序样本（样本的顺序是固定的）聚类法⼜称为最优分段法，由费歇在1958年提出，主要适⽤于样本主要与1个变量有关的问题，或将多变量综合成为单变量变量进⾏分析。
设$\Omega =\{{\bar{\omega }}_1,{\bar{\omega }}_2,\cdots ,{\bar{\omega }}_{\pi }\}$是样本点构成的集合，样本点${\bar{\omega }}_i$在函数$V(\bar{\omega })$上的取值为$V_i$。若$V({\bar{\omega }}_i)=V({\bar{\omega }}_j)$则将视为一类。不妨假设$v_1<v_2<\cdots <v_m$。要将$v_1,v_2,\cdots ,v_m$分为K类：即$P=(P_1,P_2,\cdots ,P_k)$，分类时不能打乱样本点的顺序，即每一类必须呈现$\{{\bar{\omega }}_1,{\bar{\omega }}_2,\cdots ,{\bar{\omega }}_{\pi }\}$的形式，即有序样本聚类。

有序聚类步骤

定义类的直径

设有序样本$x_{(1)},x_{(2)},\cdots ,x_{(n)}$，可按指标数值由小到大排列，也可按时间先后排列。
第一步，看类的大小，先定义类的直径
设某类G中包含的样品有：
$$x_{(i)},x_{(i+1)},\cdots ,x_{(j)},(j>i)$$
该类的均值向量为（所有样本点到重心${\bar{X}}_G$的平均距离）：
$${\bar{X}}_G=\frac{1}{j-i+1}\sum _{t=i}^j{x}_{(t)}$$
用$D(i,j)$表示类的直径，常用的直径有欧氏距离：
$$D(i,j)=\sum _{t=i}^j(x_{(t)}-{\bar{X}}_G{)}^{\prime }(x_{(t)}-{\bar{X}}_G)$$
当数据集是单变量的时候，距离就是一维的，就可以写为：
$$D(i,j)=\sum _{t=i}^j|x_{(t)}-{\bar{X}}_G|$$

定义分类的损失函数

⽤$b(n,k)$表示将$n$个有序的样品分为$k$类的特定分法：
$$\begin{gathered} G_1=\{j_1,j_1+1,\cdots ,j_2-1\} \\ {G}_2=\{j_2,j_2+1,\cdots ,j_3-1\} \\ \cdots \\ {G}_k=\{j_k,j_k+1,\cdots ,n\} \end{gathered}$$
这种分类法的损失函数为各类直径之和：
$$L[b(n,k)]=\sum _{t=1}^{k}D(i_t,i_{t+1}-1)$$
由上面的定义可知损失函数为各类直径之和，数值较⼤则说明分类效果不佳。
当$n$和$k$固定时， $L[b(n,k)]$越小表明各类离差平方和越小，分类合理。
因此需要寻找⼀种分法$b(n,k)$，使分类损失函数$L[b(n,k)]$达到最小值，记该分法为$P[n,k]$。

最优解的求法

若分类数$k$已知，求分类法b(n,k)使在损失函数意义下L[b(n,k)]达到最小，求法如下：
(1)找出分点$j_k$，使分类一分为2，该分法得到损失函数最小
$$P(n,2):\{1,2,\cdots ,j_k-1\},\{j_k,j_k+1,\cdots ,n\}$$
且
$$L[P(n,2)]=\underset{2\le j\le n}{\min }[D(1,j_k-1)+D(j_k,n)]$$
那么从分点到最后一个样本就是第k类：
$$G_k=\{j_k,j_k+1,\cdots ,n\}$$
(2)接下来迭代，找出$j_{k-1}$，使它满足：
$$P(j_k-1,2):\{1,2,\cdots ,j_{k-1}-1\},\{j_{k-1},j_{k-1}+1,\cdots ,j_k-1\}$$
且
$$L[P(j_k-1,2)]=\underset{2\le j\le j_k-1}{\min }[D(1,j_{k-1}-1)+D(j_{k-1},j_k-1)]$$
那么从分点到第$j_k-1$个样本就是第k-1类：
$$G_{k-1}=\{j_{k-1},j_{k-1}+1,\cdots ,j_k-1\}$$
(3)找出$j_{k-2}$，使它满足：
$$P(j_{k-1}-1,2):\{1,2,\cdots ,j_{k-2}-1\},\{j_{k-2},j_{k-2}+1,\cdots ,j_{k-1}-1\}$$
且
$$L[P(j_{k-1}-1,2)]=\underset{2\le j\le j_{k-2}-1}{\min }[D(1,j_{k-2}-1)+D(j_{k-2},j_{k-1}-1)]$$
那么从分点到第$j_{k-1}-1$个样本就是第k-2类：
$$G_{k-2}=\{j_{k-2},j_{k-2}+1,\cdots ,j_{k-1}-1\}$$
依此类推得到所有类：$G_1,G_2,\cdots ,G_k$
(4)$L[b(n,k)]$的递推公式：
$$\{\begin{array}{ll}& L[P(n,2)]=\underset{2\le j\le n}{\min }\{D(1,j-1)+D(j,n)\}\\ & L[P(n,k)]=\underset{k\le j\le n}{\min }\{L[P(j-1,k-1)]+D(j,n)\}\end{array}$$

小结：
求$n$个样品分为$k$个类的最优分割应建立在已将$j-1(j=2,3,...,n)$个样品分为$k-1$个类最优分割的基础上。

例子：

分析⼉童的生长期：资料是1-11岁的男孩平均每年的增重，
求男孩生长发育阶段的合理划分。

年龄	1	2	3	4	5	6	7	8	9	10	11
增重（公斤）	9.3	1.8	1.9	1.7	1.5	1.3	1.4	2.0	1.9	2.3	2.1

由表可知：
(9.3+1.8)/2=5.55
$$D(1,2)=(9.3-5.55{)}^2+(1.8-5.55{)}^2=28.125$$
(9.3 +1.8+1.9)/3=4.333
$$D(1,3)=(9.3-4.333{)}^2+(1.8-4.333{)}^2+(1.9-4.333{)}^2=37.007$$
依次计算可以得到：

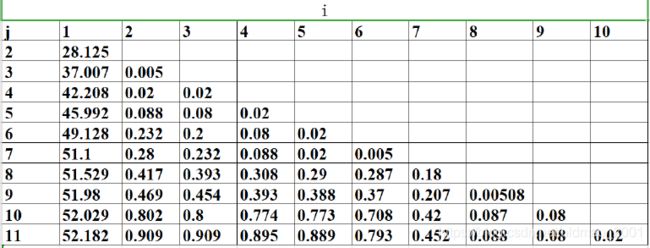
假如我们要计算前面四个样本的损失函数的最小情况：
$$L[P(4,2)]=\underset{2\le j\le 4}{\min }\{D(1,j-1)+D(j-1,4)\}$$
这个时候有三种情况
①1号样本为一类，234号样本为一类：$D(1,1)+D(2,4)=0+0.02$
②12号样本为一类，34号样本为一类：$D(1,2)+D(3,4)=28.125+0.02$
②123号样本为一类，4号样本为一类：$D(1,3)+D(4,4)=37.007+0$
可以看到损失值最小的分法是第一种。
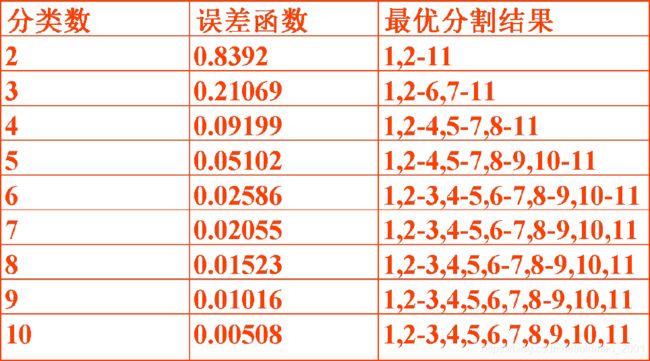
因此可以得到最⼩损失函数L[P(n,k)]表：

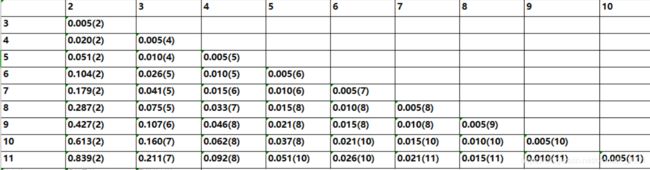
上表中行是分类数k，列号是样本数n
这里样本数n=11，最左下角那个0.839代表将11个样本分为2类，最小的loss是0.839，括号里面的2代表从第2个样本到最后一个样本分为一类
如果将11个样本分为3类，那么最小loss是0.211，括号里面的7代表从第7个样本到最后一个样本分为一类，然后从第2个样本到第6样本分为一类，第1个样本为一类

根据上表可以得到损失函数L[P(n,k)]随分类数k变化趋势图：

分类数越大，损失越小，但是工作量越大，因此要做tradeoff，这里选3或者4做为分类结果。
最后例题有序样本聚类结果：