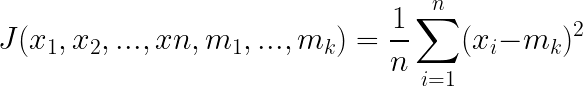机器学习之聚类算法:K均值聚类（一、算法原理）

目录

一、Kmeans

二、Kmeans的流程 

三、距离度量方式 

3.1、闵可夫斯基距离

3.2、马哈拉诺比斯距离

3.3、其他

四、Kmeans聚类实例

五、Kmeans存在的问题

5.1、初始点的选择 

 5.2、K值的选择

5.3、大数据量的聚类

5.4、非球形数据 

六、解决办法

6.1、代价函数 

6.2、肘部法则

6.3、min-batch Kmeans

6.4、DBSCAN

---

一、Kmeans

聚类是针对给定的样本，依据他们特征的相似度或者距离，将其归并到若干个“类”或“簇”的数据分析问题。聚类属于无监督学习算法，它的分类依据是样本的相似度或距离，而类或簇的类别事先并不知道，也就是说样本并没有标签。

常见的聚类算法包括Kmeans、层次聚类和DBSCAN,本篇主要介绍K均值聚类。

Kmeans是基于样本集合划分的聚类算法。Kmeans将样本集合划分为k个子集，构成K个子类，每个子类有一个聚类中心，按照一定的度量规则，将每个样本归为其距离最近的聚类中心所在的类。每个样本距离最近的聚类中心只能有一个，所以每个样本也只有一个分类，所以Kmeans属于硬聚类。

二、Kmeans的流程 

该算法的流程非常简单，就是不断地迭代，向着同一类的所有样本离该类的聚类中心距离之和最小的方向去调整聚类中心的位置和所有样本点的归属，直到找到最佳的K个聚类中心并且所有样本已找到最佳归属。

算法的流程为：

（1）初始化：随机的选择K个样本点作为K个初始的聚类中心。

（2）对样本进行聚类：计算每个样本到每个剧烈中心的距离，将每个样本归类到与其相聚最近发聚类中心所在的类中。

（3）计算新的聚类中心：计算每个类中所有样本的均值作为新的聚类中心。

（4）如果聚类中心不在发生改变或者到达截至条件就停止迭代，否则重复（2）和（3）。

Kmeans的计算复杂度为O(mnk)，m为样本维度，n为样本个数，k为类别数。

三、距离度量方式 

3.1、闵可夫斯基距离

闵可夫斯基距离越大，样本之间的相似度就越小，闵可夫斯基距离越小，样本之间相似度就越大。当其值为0代表两者为同一个样本。x=(x1,x2,...,xn),y=(y1,y2,...yn,)定义两者之间的闵可夫斯基距离d为：

                                                                              

其中p大于等于1，p=1时，称为曼哈顿距离，p=2时称为欧几里得距离，简称欧氏距离，当p为无穷大时称为切比雪夫距离，此时距离为各个坐标数值差的绝对值的最大值 。

如下图，图中绿线代表x1与x2之间的欧氏距离，红线代表两者之间的曼哈顿距离。 

3.2、马哈拉诺比斯距离

 马哈拉诺比斯距离，简称马氏距离，它考虑各个分量之间的相关性并与各个分量的尺度无关。

给定一个样本集合，其协方差矩阵记作S，则样本xi与xj之间的马氏距离为：

                                                   

可以看出，当S为单位矩阵时，即数据样本的各个分量相互独立且各个分量的方差为1是，马氏距离退化为欧氏距离，所以马氏距离是欧氏距离的推广，它弥补了欧氏距离将不同属性平等对待的缺点。

3.3、其他

其他常用的距离度量方式还有像相关系数、夹角余弦等，两者均可以表示样本的相似度。相关系数的绝对值为0到1之间，越接近1相似度就越大，接近1为正相关，接近-1为负相关。夹角余弦越接近1表示越相似，越接近0表示越不相似。 

四、Kmeans聚类实例

给定一个样本集合X={x1=(0,2)、x2=(0,0)、x3=(1,0)、x4=(5,0)、x5=(5,2)}，将其聚为两类。

首先随机取两个点作为聚类中心，这里可以在数据范围内随机生成，也可以直接取两个样本点作为聚类中心。这里我们取m1=x1=(0,2),m2=x2=(0,0)分别作为类G1和G2的聚类中心。那么x1属于G1类，x2属于G2类，接下来计算其他点欧式距离的平方（比较大小用平方即可，不影响结果且易于计算）：

 对于x3:d(x3,m1)=5,d(x3,m2)=1,故x3分到类G2中；

对于x4:d(x4,m1)=29,d(x4,m2)=25,故x4分到类G1中；

对于x5:d(x5,m1)=25,d(x5,m2)=29,故x5分到类G1中；

此时：G1={x1,x5},G2=(x2,x3,x4),重新计算样本中心：m1=((0+5)/2,(2+2)/2)=(2.5,2);m2=((0+1+5)/3,(0+0+0)/3)=(2,0).

重新计算距离后，可得：G1={x1,x5},G2={x2,x3,x4}.由于分类结果并没有改变，所以聚类停止，此时为最终结果。

五、Kmeans存在的问题

5.1、初始点的选择 

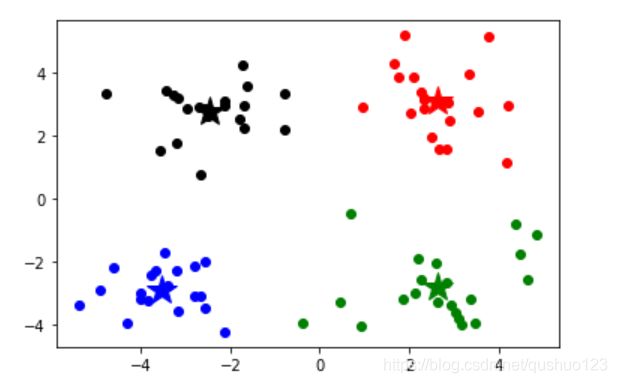
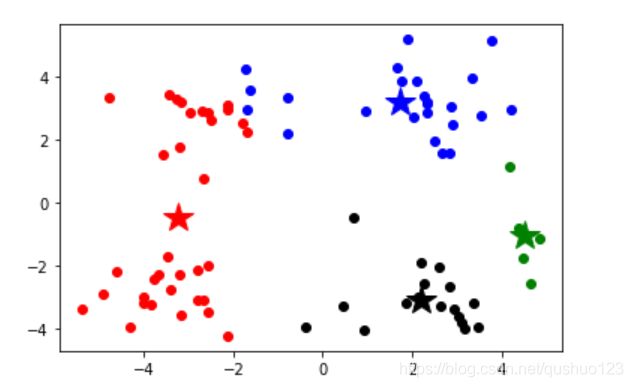
对于不同的初始点，可能会导致不同的聚类结果，当聚类陷入局部最优时，聚类结果就不如人意。如下图所示，左图为比较合理的聚类，右图就是陷入局部最优的聚类。

 5.2、K值的选择

K的选择对最终结果由很大的影响，K值过大会导致聚类过于稀疏，把本应属于一类的数据分成多类，可能会失去数据之间的相关信息；K值过小会导致聚类过于稠密，无法区分不同类别。

5.3、大数据量的聚类

当数据量较大时，由于每次都需要计算距离并比较，复杂度为O(mnk),会导致开销无法接受。

5.4、非球形数据 

Kmeans在处理非球形数据时表现的不尽如人意。如下图的笑脸数据，我们希望按照两个眼睛、嘴巴和轮廓将其分成四类，而按照Kmeans分法，只能得到如下结果。

这里给大家推荐个Kmeans可视化的网站：Kmeans可视化 

六、解决办法

6.1、代价函数 

对于5.1的问题，由于产生的原因是初始化的聚类中心不合理，所以解决办法是多次执行聚类流程，每次迭代完成后计算本次剧烈的代价函数，然后重新初始化并走完整套流程，计算代价函数，多次重复后选择代价函数最小的作为最终结果。 

代价函数的定义为：

其中xi属于的类别为mk。这样多次计算，选择代价函数最小的一个，就可以避免陷入局部最优。

6.2、肘部法则

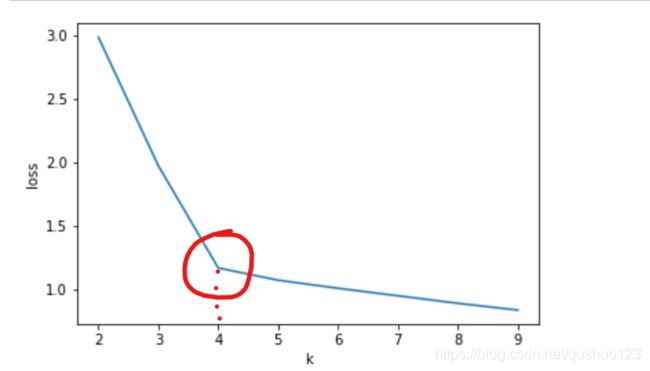
对于5.2的问题，我们可以使K值从小到大递增，分别计算不同K值的损失，画出图像，选择肘部的K值作为最终选择，如图所示，最终选择K=4.

6.3、min-batch Kmeans

 对于5.3的问题，min-batch Kmeans是指选择部分数据进行聚类，根据选出的数据找出剧烈中心，然后将聚类中心作为所有样本数据的聚类中心，这样可以减少计算量，从而处理大规模数据。

研究表明，min-batch Kmeans可以大规模减少计算时间，但结果只是略差于全数据量的Kmeans。

6.4、DBSCAN

对于5.4的问题，采用欧氏距离度量的方式已不再合适，要采用密度度量方式，这样可以把5.4的数据聚类成我们想要的。具体算法我们后续再讨论。