CUDA:矩阵乘法的实现(Share Memory)
本文参加2022CUDA on Platform线上训练营学习笔记
矩阵乘法的GPU端实现
- 一、矩阵乘法(Matrix Multiply)基础
- 二、矩阵乘法的CPU端实现
- 三、矩阵乘法的GPU端实现(Share Memory)
- 四、代码参考
- 五、实践心得
-
- 1、通过__syncthreads()的角色变换
- 2、并行思维中的同步
- 3、提高硬件的使用效率
一、矩阵乘法(Matrix Multiply)基础

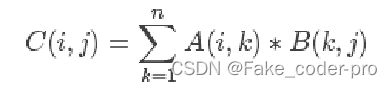
矩阵相乘是线性代数的基础,简单来解释就是A矩阵的行与B矩阵所在列相乘之和的结果,CPU端的代码可以采用模拟思想非常好编写,相信聪明的你一定熟练掌握了矩阵相乘,这里就不做多的介绍了
二、矩阵乘法的CPU端实现
void cpu_matrix_mult(int* h_a, int* h_b, int* h_result, int m, int n, int k) {
for (int i = 0; i < m; ++i)
{
for (int j = 0; j < k; ++j)
{
int tmp = 0.0;
for (int h = 0; h < n; ++h)
{
tmp += h_a[i * n + h] * h_b[h * k + j];
}
h_result[i * k + j] = tmp;
}
}
}
CPU端的代码主要采用了模拟思想,外两层循环,遍历了在结果矩阵中的位置,第三层循环,遍历了A矩阵的行与B矩阵的列,进行相乘求和,可以思考的是如果A矩阵与B矩阵的规模足够大,将是一个巨大的计算任务,在CPU端的串行执行,将面临巨大的压力。因此我们可以集合并行编程思想,使用CUDA代码来实现。话不多说,开始GPU端代码的编写
三、矩阵乘法的GPU端实现(Share Memory)
考虑到矩阵的规模足够大,本篇的代码在实现过程中,直接考虑了GPU Share Memory不足的情况,采用了移动tile的形式来解决这一问题。
在前几篇CUDA学习介绍中,我们已经成功实现出了没有使用Share Memory的版本,代码如下:
__global__ void gpu_matrix_mult(int* d_a, int* d_b, int* d_c, int m, int n, int k) {
int row = threadIdx.y + blockDim.y * blockIdx.y;
int col = threadIdx.x + blockDim.x * blockIdx.x;
if (row < m && col < k) {
for (int i = 0; i < n; i++) {
d_c[row * k + col] += d_a[row * n + i] * d_b[col + i * k];
}
}
}
d_a,d_c,d_b都是存在于全局内存中的数组,该代码在执行的过程中会多次访问Global Memory,由于Global Memory的latency比较高,所以大大降低了代码执行的效率,所以我们引入了Share Memory来进行优化,主要采用了Share Memory的一次写入多次读取来降低执行过程中在数据传输方面的损耗。先使用__share__ 标识符来定义两个存在于共享内存中的数组
__shared__ int smem_m[BLOCK_SIZE][BLOCK_SIZE];
__shared__ int smem_n[BLOCK_SIZE][BLOCK_SIZE];
本篇中采用的是正方形的tile 大小为当前Block的大小。在核函数的代码当中,每个线程将扮演两个角色:1.将Global Memory中的数据赋值到Share Memory中,2.计算当前的矩阵中的值。我们的代码使用了移动tile 的方法拷贝时将一个一个tile边移动边拷贝边计算,具体如下图所示,smem_m将向x轴的正方向移动,smem_n将向y轴正方向移动,步长为当前tile的边长,移动过程中涉及到了一个sub概念,即当前tile移动的步数,tile的总步数为n / BLOCK_SIZE 向下取整即可

for (int stride = 0; stride <= n / BLOCK_SIZE; stride++) {
int idm = stride * BLOCK_SIZE + row * n + threadIdx.x;
if (row < m && BLOCK_SIZE * stride + threadIdx.x < n) {
smem_m[threadIdx.y][threadIdx.x] = a[idm];
}
else {
smem_m[threadIdx.y][threadIdx.x] = 0;
}
int idn = stride * BLOCK_SIZE * k + col + threadIdx.y * k;
if (col < k && BLOCK_SIZE * stride + threadIdx.y < n) {
smem_n[threadIdx.y][threadIdx.x] = b[idn];
}
else {
smem_n[threadIdx.y][threadIdx.x] = 0;
}
__syncthreads();
for (int i = 0; i < BLOCK_SIZE; i++) {
tmp += smem_m[threadIdx.y][i] * smem_n[i][threadIdx.x];
}
__syncthreads();
}
由于当前线程在A中拷贝的位置与在B中拷贝的位置不同,所以要分开计算idm和idn,确保所有线程都参加集体活动完毕,我们采用__syncthreads()函数来同步当前block中的线程,同步完成之后将当前tile涉及到的计算步骤算出结果存在临时的tmp中,在tile执行完所有移动时,将tmp赋值到我们的global Memory中。
if (row < m && col < k)
{
c[row * k + col] = tmp;
}
需要特别注意的是,条件的判断,当前线程各自有着各自的计算任务,也有着当前的集体任务(将数据从Global Memory中拷贝到Share Memory当中),不能因为各自的计算任务的无效而不参加集体任务。
通过上述分析,我们获得了完整的使用了Share Memory优化版本GPU代码
__global__ void gpu_matrix_mult(int* a, int* b, int* c, int m, int n, int k)
{
__shared__ int smem_m[BLOCK_SIZE][BLOCK_SIZE];
__shared__ int smem_n[BLOCK_SIZE][BLOCK_SIZE];
int row = blockDim.y * blockIdx.y + threadIdx.y;
int col = blockDim.x * blockIdx.x + threadIdx.x;
int tmp = 0;
for (int stride = 0; stride <= n / BLOCK_SIZE; stride++) {
int idm = stride * BLOCK_SIZE + row * n + threadIdx.x;
if (row < m && BLOCK_SIZE * stride + threadIdx.x < n) {
smem_m[threadIdx.y][threadIdx.x] = a[idm];
}
else {
smem_m[threadIdx.y][threadIdx.x] = 0;
}
int idn = stride * BLOCK_SIZE * k + col + threadIdx.y * k;
if (col < k && BLOCK_SIZE * stride + threadIdx.y < n) {
smem_n[threadIdx.y][threadIdx.x] = b[idn];
}
else {
smem_n[threadIdx.y][threadIdx.x] = 0;
}
__syncthreads();
for (int i = 0; i < BLOCK_SIZE; i++) {
tmp += smem_m[threadIdx.y][i] * smem_n[i][threadIdx.x];
}
__syncthreads();
}
if (row < m && col < k)
{
c[row * k + col] = tmp;
}
}
四、代码参考
#include 五、实践心得
1、通过__syncthreads()的角色变换
与前几次的代码相比,本篇代码的最大的不同体现在在for函数中有着两个__syncthreads(),通过huan老师的专业又抽象的描述为:每一个线程通过__syncthreads()转换了自己的身份,__syncthreads()之前,每个现在参加集体活动,负责数据的传输,同步之后每个线程负责自己对应的计算。可见__syncthreads()函数对于同一个block中的线程的作用之大。
2、并行思维中的同步
本篇代码体现了并行思维,在share Memory赋值操作中,由于是并行执行的, 所以每个线程执行的速度也有着差异,若不执行同步操作的话,可能会导致线程的计算发生在share Memory的赋值操作之前,导致了错误的计算,线程的同步很好的解决了这一问题,通过同步保证当前block中的线程全部对share Memory赋值完毕,再执行操作,避免了上述问题的出现。可见在并行编程中的同步思维的重要性,该思维的丢失往往在bug的寻找过程中很难弥补,所以在code环节中要谨慎思考,避免在debug环节中的停滞
3、提高硬件的使用效率
本文中的tile的大小的设置为了方便演示和理解,设置成了BLOCK_SIZE*BLOCK_SIZE,实际中应该为其分配更加合理的值,由于每次的移动都是以一个tile大小的share memory来进行赋值的,所以其大小将对性能有着较大的影响。同时为了提高硬件的使用效率,GridDim和BlockDim的设置也需要调优。
