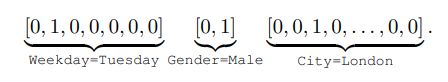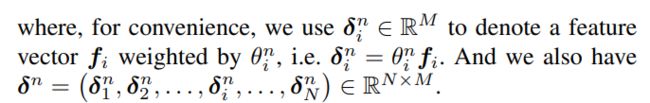PNN论文翻译 - 基于点乘的用户响应神经网络预测（四）

摘要 - 预测用户响应（例如点击次数和转化次数）非常重要，并已在其中使用许多Web应用程序，包括推荐系统，Web搜索和在线广告。这些应用程序中的数据主要是类别特征，包含多个字段;一个典型的表示是将其转换为高维稀疏通过独热编码的二进制特征表示。面对极度稀疏，传统模型可能会限制其从数据中挖掘出的信息，即低阶特征组合。像深度神经网络这样的深层模型，不能直接申请高维输入因为巨大的特征空间。在本文中，我们提出基于点乘的神经网络（PNN），具有嵌入功能层来学习类别数据的分布式表示，一个点乘层来捕捉场间类别之间的交互模式，并进一步完全连接层来探索高阶特征交互。我们的实验结果有两个大型真实世界广告点击数据集演示了PNN在各种方面始终优于最先进的模型指标。

 

I. INTRODUCTION

在信息检索中的许多个性化任务中的作用（IR），学习和预测用户响应现在起着至关重要的作用，例如推荐系统，网络搜索和在线广告。 用户响应预测的目标是估计用户对提供广告表达肯定的概率响应，例如 点击，购买等，在给定的背景下[1]。该预测概率表示用户对该兴趣的兴趣特定项目，如新闻文章，商业项目或广告帖，影响随后的决定制作文件排名[2]和广告投标[3]。

这些IR任务中的数据收集主要采用多字段分类形式，例如，[工作日=星期二，Gender = Male，City = London]，通常通过onehot编码转换为高维稀疏二进制特征[4]。 例如，三个字段向量用独热编码连接为

许多机器学习模型，包括线性逻辑回归[5]，非线性梯度增强决策树[4]和分解机[6]，已被提出工作在这样的高维稀疏二进制特征和产生高质量的用户响应预测。 然而，这些模型高度依赖于特征工程，以捕获高阶潜在模式[7]。

最近，深度神经网络（DNN）[8]已经表明具有很强的分类和回归任务能力，包括计算机视觉[9]，语音识别[10]和自然语言处理[11]。采用DNN很有希望在用户响应预测中，因为DNN可以自动进行学习更具表现力的特征表征并提供更好的表现预测性能。为了改善多字段类别数据交互，[12]提出了嵌入基于分解机器预训练的方法。基于级联嵌入向量，多层构建感知器（MLP）以探索特征交互。但是，嵌入初始化的质量很大由分解机器限制。更重要的是，感知器层的“添加”操作可能没有用探索多个领域中分类数据的交互。以前的工作[1]，[6]已经表明了本地的依赖关系可以通过特征向量“产品”操作而不是“添加”来有效地探索来自不同领域的特征之间的关系操作。

利用神经网络和挖掘潜在的数据模式的学习能力比MLP更有效，在本文中，我们提出了基于点乘的神经网络（PNN）（i）从[12]中使用的没有预训练的嵌入层开始，以及（ii）创建可一个点乘层用于模拟不同特征的嵌入特征向量相互作用关系，以及（iii）进一步提炼高阶特征具有完全连接的MLP的模式。 我们提出两种类型PNN，inner点乘和outer点乘操作图层，有效地模拟交互模式。

我们将在线广告中的CTR估计作为探索PNN模型学习能力的工作实例。两个大型真实世界数据集的广泛实验结果证明了我们的一致优势最先进的用户响应预测模型的模型关于各种指标的[6]，[13]，[12]。

 

II. RELATED WORK

通常制定响应预测问题作为具有预测可能性的二元分类问题或交叉熵作为训练目标[14]。 在ROC曲线的面积（AUC）和相对信息增益（RIG）是响应预测准确性的共同评估指标[15]。 从建模角度看，线性逻辑回归（LR）[5]，[16]和非线性梯度增强决策树（GBDT）[4]和分解机（FM）[6]广泛用于工业应用。 但是，这些模型是限制采用高阶潜在模式或学习质量特征表示。

深度学习能够探索高阶潜在模式以及概括表达数据表示[11]。DNN的输入数据通常是密集的实数向量，而多种类分类特征的解决方案尚未解决还需好好研究。分解机支持的神经网络[12]中提出了（FNN）来学习嵌入向量，通过预先训练的FM来过类别特征。卷积点击[13]中提出了预测模型（CCPM）来预测广告点击卷积神经网络（CNN）。但是，在CCPM只对邻居进行了卷积某个对齐的字段，无法模拟完整非邻居特征之间的相互作用。反复神经利用网络（RNN）将用户查询建模为一系列用户上下文来预测广告点击行为[17]。产品单元神经网络（PUNN）[18]被提出来构建输入的高阶组合。但是，都没有PUNN可以学习本地依赖关系，也不会产生有界的依赖关系输出以适应响应率。

在本文中，我们演示了PNN模型的方式学习本地依赖关系和高阶特征交互

 

III. DEEP LEARNING FOR CTR ESTIMATION

我们将在线广告中的点击率估算[14]作为一个以工作为例来制定我们的模型并探索各种指标的表现。 任务是在给定的背景下建立预测模型来估计用户点击特定的概率广告。

每个数据样本由多个分类字段组成，比如说用户信息（城市，小时等），广告商等数据信息（域名，广告位等）和广告信息（广告创意ID，广告系列ID等）[19]。 所有信息表示为多字段分类特征向量，其中每个字段（例如，城市）是在第I节中讨论过的独热编码。这样一个字段式的单热编码表征导致维数和巨大的稀疏性[12]。 此外，还存在本地依赖关系领域之间的等级结构[1]。

因此，我们正在寻求DNN模型来捕获高阶多分类特征中的潜在模式。 我们来了以“点乘”层的思想来自动探索特征交互。 在FM中，特征交互被定义为内部两个特征向量的乘积[20]。

所提出的深度学习模型被称为基于“点乘”的神经网络（PNN）。 在本节中，我们将介绍PNN模型详细讨论了这个模型的两个变种，即基于内积的神经网络（IPNN），具有内积层和外积神经网络（OPNN）使用外部产品表达。

A. 基于点乘的神经网络PNN模型的体系结构如图1所示。

从自上而下的角度来看，PNN的输出是真实的数y∈（0,1）作为预测的CTR：

是第一个隐藏层的输出。该激活单元（relu），定义为relu（x）= max（0，x），被选为隐藏层输出的激活函数，它具有出色的性能和高效的计算。

第一个隐藏层与“点乘层”直接相连。 它的输入包括线性信号lz和二次方信号lp。 关于lz和lp输入，隐藏层的输入l1可以表达为：

接着，让我们来定义一下 inner product

首先将元素乘法应用于A，B，然后乘法结果总计为标量。 然后，lz和lp分别通过z和p计算：

通过引入“1”恒定信号，产品层可以不仅生成二次信号p，还维持线性信号z，如图1所示。更具体地说，

其中fi就是一个特征域的向量，p(i,j) = g(fi,fj)定义了特征对之间的交叉方式，我们的PNN模型可以通过设计不同的g方式来有不同的实现。在这篇论文中，我们定义了两种方式，IPNN/OPNN，我会在后续对这两个方法进行详细描述，这也是论文中最重要的地方。

fi这个属于特征i的embedding向量，是一个embedding层的输出向量

x是一个包含多个取值的输入特征向量，x[start i:end i]代表了特征i的one-hot表达向量。Wo代表了embedding层的参数，是特征 i 的全连接方式。

最后，使用交叉熵损失作为loss的优化方式，这是一个呗广泛用作目标损失函数来计算概率这种损失的方式

其中y是真实label(1代表点击、0代表不点击)，y^是模型的预测值

 

B. Inner Product-based Neural Netwo

在这一节中，我们会演示IPNN的原理，首先我们定义一个特征交叉的向量表达方式：: g(fi , fj ) =

对于恒定信号“1”，线性信息z被表达为

对于二次信息p，成对内积的方式 g（fi，fj）形成一个平方矩阵 ，回顾一下在公式5中定义的 lp 

表示了向量内积的交换法则，p和Wnp应该是对称的

这种成对连接扩展了神经的网络能力，但也极大地增加了复杂性。 在这案例，l1的公式，如公式1所述。 （3），空间复杂度是 O（D1N（M + N））、时间复杂度是O（N*N（D1 + M）），其中D1和M是网络架构的超参数，M是向量维度，N是输入字段的数量 也就是特征的个数。受FM [20]的启发，我们提出了矩阵的概念分解以减少复杂性

通过第n个单节点上的第一阶分解，我们给lp完整的表达公式

通过减少等式中的lp。 （12），空间复杂l1变为O（D1MN），时间复杂度为O（D1MN）。 通常，l1的复杂性会从二次降低到线性 我们期待是N。这个结构良好的方程可以重复使用某些中间结果。此外，GPU中很容易加速矩阵运算

更一般地，我们在本节末，我们讨论K阶分解。我们应该指出 ，只有强有力的第一阶分解假设。 一般的矩阵分解方法可以派生的

在这种情况下，这种一般分解更多用较弱的假设表达，但也导致模型复杂度上升K倍

 

C. Outer Product-based Neural Netw

取一对向量进行向量内积，然后作为输入和输出标量。 与此不同，向量外积需要一对矢量并产生一个矩阵。 IPNN通过内积方式来定义特征交叉，而在本节中，我们讨论基于“外积”的神经网络（OPNN）

IPNN和OPNN之间的唯一区别是二次项p。 在OPNN中，我们定义了特征交互，因此在P中的每一个元素，都是一个平方矩阵

在计算l1的时候，空间复杂度是  O(D1 * M * M * N * N)，时间复杂度是 O(D1 * M * M * N * N)，回想一下，D1和M是网络架构的超参数，其中M是向量维度，N是输入字段的数量，这个实现在实践中是昂贵的。 为了降低复杂性，我们建议超级的想法

通过逐元素叠加，我们可以通过一大步减少复杂性。 具体来说，我们重新定义p公式

 

D. Discussions

与FNN [12]相比，PNN具有点乘层。 如果除去点乘层的lp部分，PNN与和FNN相同。 对于内积来说，PNN和FM [20]非常相似：如果没有隐藏层和输出层简单地总结一致的重量，PNN和FM是相同的。 受Net2Net [21]的启发，我们可以先训练一部分PNN（例如，FNN或FM部分）作为初始化，和然后开始让反向传播遍及整个网络。产生的PNN至少应该与FNN或FM一样好。

通常，PNN使用点乘层来探索特征交叉方案。 向量点乘可以被视为一系列加法/乘法运算。 内积和外积只是两个实现。 事实上，我们可以定义更普遍或更复杂的点乘层，获得PNN更好地探索特征交互

类似于电子电路，加法就像“或”门一样而乘法就像“AND”门，点乘层是在学习除特征之外的规则。回顾计算机视觉的场景，而图像中的像素是真实的原始特征，Web应用程序中的分类数据具有高水平和丰富意义的人工特征。逻辑是处理概念，域的强大工具和人际关系。 因此我们相信引进产品神经网络中的操作将提高网络的能力用于建模多场分类数据。

 

IV。实验

在本节中，我们将详细介绍我们的实验，包括数据集，数据处理，实验设置，模型比较，以及相应的分析1。 在我们的实验中，PNN模型优于主要的最先进模型在两个真实世界数据集的CTR估算任务中。

在论文的剩余部分是在讨论自己的实验结果，不涉及到算法原理，所以有兴趣的可以自己去了解下

 

论文传送门：https://arxiv.org/pdf/1611.00144.pdf