Pytorch入门 - Day6
文章目录
- 动态计算图和梯度下降入门
-
- 1. Autograd的回溯机制与动态计算图
-
- 1.1 可未分性相关属性
- 1.2 张量计算图定义
- 1.3 计算图的动态性
- 2. 反向传播与梯度计算
-
- 2.1 反向传播的基本过程
- 2.2 反向传播运算的注意事项
- 2.3 阻止计算图追踪
- 2.4 识别叶节点
- 3. 梯度下降思想
-
- 3.1 最小二乘法的局限和优化
- 3.2 梯度下降核心思想
- 3.3 梯度下降的方向和步长
-
- 3.3.1 导数和梯度
- 3.3.2 梯度与方向
- 4. 梯度下降的数学表示
-
- 4.1 梯度下降的代数表示
- 4.2 再次理解步长
- 4.3 梯度下降的矩阵表示
- 5. 手动实现梯度下降
动态计算图和梯度下降入门
1. Autograd的回溯机制与动态计算图
1.1 可未分性相关属性
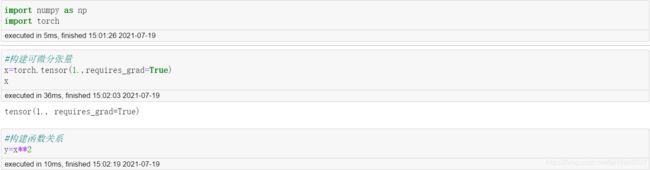
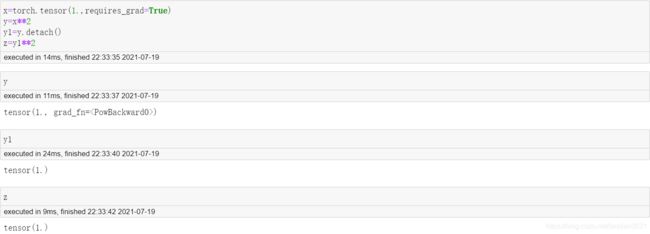
新版Pytorch中的张量不仅仅是一个纯计算的载体, 张量本身也可以进行微分运算.
requires_grad属性: 可微分性
grad_fn属性: 存储Tensor微分函数
1.2 张量计算图定义
借助回溯机制, 我们就能将张量的复杂计算过程抽象为一张图(Graph), 例如此前定义的x,y,z三个张量, 三者的计算关系可由下图进行表示
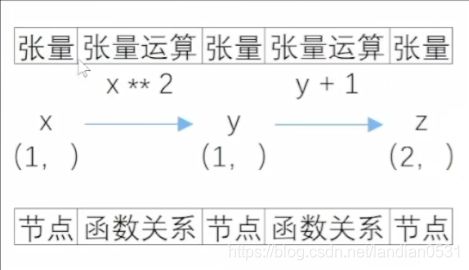
计算图的定义:
用于记录可微分张量计算关系的张量计算图, 图由节点和有向边构成, 其中节点表示张量, 边表示函数计算关系, 方向则表示实际运算方向, 张量计算图本质是有向无环图.
节点类型:
a) 叶节点, 也就是初始输入的可微分张量, 前例中x就是叶节点
b) 输出节点, 也就是最后计算得出的张量, 前例中z 就是输出节点
c) 中间节点, 在一张计算图中, 除了叶节点和输出节点, 其他都是中间节点,前例中y就是中间节点.
1.3 计算图的动态性
根据可微分张量的计算过程自动生成, 并且伴随着新张量或者运算的加入不断更新.
2. 反向传播与梯度计算
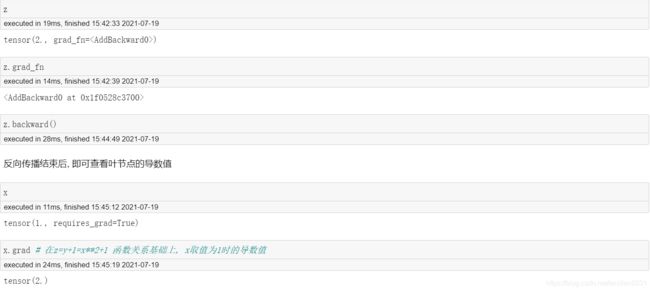
2.1 反向传播的基本过程
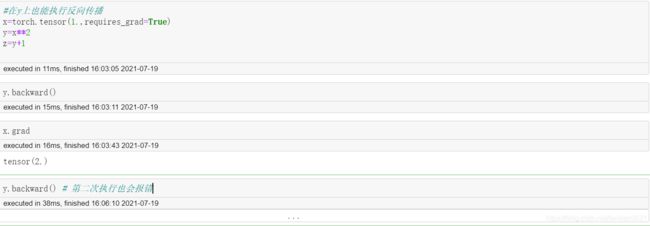
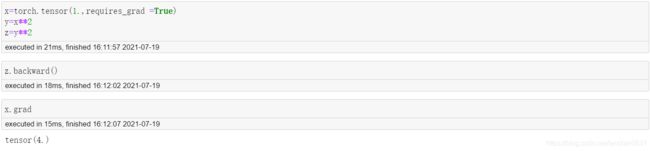
之前使用autograd.grad进行函数某一点的导数值计算, 除了使用函数以外, 还有另外一个放方法, 也能进行导数运算: 反向传播. 此时导数运算结果我们有另外一种解读: 计算梯度结果.
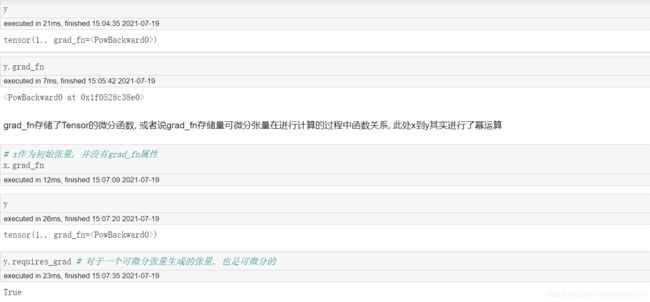
首先, 对于某一个可微分张量的导数值(梯度值), 存储在grad属性中.

最初x.grad属性是空值, 不会返回任何结果. 虽然构建了x, y, z三者之间的函数关系, x也有具体取值, 要计算x点导数, 还需要进行求导运算, 也就是执行所谓的反向传播.
反向传播可以简单理解为, 在此前记录的函数关系基础上, 反向传播函数关系, 进而求得叶节点的导数值, 在必要时求导, 也是节省计算资源和存储空间的必要规定.
反向传播的基本概念和使用方法
a) 本质: 函数关系的反向传播(不是反函数)
b) 执行条件: 拥有函数关系的可微分张量(计算图中除了叶节点的其他节点)
c) 函数作用: 计算叶节点的导数/微分/梯度运算结果
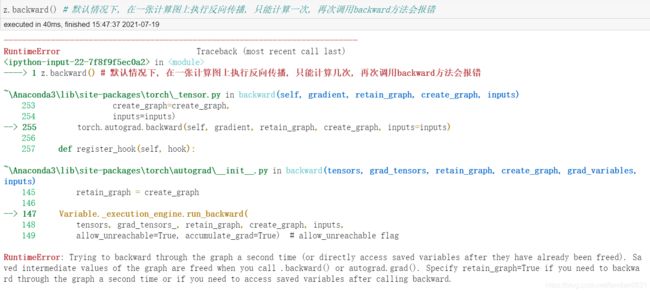
2.2 反向传播运算的注意事项
中间节点反向传播和输出节点反向传播区别:
尽管中间节点也可以进行反向传播, 但很多时候由于存在符合函数关系, 中间节点反向传播的计算结果和输出节点反向传播输出结果并不相同.
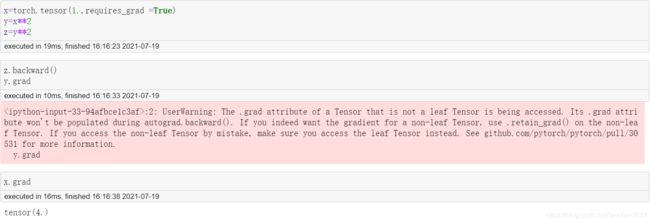
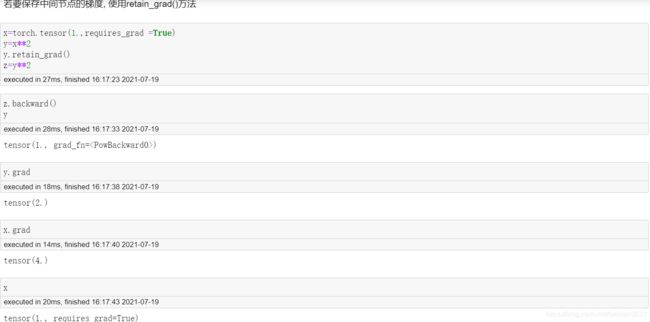
中间节点的梯度保存
默认情况下, 在反向传播过程中, 中间节点并不会保存梯度
2.3 阻止计算图追踪
默认情况下, 只有初始张量是可微分张量, 系统就会自动追踪器相关运算, 并保存在计算图关系中. 我们可以通过grad_fn来查看记录的函数关系, 但特殊情况下, 我们并不希望可微张量从创建到运算结果输出都被记录, 此时可以使用一些方法来阻止部分运算被记录.
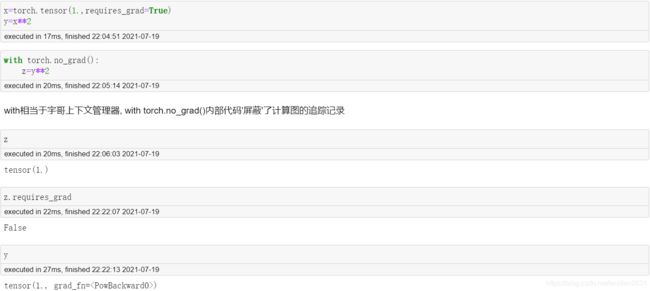
with torch.no_grad(): 阻止计算图记录
例如:
我们希望x,y的函数关系被记录, 而y的后续其他运算不被记录, 可使用with torch.no_grad()来组织部分y的运算不被记录.
.detach()方法: 创建一个不可导的相同张量
在某些情况下, 我们可以创建一个不可导的相同张量参与后续运算, 从而阻断计算图的追踪
2.4 识别叶节点
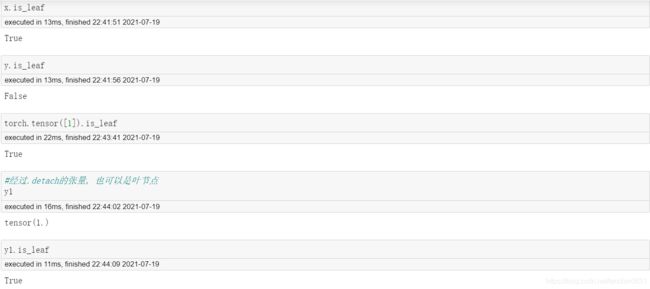
由于叶节点较为特殊, 如果需要识别在一个计算图中某张量是否是叶节点, 可以使用is_leaf属性查看

但is_leaf特殊的地方, 对于任何一个新创建的张量, 无论是否可导,是否加入计算图, 都可以是叶节点, 这些节点距离真正的叶节点, 只差一个requires_grad属性调整.
3. 梯度下降思想
3.1 最小二乘法的局限和优化
最小二乘法的使用条件比较苛刻, 要求特征张量的交叉乘积结果必须是满秩矩阵,才能进行求解.
最小二乘法结果:
w ^ T = ( X T X ) − 1 X T y \hat w^T = (X^T X){^{-1}} X^T y w^T=(XTX)−1XTy
当最小二乘法失效的情况时, 往往代表原目标函数没有最优解或者最优解不唯一. 针对这样情况, 有很多方案, 例如:
在原矩阵方程中加入一个扰动项 λ \lambda λ I I I, 修改后表达式为:
w ^ T = ( X T X + λ I ) − 1 X T y \hat w^T = (X^T X + \lambda I){^{-1}} X^T y w^T=(XTX+λI)−1XTy
其中 λ \lambda λ是扰动项系数, I I I 是单元矩阵.
由矩阵性质可知, 加入单位矩阵后, ( X T X + λ I ) (X^T X + \lambda I) (XTX+λI) 部分一定可逆, 而后即可直接求解 w ^ T ∗ \hat w^{T*} w^T∗, 这也是岭回归的一般做法.
上式修改后求得的结果就不是最全域最小值, 而是一个接近最小值的点.
伴随着深度学习的逐渐深入, 发现最小值并不唯一存在才是目标函数的常态.鉴于此情况, 很多根据等式形变得到的精确的求解的优化方法(如最小二乘)就无法适用, 需要一种更通用, 高效, 快速逼近目标函数优化目标的最优化方法, 在机器学习领域, 最通用的求解目标函数的最优化方法是梯度下降算法.
3.2 梯度下降核心思想
梯度下降算法, 并不是单独的一个算法, 而是某一类依照梯度下降基本理论基础展开的算法簇, 包括梯度下降算法, 随机梯度下降算法, 小批量梯度下降算法等等.
通过数学意义上的迭代运算, 从一个随机点出发, 一步步逼近最优解.
例如, 在此前求解简单线性回归方程的过程中, SSE的三维函数图像如下:
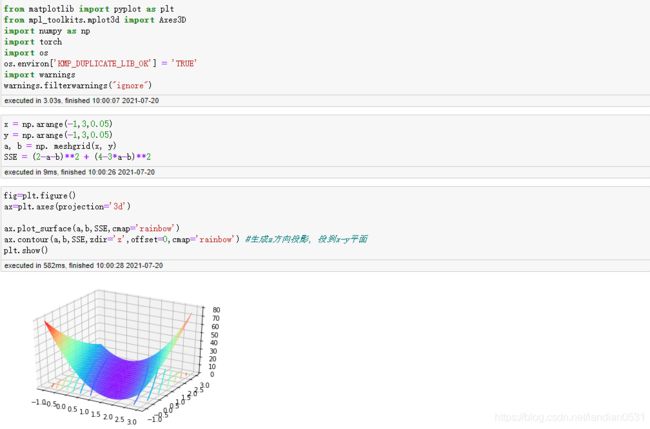
而梯度下降, 作为最优化算法, 核心目标也是找到或者逼近最小值点, 其基本过程:
a) 在目标函数上随机找到一个初始点
b) 通过迭代运算, 一步步逼近最小值点
3.3 梯度下降的方向和步长
关于方向, 梯度下降是采用了一种局部最优推导全域最优的思路, 我们首先是希望能够找到让目标函数变化最快的方向作为移动的方向, 而这个方向就是梯度.
3.3.1 导数和梯度
一般, 函数上某一点的导数值的几何含义就是函数在该点上切线的斜率, 例如y=x**2 , x在1点的导数就是函数在1点的切线的斜率.
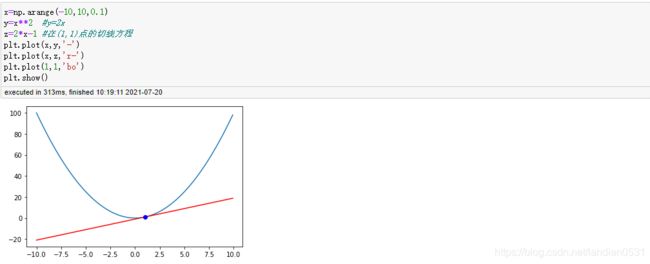
对于上述函数, x取值为1的时候, 导线和切线的斜率为2, 代表含义是给1这个点一个无穷小的增量, 1只能沿着切线方向移动(但仍然在曲线上). 当然, 该点导数值的另一个解释就是该点的梯度, 梯度的值(grad)和导数相同, 而梯度的概念可以视为导数概念的延伸, 只不过梯度更侧重方向的概念, 从梯度的角度解读导数值, 就代表当前这个点可以使得y值增加最快的移动方向
梯度: 梯度本身是一个代表方向的矢量, 代表某一个函数在该点处沿着梯度方向变化时, 变化率最大.
梯度的正方向代表函数值增长最快的方向, 负方向表示函数减少最快的方向.
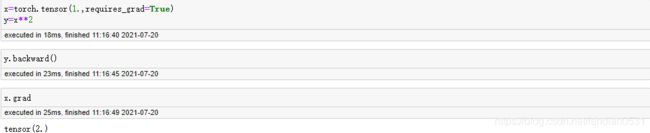
此时由于自变量存在一维空间, 只能沿着x轴变化(左右移动,两个方向)梯度给出的方向只能解读为朝着2, 也就是正方向变化时, y的增加最快.
3.3.2 梯度与方向
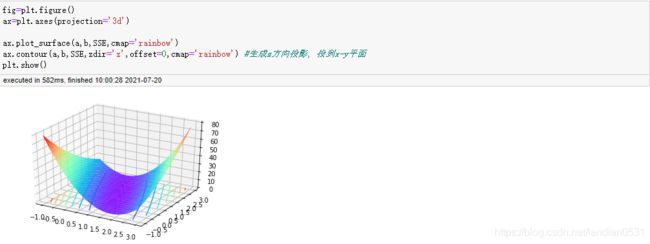
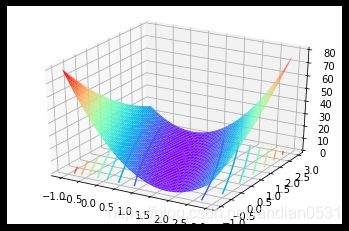
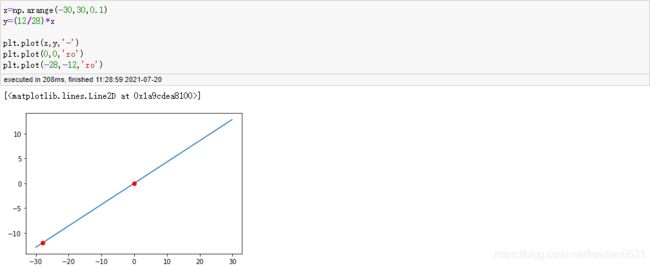
目标函数及其图像如下:
S S E ( a , b ) = ( 2 − a − b ) 2 + ( 4 − 3 a − b ) 2 SSE_{(a,b)} = (2 - a - b)^2 + (4 - 3a - b)^2 SSE(a,b)=(2−a−b)2+(4−3a−b)2
此时a, b实在实数域上取值, 假设二者初始值为0, 也就是初始随机点为原点, 对于(0,0)点, 梯度计算如下:
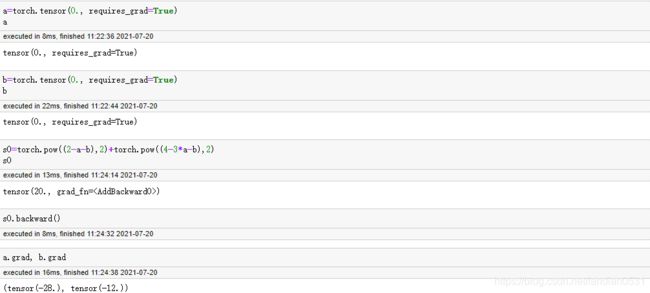
也就是原点和(-28,-12)这个点之间连城直线的方向, 就能够是的SSE变化最快的方向, 并且朝着(-28,-12)方向就是使得SSE增加最快的方向, 反之是令SSE减少最快的方向.
a) 方向没有大小
b) 方向跟随梯度, 随机再发生变化. 需要注意的是, 一旦点发生移动, 梯度就会随之发生变化.
逆梯度值的方向变化时使得sse变小的最快方向, 我们尝试移动’一小步’. 一步移动到(28,12)是没有意义的, 梯度各分量数值的绝对值本身也没有距离这个层面的数学含义. 由于a和b的取值要按照(28,12)等比例变化, 因此我们可以采用如下方法移动:
[ 0 0 ] + 0.01 ∗ [ 28 12 ] = [ 0.28 0.12 ] \begin{bmatrix} {0}\\ {0} \end{bmatrix} +0.01* \begin{bmatrix} {28}\\ {12} \end{bmatrix} =\begin{bmatrix} {0.28}\\ {0.12} \end{bmatrix} [00]+0.01∗[2812]=[0.280.12]
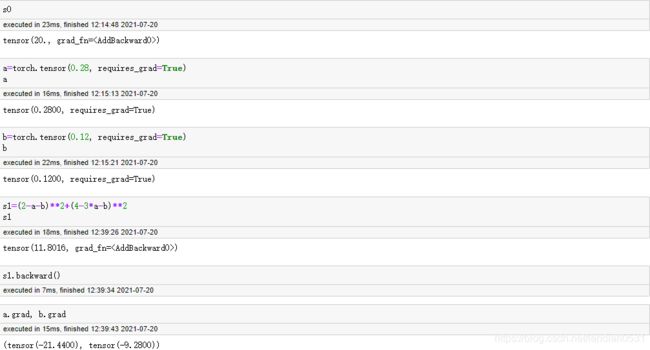
可以看出, 方向已经发生变化. 无论移动多小, 只要移动, 方向就会发生变化. 这里上述0.01称作学习率. 而学习率乘以梯度, 则是原点移动的’长度’.
接下来, 在移动到(0.28,0.12)之后, 还没有取得全域最优解, 因此还需要继续移动, 我们还可以继续按照0.01这个学习率继续移动, 此时,新梯度为(-21.44,-9.28), 则有:
[ 0.28 0.12 ] + 0.01 ∗ [ 21.44 9.28 ] = [ 0.94 0.148 ] \begin{bmatrix} {0.28}\\ {0.12} \end{bmatrix} +0.01* \begin{bmatrix} {21.44}\\ {9.28} \end{bmatrix} =\begin{bmatrix} {0.94}\\ {0.148} \end{bmatrix} [0.280.12]+0.01∗[21.449.28]=[0.940.148]
接下来可以继续计算新的(0.94,0.148)这个点的梯度, 然后继续按照学习率0.01继续移动, 在移动若干次之后,就将得到非常接近于(1,1)的结果.
4. 梯度下降的数学表示
4.1 梯度下降的代数表示
根据上述描述, 可以通过代数运算方式总结梯度下降运算的一般过程
令多元线性回归方程为:
f ( x ) = w 1 x 1 + w 2 x 2 + . . . + w d x d + b f(x) = w_1x_1 + w_2x_2+ ... + w_dx_d +b f(x)=w1x1+w2x2+...+wdxd+b
令
w ^ = ( w 1 , w 2 , . . . , w d , b ) x ^ = ( x 1 , x 2 , . . . , x d , 1 ) \hat w = (w_1, w_2, ... , w_d,b)\\ \hat x = (x_1,x_2, ..., x_d, 1) w^=(w1,w2,...,wd,b)x^=(x1,x2,...,xd,1)
出于加快迭代收敛速度的目标, 我们在定义梯度下降的损失函数 L L L时, 在原SSE基础上进行比例修正, 新的损失函数 L ( w 1 , w 2 , . . . , w d , b ) L(w_1,w_2,...,w_d,b) L(w1,w2,...,wd,b) = 1 2 m S S E \frac1{2m}SSE 2m1SSE, 其中m为样本个数.
损失函数有:
L ( w 1 , w 2 , . . . , w d , b ) = 1 2 m ∑ j = 0 m ( f ( x 1 ( j ) , x 2 ( j ) , . . . , 1 ) − y j ) 2 L(w_1,w_2,...,w_d,b)=\frac1{2m}\sum^m_{j=0}(f(x^{(j)}_1,x^{(j)}_2, ... ,1)-y_j)^2 L(w1,w2,...,wd,b)=2m1j=0∑m(f(x1(j),x2(j),...,1)−yj)2
根据此前描述过程, 在开始梯度下降求解参数之前, 首先需要设置一组参数的初始取值 ( w 1 , w 2 , . . . w d , b ) (w_1, w_2, ... w_d, b) (w1,w2,...wd,b), 以及学习率 α \alpha α, 然后即可执行迭代运算, 其中每一轮迭代过程需要执行以下三步
Step 1. 计算梯度表达式
对于任意一个参数 w w w, 其梯度计算表达式如下:
∂ ∂ w i L ( w 1 , w 2 , . . . w d , b ) \frac{\partial}{\partial w_i}L(w_1,w_2,...w_d,b) ∂wi∂L(w1,w2,...wd,b)
Step 2. 用学习率乘以损失函数梯, 得到迭代移动距离
α ∂ ∂ w i L ( w 1 , w 2 , . . . w d , b ) \alpha \frac{\partial}{\partial w_i}L(w_1,w_2,...w_d,b) α∂wi∂L(w1,w2,...wd,b)
Step 3. 用原参数减Step 2中计算得到的距离, 更新所有的参数 w w w
w i = w i − ∂ ∂ w i L ( w 1 , w 2 , . . . w d , b ) w_i = w_i - \frac{\partial}{\partial w_i}L(w_1,w_2,...w_d,b) wi=wi−∂wi∂L(w1,w2,...wd,b)
更新完所有参数, 即完成一次迭代, 接下来就能以新的一组W_i参与下一轮迭代.
何时停止迭代, 一般来说有两种情况, 其一是设置迭代次数, 到达迭代次数即停止迭代, 其二是设置收敛区间, 即当某两次迭代过程中, 每个 w i w_i wi更新的数值都小于某个预设的值, 即停止迭代.
4.2 再次理解步长
如果损失函数是凸函数, 并且全域最小值存在, 则步长可以表示当前点和最小值点之间距离的比例关系.
a) 步长太短: 会极大影响迭代收敛的时间, 整体计算效率会非常低;
b) 步长太长, 容易跳过最优解, 导致结果震荡.
4.3 梯度下降的矩阵表示
令多元线性回归方程为:
f ( x ) = w 1 x 1 + w 2 x 2 + . . . + w d x d + b f(x) = w_1x_1 + w_2x_2+ ... + w_dx_d +b f(x)=w1x1+w2x2+...+wdxd+b
令
w ^ = ( w 1 , w 2 , . . . , w d , b ) x ^ = ( x 1 , x 2 , . . . , x d , 1 ) \hat w = (w_1, w_2, ... , w_d,b)\\ \hat x = (x_1,x_2, ..., x_d, 1) w^=(w1,w2,...,wd,b)x^=(x1,x2,...,xd,1)
w ^ \hat w w^: 方程系数所组成的向量, 并且我们将自变量系数和截距放到了一个向量中, 此处 w ^ \hat w w^就相当于前例中的a b 组成的向量(a,b)
x ^ \hat x x^: 方程自变量和1共同组成的向量
因此方程可以表示为
f ( x ) = w ^ ∗ x ^ T f(x) = \hat w * \hat x^T f(x)=w^∗x^T
另外, 我们将所有自变量的值放在一个矩阵中, 并且和此前A矩阵类似, 为了捕捉截距, 添加一列全为1的列在矩阵的末尾, 设总共有m组取值, 则
x = [ x 11 x 12 ⋯ x 1 d 1 x 21 x 22 ⋯ x 2 d 1 ⋮ ⋮ ⋮ ⋮ 1 x m 1 x m 2 ⋯ x m d 1 ] x=\begin{bmatrix} {x_{11}}&{x_{12}}&{\cdots}&{x_{1d}}&{1}\\ {x_{21}}&{x_{22}}&{\cdots}&{x_{2d}}&{1}\\ {\vdots}&{\vdots}&{\vdots}&{\vdots}&{1}\\ {x_{m1}}&{x_{m2}}&{\cdots}&{x_{md}}&{1}\\ \end{bmatrix} x=⎣⎢⎢⎢⎡x11x21⋮xm1x12x22⋮xm2⋯⋯⋮⋯x1dx2d⋮xmd1111⎦⎥⎥⎥⎤
对应到前例中的A矩阵, A矩阵就是拥有一个自变量, 两个取值的X矩阵, 令y为自变量的取值, 则有
y = [ y 1 y 2 ⋮ y m ] y=\begin{bmatrix} {y_{1}}\\ {y_{2}}\\ {\vdots}\\ {y_{m}}\\ \end{bmatrix} y=⎣⎢⎢⎢⎡y1y2⋮ym⎦⎥⎥⎥⎤
此时 SSE可表示为:
S S E = ∣ ∣ y − X w ^ T ∣ ∣ 2 2 = ( y − X w ^ T ) T ( y − X w ^ T ) = E ( w ^ ) SSE =||y - X\hat w^T||^2_2 = (y - X\hat w^T)^T (y - X\hat w^T) = E(\hat w) SSE=∣∣y−Xw^T∣∣22=(y−Xw^T)T(y−Xw^T)=E(w^)
梯度下降损失函数为:
L ( w ^ ) = 1 2 m S S E = 1 2 m ( y − X w ^ T ) T ( y − X w ^ T ) L(\hat w) = \frac1{2m}SSE = \frac1{2m} (y - X\hat w^T)^T (y - X\hat w^T) L(w^)=2m1SSE=2m1(y−Xw^T)T(y−Xw^T)
同样, 我们需要设置初始化参数 ( w 1 , w 2 , . . . , w d , b ) (w_1, w_2,..., w_d, b) (w1,w2,...,wd,b) 已经学习效率 α \alpha α, 然后即可开始执行迭代过程, 同样, 每一轮迭代需要有三步计算:
Step 1. 计算梯度表达式
对于参数向量 w ^ \hat w w^, 其梯度计算表达式如下:
∂ ∂ w ^ L ( w ^ ) = 1 m X T ( X w ^ T − Y ) \frac{\partial}{\partial \hat w}L(\hat w) = \frac1mX^T(X\hat w^T - Y) ∂w^∂L(w^)=m1XT(Xw^T−Y)
Step 2. 用学习率乘以损失函数梯度, 得到迭代移动距离
α ∂ ∂ w ^ L ( w ^ ) \alpha \frac{\partial}{\partial \hat w}L(\hat w) α∂w^∂L(w^)
Step 3. 用原参数减Step 2中计算得到的距离, 更新所有的参数 w w w
w ^ = w ^ − α ∂ ∂ w ^ L ( w ^ ) = w ^ − α m X T ( X w ^ T − Y ) \hat w = \hat w - \alpha\frac{\partial}{\partial \hat w}L(\hat w) = \hat w - \frac{\alpha}mX^T(X\hat w^T - Y) w^=w^−α∂w^∂L(w^)=w^−mαXT(Xw^T−Y)
更新完所有参数, 即完成了一轮迭代, 接下来就能以新的 w ^ \hat w w^参与下一轮迭代.
5. 手动实现梯度下降
根据上述矩阵表示的梯度下降公式, 围绕之前简单线性回归的目标函数, 已经Autograd模块中的梯度计算功能, 来进行手动求解梯度下降.
1 ∗ a + b = 2 3 ∗ a + b = 4 1*a+b=2\\ 3*a+b=4 1∗a+b=23∗a+b=4
在转化为矩阵表示的过程中, 我们令
x = [ 1 1 3 1 ] x=\begin{bmatrix} {1}&{1}\\ {3}&{1}\\ \end{bmatrix} x=[1311]
y = [ 2 4 ] y=\begin{bmatrix} {2}\\ {4}\\ \end{bmatrix} y=[24]
w ^ = [ a b ] \hat w = \begin{bmatrix} {a}\\ {b}\\ \end{bmatrix} w^=[ab]
手动尝试实现一轮迭代:
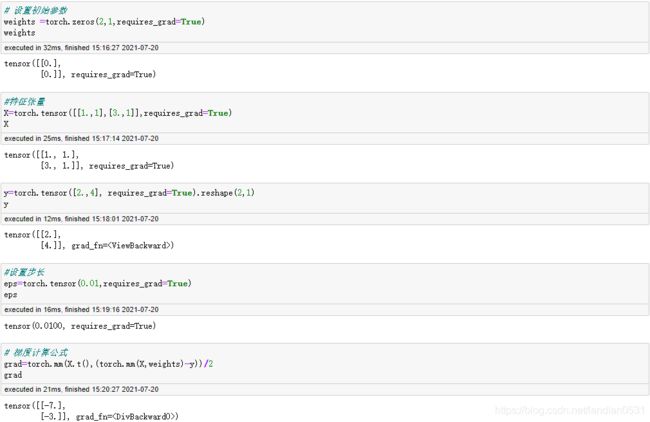
对比代数方程计算结果, 初始梯度为(-28,-12), 此处相差4, 也就是2m, m是样本个数.
迭代3次