视觉SLAM十四讲——第8讲视觉里程计2（光流法和直接法）

参考博客（写的很好）：

SLAM光流法、直接法代码踩坑记录

1.代码运行问题记录

1.1.需要OpenCV4版本

从CMakeLists.txt文件中的设置就可以看到需要使用OpenCV4的版本，因为电脑上的OpenCV是装ROS的时候附带装的OpenCV，应该是OpenCV3.3.1，所以此时需要再装一个OpenCV4，这就涉及到了OpenCV的版本共存。

安装笔记：ubuntu下安装多版本的opencv

1.2.修改代码使用OpenCV4接口

安装好OpenCV4之后，如果直接运行代码，会报错如下：

error: ‘CV_GRAY2BGR’ was not declared in this scope
     cv::cvtColor(img2, img2_single, CV_GRAY2BGR);
                                     ^~~~~~~~~~~

此时需要把CV_GRAY2BGR改为OpenCV4中的接口COLOR_GRAY2BGR。

注意，在CH8里有两个程序，一个是optical_flow.cpp，一个是direct_method.cpp。这两个文件中的程序都用到了cv::cvtColor(img2, img2_single, CV_GRAY2BGR);这个函数，但是他们的编写有一点不同。在optical_flow.cpp中，声明了cv的命名空间，所以修改的时候直接把CV_GRAY2BGR改为OpenCV4中的接口COLOR_GRAY2BGR即可。

但是在direct_method.cpp没有声明cv这个命名空间，而原来的函数是这样的：cv::cvtColor(img2, img2_show, CV_GRAY2BGR);，如果此时还像上一个文件那样更改，那么修改之后编译还是会报和上面同样的错误，实际上原因就在于第二个文件中没有使用cv的命名空间，而CV_GRAY2BGR恰好又是定义在这个命名空间下的，所以会报这样的错误（由此课件原来的代码中的 CV_GRAY2BGR在高博使用的OpenCV的版本下应该是不在cv这个命名空间下也可以找到的）。因此这个文件的正确改法就是在变量前面加上cv的命名空间即可：cv::cvtColor(img2, img2_show, cv::COLOR_GRAY2BGR);。

1.3.Pangolin的fmt依赖问题

这个fmt到底是干什么的不知道，好像是格式化输出需要的？但是Pangolin是依赖于它的。可能是由于我现在安装的Pangolin的版本问题，高博的源码在CH4的文件中出现了这样的语句：

option(USE_UBUNTU_20 "Set to ON if you are using Ubuntu 20.04" OFF)
find_package(Pangolin REQUIRED)
if(USE_UBUNTU_20)
    message("You are using Ubuntu 20.04, fmt::fmt will be linked")
    find_package(fmt REQUIRED)
    set(FMT_LIBRARIES fmt::fmt)
endif()
include_directories(${Pangolin_INCLUDE_DIRS})
add_executable(trajectoryError trajectoryError.cpp)
target_link_libraries(trajectoryError ${Pangolin_LIBRARIES} ${FMT_LIBRARIES})

课件这里说Ubuntu20才需要加fmt的依赖，但是我是Ubuntu18不加这个依赖还是会报错。所以干脆后面使用Pangolin的时候就把fmt的依赖加上。也就是CMakeLists.txt中增加下面几句，这样编译就不会有问题了。

find_package(fmt REQUIRED)
set(FMT_LIBRARIES fmt::fmt)
target_link_libraries(xxx ${Pangolin_LIBRARIES} ${FMT_LIBRARIES})

1.4.其他问题

主要就是遇到了上面几个问题，其他的小问题（比如传入的图片路径不对等可能会导致OpenCV运行出错）在最上面的参考笔记中已经写了。

2.光流法详解

2.1.光流法原理

利用灰度不变假设，直接寻找第一张图片中的某些点在第二章图片中的位置。这样就相当于只需要在第一张图片中计算特征点，而后面的图片不需要计算特征点再匹配，而是直接寻找和第一张图中的特征点相匹配的点。假设第一张图中的特征点的位置是(x, y)，假设这个点对应到第二张图像中的位置为(x+dx, y+dy)，那么光流法就是根据这两个点的灰度相等的假设去求解dx和dy，从而得到第二张图中的特征点位置。

实际中对于一个特征点的计算不是仅仅根据这个点的灰度，而是选择以这个点为中心的一个小窗口，即为pattern，然后算这个pattern内所有点的灰度，认为这个pattern在第二张图的对应位置灰度都是不变的，这样可以提高鲁棒性？

2.2.高斯牛顿优化实现单层光流

如上图所示，为高斯牛顿法计算光流的公式推导。

根据光流法的原理，定义原来图片中特征点的灰度值和估计的第二张图片中对应的点的灰度值的差为残差，其中要估计的变量就是两种图之间的像素运动（dx, dy）。所以根据高斯牛顿法就需要对这个残差求雅克比，对残差求导很简单，因为因变量(dx, dy)都在I2中，所以就是I2对dx和dy求导，这个导数恰好就是第二张图片中估计的点的灰度梯度。图像梯度就是使用中值差分，也就是上面的公式①。

但是还有一个问题：由于优化问题是迭代的，也就是每次根据求出的(dx, dy)更新第二张图中估计的像素点位置，但是很明显这里(dx, dy)每次求得基本上都是一个小数，在下一次迭代的时候坐标就是小数，就要获得小数的坐标的图像灰度值，显然在原图中是没有这个小数坐标的灰度值的，这个时候就需要进行插值。由于图像有x,y两个维度，所以这里使用的是双线性插值。

2.3.双线性插值获得浮点坐标的灰度值（用于迭代）

2.3.1.原理

双线性插值讲解： 一篇文章为你讲透双线性插值

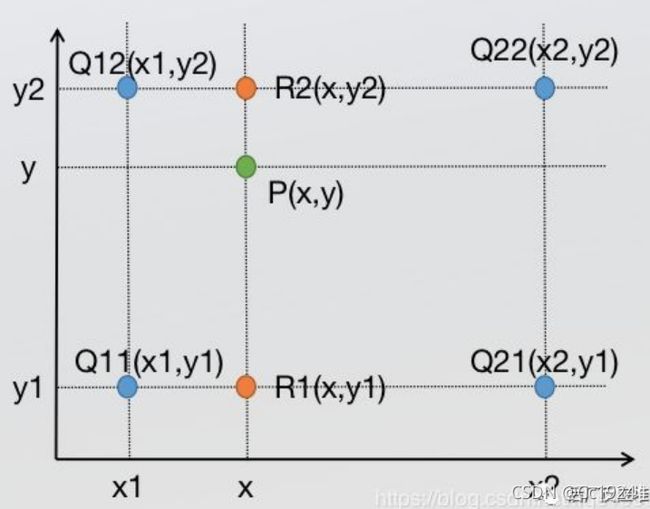
原理很简单，就是先在x方向插值两个点的像素坐标，然后链接这两个点得到一条竖线，再在这条竖线上插值y点的像素坐标。如下图是上面高斯牛顿的博客中写的，写的不太清楚，原理和上面的原理是一样的。

2.3.2.实际操作

实际操作中，为了提高灰度估计值的准确性，肯定是使用离这个浮点坐标最近的两个整数坐标进行插值计算。假设当前要估计的灰度的浮点坐标是（2.x, 5.y），其中x,y是坐标的小数部分，则如下图所示：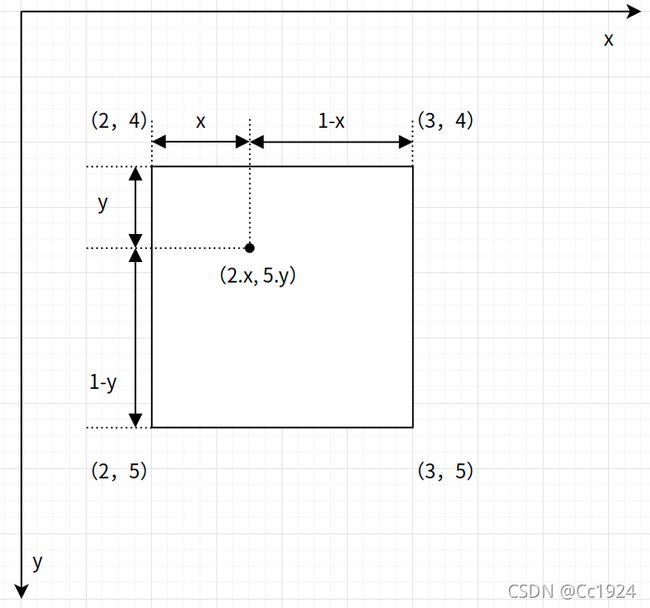

对应的程序如下：

inline float GetPixelValue(const cv::Mat &img, float x, float y) {
    // boundary check
    if (x < 0) x = 0;
    if (y < 0) y = 0;
    if (x >= img.cols) x = img.cols - 1;
    if (y >= img.rows) y = img.rows - 1;
    // img.step是一行像素所占的字节数，这里得到的*data就是指向当前x,y都向下取整的坐标的指针
    uchar *data = &img.data[int(y) * img.step + int(x)];
    float xx = x - floor(x);  // 小数部分x
    float yy = y - floor(y);  // 小数部分y
    return float(
        (1 - xx) * (1 - yy) * data[0] +  // data[0]就是(int x, int y)
        xx * (1 - yy) * data[1] +        // data[1]就是(int x + 1, int y)
        (1 - xx) * yy * data[img.step] + // data[img.step]就是(int x, int y + 1)，注意data便宜img.step就相当于指向下一行相同x位置的像素
        xx * yy * data[img.step + 1]     // data[img.step + 1]就是(int x + 1, int y + 1)
    );
}

2.3.3.程序疑问

• 在高博的程序中，可以看到光流法的实现是对于图片1中的每一个点，在它周围选一个pattern，然后用pattern中的所有点的灰度不变假设，进行迭代10次优化得到dx, dy。也就是对于不同的点，最后迭代得到的dx, dy是不一样的。按理说所有点的(dx, dy)不应该是相同的吗？
• 反向光流法的原理没明白

2.4.多层光流原理

这个比较容易明白，主要是为了解决优化时候的初始值问题。

3.直接法

3.1.理论推导

关于直接法求雅可比，在视觉SLAM十四讲的第二本数上没有细讲，但是在第一版的书中有详细的推导，如下：

3.2.代码实现

由于上面得到了雅克比的解析形式，所以使用高斯牛顿法进行优化的代码流程和上面使用光流法基本相同。

包括使用图像金字塔，这里使用图像金字塔主要是为了减小图像的非凸性的影响，因为这个雅克比和图像的梯度有关，当运动比较距离的时候，由于图像很强的非凸性，很容易让优化到达一个局部最优点而不是全局最优点。但是当使用金字塔之后，图像被缩小，那样即使很大的运动，但是带来视差上的变化也不大，从而能够减小图像的强非凸性带来的影响。

4.CPU的并行实现

在光流法和直接法的程序中，都能看到下面这句：

// 光流法程序中的使用
parallel_for_(Range(0, kp1.size()),
                  std::bind(&OpticalFlowTracker::calculateOpticalFlow, &tracker, placeholders::_1));

// 直接法程序中的使用
cv::parallel_for_(cv::Range(0, px_ref.size()),
                          std::bind(&JacobianAccumulator::accumulate_jacobian, &jaco_accu, std::placeholders::_1));

这个是用来并行计算的，但是不太懂。

在直接法的程序中，Hassin矩阵的存储还使用到了一种数据类型std::mutex，也是和并行计算有关的。

关于使用CPU的并行计算，基本上都是使用CPU厂家的指令集做并行计算的加速，具体也不太懂，详细还需要去学习。