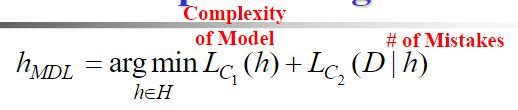机器学习与数据挖掘期末复习

一、引言

1.数据中的知识发现包括哪几个步骤？

数据源—（数据整合）—整理过的数据—（筛选与预处理）—准备好的数据—（选择函数、算法，进行数据挖掘）—模型—（数据评估）—专业知识

2.数据挖掘应用

目标检测、文本分类、语音识别、数据建模、自动驾驶、用户自定义学习、疾病故障自检

二、学习的可行性

1.Hoeffding不等式

2.用Hoeffding不等式说明学习可行性

三、数据和数据预处理

1.有哪四种不同的属性类型？分别可以进行什么操作？

标称属性（nominal）：模、熵、卡方
序数属性（ordinal）：中值、百分比、符号检测
区间属性（interval）：平均值、标准差、
比率属性（ratio）：几何平均数、调和平均数

2.非对称属性？

对属性的关注值不同，比如二元属性，当考虑普通人的患癌情况时，健康时属性为0，患癌时为1，这样大部分情况下该属性都为0，因此我们一般只关注属性为1的情况，所以这个就是非对称的二元属性。

3.数据对象之间相似度、相异度极端

两个对象之间的相似度（similarity）的非正式定义是这两个对象相似程度的数值度量。通常，相似度是非负的，并常常在 0 （不相似）和 1 （完全相似）之间取值。
两个对象之间的相异度（dissimilarity）是这两个对象差异程度的数值度量。通常术语距离（distance）用作相异度的用一次，相异度在 0 和 正无穷大 之间取值。

4.数据预处理的主要任务

数据清理：填写缺失值、光滑噪声数据、识别/删除离群的点
数据集成：将多个数据源上的数据合并
数据变换：数据标准化和数据聚合
数据规约：将巨大的数据规模变小，但分析结果大体相同
数据离散化：增强鲁棒性

5.处理缺失值的方法

1.减少数据集并删除缺失值所在样本
2.找到缺失的值：输入缺失数据的合理预测值、使用一些常量自动替换缺失值、使用其他特征值替换缺失值

决策树学习

1.决策树学习的基本思想

决策树从根节点开始，测试待分类项中相应的特征属性，并按照其值选择输出分支，直到到达叶子节点，将叶子节点存放的类别作为决策结果，以此来实现学习。
其每个非叶节点表示一个特征属性上的测试，每个分支代表这个特征属性在某个值域上的输出，而每个叶节点存放一个类别。
决策树代表了条件对待测试项特征属性的分离。

ppt核心观点：
根节点：每种属性值都会被测试，选择最好的一个（容易分、分的快）去当作根节点的测试方法（就是希望每次选择的属性可以让划分后的分支数据更有区分性，使各个分支的数据分类纯度更高，最好是每个分支的样本数据尽可能属于同一类别。）

为每个属性的可能值创建根节点的后代，并且将训练示例分类到适当的后代节点。

还有个第三点

2.分类错误率，熵，信息增益的概念，如何根据不同度量选择最佳划分

决策树学习的关键在如何选择最优划分属性。一般而言，随着划分过程不断进行，我们希望决策树的分支结点所包含的样本尽可能属于同一类别， 即结点的 “纯度”（purity）越来越高。在分类树中，划分的优劣用不纯度度量（impurity-measure）定量分析。

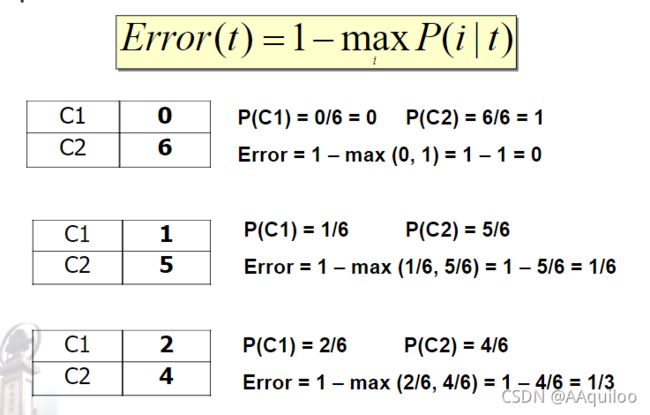
分类错误率

在二分类中，对于任意一个叶子节点，假设其中一个类别A占比（概率）为p，则另外一个类别B的占比（概率）就是1-p。那么，我们可以直观地将分类误差作为损失，即：

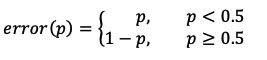
上式表示：当一个叶子类目中的类别A占比较多时（p>0.5），进入该叶子结点的样本就会被判别为类别A，那么剩下的占比为1-p的（类别B）样本则会被分类错误，随之产生的分类误差率就是1-p；反之，当叶子结点中类别A样本较少（p<=0.5）时，该叶子结点就表示类别B，所有进入该节点的类别A样本将会被分类错误，随之产生的分类误差率就是p.

PPT：
分类误差的计算：

熵

信息熵，熵反映了事件的不确定性，对于一般分布事件而言，熵是各种可能性的熵以概率为权重进行加和。

熵的公式为：

属性划分让每个分支纯度更高，所以只需要计算划分前后熵的变化就可以了
1.划分之前计算事件的熵：Ent(X)
2.按照属性 A 划分后再次计算事件的熵：Ent(X|A)
3.则 Ent(X) - Ent(X|A) 就是划分之后熵被消除了多少。
PPT：

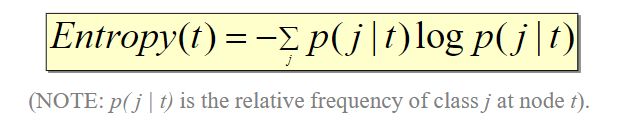
节点不纯度计量方法：

最大：records在所有类中平均分布，代表最少的信息
最小：所有records都是一类，代表大多数信息

熵的计算：

信息增益

因为信息与熵大小相等意义相反，所以消除了多少熵就相当于增加了多少信息，这就是信息增益的由来。
所以信息增益：Gain(X,A) = Ent(X) - Ent(X|A)
其中条件熵的计算：

PPT：

（父节点p被分裂成k划分；ni是划分i的records的数量）
Choose the split that achieves most reduction (maximizes GAIN)
增益率：

3.缺失值对决策树有何影响

①影响不纯度如何计算
②影响如何向子节点分配带有缺失值的实例
③影响带有缺失值的测试实例如何分类

4.给定混淆矩阵，分类效果度量不同指标的含义及计算方法

5.评估分类器性能的留一法和k折交叉验证

留一法：
每次只留下一个样本做测试集，其它样本做训练集，如果有k个样本，则需要训练k次，测试k次。

留一法计算最繁琐，但样本利用率最高。适合于小样本的情况。

k折交叉验证：
1、 将全部训练集 S分成 k个不相交的子集，假设 S中的训练样例个数为 m，那么每一个子 集有 m/k 个训练样例，，相应的子集称作 {s1,s2,…,sk}。
2、每次从分好的子集中里面，拿出一个作为测试集，其它k-1个作为训练集
3、根据训练训练出模型或者假设函数。
4、 把这个模型放到测试集上，得到分类率。
5、计算k次求得的分类率的平均值，作为该模型或者假设函数的真实分类率。

这个方法充分利用了所有样本。但计算比较繁琐，需要训练k次，测试k次。

6.过拟合和欠拟合

过拟合的原因是样本过少，过拟合的结果在决策树上会比所需要的复杂得多
Occam’s Razor：Prefer simpler models
因为训练实例只是所有可能的实例的样本，所以可以在树上添加分支来提高性能，同时降低在本集之外的其他实例上的性能。？？？p70

五、神经网络

1.神经网络如何学习？有何特点？

神经网络通过调整权重来学习，以便能够正确对训练数据进行正确分类，在测试阶段后能够去分类未知的数据。
神经网络需要很长时间去训练。
神经网络对噪声和不完整的数据有很高的忍受度。

神经网络的特点：？？？
神经网络适合的问题域：
输入是高维离散量或实值
输出是离散量或实值
输出是矢量值
目标函数的功能未知
不需要去解释结果（黑盒模型）

2.梯度下降算法

假设空间：
w1、w2平面代表整个假设空间。
对线性单元来说，这个error平面必须是具有单个全局最小值的抛物线
我们想要这个最小值的假设：
由于error平面仅包含单个全局最小值，所以该算法将收敛到具有最小误差的权重向量，无论训练集是否是线性可分离的或给定足够小的η。

梯度下降搜索通过：从任意初始权重向量开始，反复的修改它，在每步在方向上改变权重向量来在error表面熵产生陡峭的下降来确定最小化的权重向量

每个训练样本都以成对的形式
其中x1-xn是输入向量，t 是目标输出值，η 是学习率
以一些小的随机值初始化每个wi
当满足终止条件时，Do：

初始化每个 到0；
对每个训练样本，输入实例到线性单元计算输出o，更新Δwi；
对每个线性单元权重wi进行更新

保证汇聚到最小平方error的假设
最小学习率η
就算训练集有噪声
就算训练集不是线性可分的

3.多层神经网络使用什么算法进行训练？

反向传播算法

六、贝叶斯学习

1.根据贝叶斯理论，如何计算一个假设h成立的后验概率？

2.极大后验概率假设和极大似然假设有何区别？

最大后验概率：
最大后验估计中引入了先验概率
在许多学习场景中，学习器考虑候选假设集合H并在其中寻找给定数据D时，可能性最大的假设h（或者存在多个这样的假设时选择其中之一）。这样的具有最大可能性的假设h被称为极大后验(maximum a posteriori, MAP)假设。

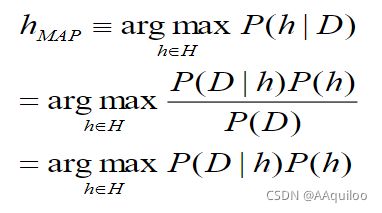
在最后一步，去掉了P(D)，因为它不依赖于h。

极大似然估计：
极大似然估计的核心思想是：认为当前发生的事件是概率最大的事件。因此就可以给定的数据集，使得该数据集发生的概率最大来求得模型中的参数。
极大似然估计只关注当前的样本，也就是只关注当前发生的事情，不考虑事情的先验情况。

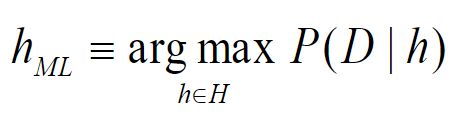
3.最小描述长度的基本思想

最小描述长度准则的信息论解释

极大后验假设所满足的等式，可以等价地表示为使以2为底的对数的负值最小化：

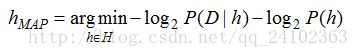
上述等式与我们熟悉的极大后验假设公式完全等价。由此也不难看出：

1. 公式中第一项对应的是——在给定假设 h 时，训练数据 D 的描述长度。也即是发送者和接收者都知道假设 h 时描述数据 D 的最优编码。

2. 公式中第二项对应的是——在假设空间 H 的最优编码下 h 的描述长度。

至此，可以看出：最小描述长度准则默认选用使这两个描述长度的和最小化的假设 h。

对最小描述长度的思考

从信息论的角度看最小描述长度公式，可以把整个学习过程(以分类为例)理解为以下过程：

发送者需要将训练数据 D (包含特征和分类结果)、拟合这些数据的假设 h 以编码的方式传送给接收者。在此处明确一下发送者究竟需要传送哪些必须的信息呢？

训练数据——为了尽量降低编码长度，我们假设发送者和接收者都知道每一个训练数据的特征信息，所以特征信息就不用编码传送。而每一个训练数据的分类结果必须传送吗？答案是N0，因为我们还要讲假设 h 编码传送。如果训练数据的分类结果label 和通过假设 h 预测出的结果一致，那么我们就不需要传送这个数据的标签信息。只有当训练数据预测出错时，才需要将正确的标签信息传送。

假设——假设 h 必须编码传送。并且 h 越复杂， 编码长度越大。如若不明白，可以假设学习器是决策树，对树的编码方法随着决策树节点和边的增长而增加。

其中对训练数据的编码和对假设的编码分别记为 C1 和 C2。

至此可以看出，当 C1 和 C2 分别选取MDL准则中对应的最佳编码方式时训练数据和假设的编码长度之和最小。所选的假设 h 也就是 极大后验假设。

注：从上面的分析可以看出，MDL准则，实际上是假设复杂性（模型复杂度）和假设产生错误的数量之间对的一个折中。MDL 倾向于选择一个产生少量错误而且较短的假设，而不是能完美分类你和训练数据的较长的假设。

4.贝叶斯最优分类器的基本思想

新实例的最可能分类是通过组合所有假设的预测获得的，并按其后验概率加权

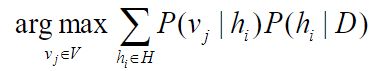
其中 V 是分类可以采用的所有值的集合，vj是这种分类的一种可能

5.朴素贝叶斯分类算法

6.贝叶斯信念网络的预测和诊断

7.偏差方差分析