【深度学习笔记】5.卷积神经网络
CNN
CNN(Convolutional Neural Networks,CNN)中文名叫卷积神经网络。
通常情况下,我们使用全连接神经网络的时候,权重矩阵的参数非常多。其使得整个网络收敛非常缓慢。但在自然图像处理中都具有局部不变性的特征,即尺度缩放、平移、旋转等操作不影响其语义信息,但是全连接前馈网络很难提取这些局部不变特征。所以就引入的CNN。
CNN也是前馈神经网络,其最大的区别是受生物学上感受野的启发,引入了卷积核的概念。
卷积
卷积是一种计算方式,其连续卷积和离散卷积可以表达为如下形式:
{ ( f ∗ g ) ( n ) = ∫ − ∞ ∞ f ( τ ) g ( n − τ ) d τ n = τ + ( n − τ ) ( f ∗ g ) ( n ) = ∑ τ = − ∞ ∞ f ( τ ) g ( n − τ ) \begin{cases} (f*g)(n)=\int_{-\infty}^{\infty}f(\tau)g(n-\tau)d\tau \\ n=\tau+(n-\tau) (f*g)(n)=\sum^{\infty}_{\tau=-\infty}f(\tau)g(n-\tau) \end{cases} {(f∗g)(n)=∫−∞∞f(τ)g(n−τ)dτn=τ+(n−τ)(f∗g)(n)=∑τ=−∞∞f(τ)g(n−τ)
卷积有很多应用,经常用于处理一个输入,通过系统产生一个适应需求的输出。是用于计算信号的延迟累计的一种手段
- 统计学中加权平均法
- 概率论中两个独立变量之和概率密度的计算
- 信号处理中的线性系统
- 物理学的线性系统
- 图像处理中的应用(卷积神经网络)
例如,假设一个信号发生器每个时刻t产生一个信号x,其信息的衰减率为w。即在k-1个时间步长后,信息为原来的w倍。假设w_1=1,w_2=1/2,w_3=1/4,则时刻t收到的信号y_t为当前hi为当前时刻产生的信息和以前时刻延迟信息的叠加,即:
y = 1 ∗ x t + 1 / 2 ∗ x t − 1 + 1 / 4 ∗ x t − 2 = ω 1 ∗ x t + ω 2 ∗ x t − 1 + ω 3 ∗ x t − 2 = ∑ k = 1 3 ω k ∗ x t − k + 1 y=1*x_t+1/2*x_{t-1}+1/4*x_{t-2} \\ =\omega_1*x_t+\omega_2*x_{t-1}+\omega_3*x_{t-2} \\ =\sum^{3}_{k=1} \omega_k*x_{t-k+1} y=1∗xt+1/2∗xt−1+1/4∗xt−2=ω1∗xt+ω2∗xt−1+ω3∗xt−2=k=1∑3ωk∗xt−k+1
其中w就是滤波器,也就是常说的卷积核(Convolution Kernel)
给定一个输入信号x和滤波器w,卷积输出为:
y y = ∑ k = 1 K ω k x t − k + 1 y_y=\sum^{K}_{k=1}\omega_kx_{t-k+1} yy=k=1∑Kωkxt−k+1
而不同的滤波器提取出来的序列也有不同:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-YPAww0VG-1638018363661)(https://datawhalechina.github.io/unusual-deep-learning/PIC/5/3.png)]
步长与零
填充
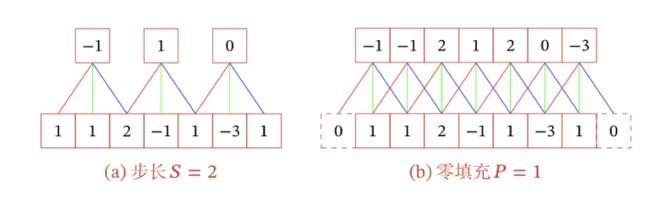
下面引入滤波器的滑动步长S和零填充P:
卷积的结果按输出长度不同可分三类:
- 窄卷积:步长T=1,两端不补零P=0,卷积后输出长度是M-K+1
- 宽卷积:步长T=1,两端补零P=K-1,卷积后的长度是M+K-1
- 等宽卷积:步长T=1,两端补零P=(K-1)/2,卷积后输出长度M
在早期的文献中,卷积一般默认为窄卷积。而目前的文献中,卷积一般默认为等宽卷积。
卷积与图像
上面提到,卷积在图像处理中发挥着重要的左右。而图像一般是二维矩阵的形式输入神经网络中,因此我们需要使用二维卷积。
下面给出定义:一个输入信息X和滤波器W的二维卷积为Y=W*X,既
y i j = ∑ u = 1 U ∑ v = 1 V ω u v x i − u + 1 , j − v + 1 y_{ij}=\sum^{U}_{u=1}\sum_{v=1}V\omega_{uv}x_{i-u+1,j-v+1} yij=u=1∑Uv=1∑Vωuvxi−u+1,j−v+1
实际如下图:
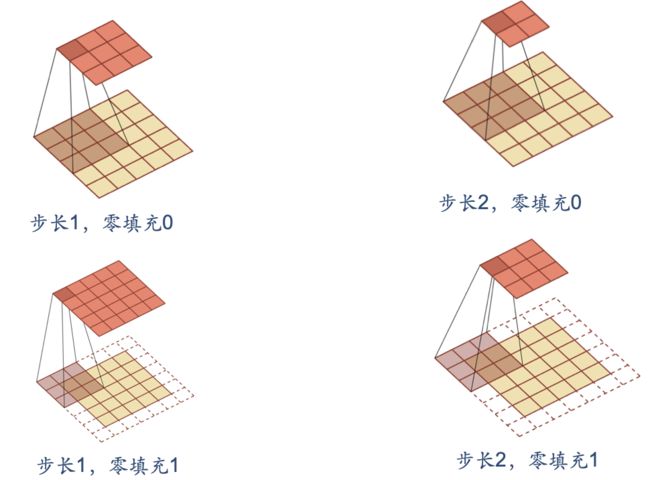
下图直接表示卷积层的映射关系
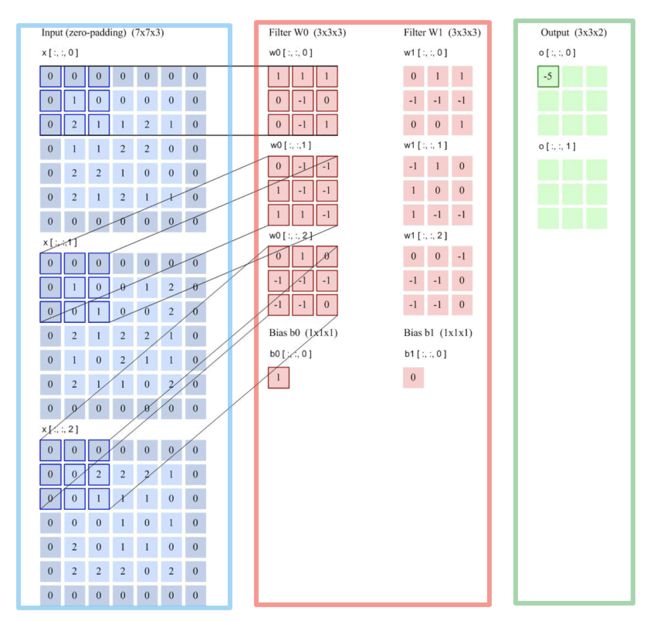
多个卷积核的情况:下图是表示步长2、filter 3*3 、filter个数6、零填充 1的情形。
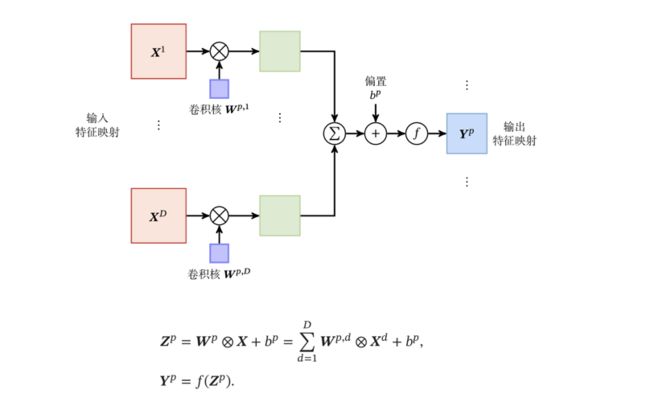
几乎很多实际应用都可以对应到这个问题上,都是在做这样一件事
1)输入对应着rgb图片
2)一旦输入的特征图个数是多个,这个时候每一组filter就应该是多个,而这里有两组filter
3)输入是三个特征图,输出为两个特征图,那么我们同样看看每个特征图怎么计算的。
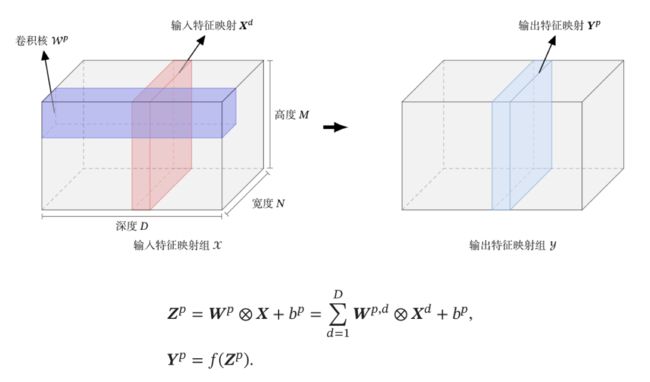
典型的卷积层为3维结构
其他卷积
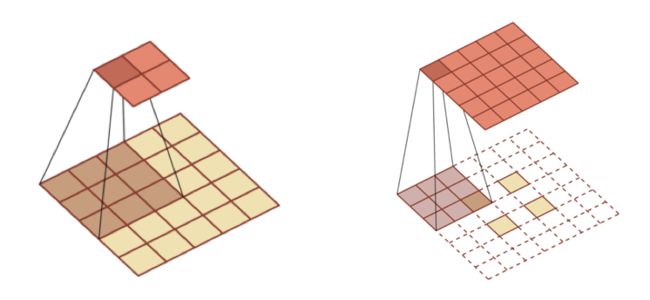
转置卷积/微步卷积
低维特征映射到高维特征
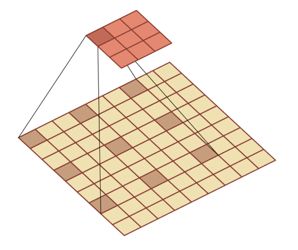
空洞卷积
为了增加输出单元的感受野,通过给卷积核插入“空洞”来变相地增加其大小。
卷积神经网络基本原理
一般的卷积神经网络基本结构包括:输入层、卷积层、激活函数、池化层、全连接层、输出层。当然,在某些特殊业务场景下,可能会基于简单的卷积网络结果添加其他的类似预训练模型、机器学习模型等操作。
下面将从卷积层开始介绍每一层的细节。
卷积层
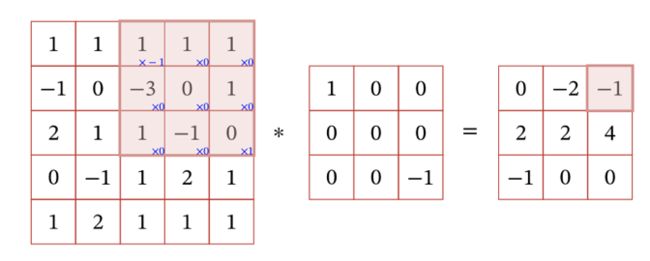
二维卷积运算:给定二维的图片作为输入,卷积核为K,那么卷积的公式可以表示为:
S ( i , j ) = ( I ∗ K ) ( i , j ) = ∑ m ∑ n I ( i − m , j − n ) K ( m , n ) S(i,j)=(I * K)(i,j)=\sum_m\sum_nI(i-m,j-n)K(m,n) S(i,j)=(I∗K)(i,j)=m∑n∑I(i−m,j−n)K(m,n)
绝技和需要进行上下翻转和左右翻转,所以
S ( i , j ) = ( [ I ( i − 2 , j − 2 ) I ( i − 2 , j − 1 ) I ( i − 2 , j ) I ( i − 1 , j − 2 ) I ( i − 1 , j − 1 ) I ( i − 1 , j ) I ( i , j − 2 ) I ( i , j − 1 ) I ( i , j ) ] ∗ [ K ( 2 , 2 ) K ( 2 , 1 ) K ( 2 , 0 ) K ( 1 , 2 ) K ( 1 , 1 ) K ( 1 , 0 ) K ( 0 , 2 ) K ( 0 , 1 ) K ( 0 , 0 ) ] ) S(i,j)=(\left[ \begin{matrix} I(i-2,j-2) & I(i-2,j-1) & I(i-2,j)\\ I(i-1,j-2) & I(i-1,j-1) & I(i-1,j) \\ I(i,j-2) & I(i,j-1) & I(i,j)\end{matrix} \right]*\left[ \begin{matrix} K(2,2) & K(2,1) & K(2,0)\\ K(1,2) & K(1,1) & K(1,0) \\ K(0,2) & K(0,1) & K(0,0)\end{matrix} \right]) S(i,j)=(⎣⎡I(i−2,j−2)I(i−1,j−2)I(i,j−2)I(i−2,j−1)I(i−1,j−1)I(i,j−1)I(i−2,j)I(i−1,j)I(i,j)⎦⎤∗⎣⎡K(2,2)K(1,2)K(0,2)K(2,1)K(1,1)K(0,1)K(2,0)K(1,0)K(0,0)⎦⎤)
卷积实际上就是互相关,其实更直接一点就是输入数据与卷积核对应“坐标”的每一格数据相乘的累加。
累加完毕之后,卷积核会根据我们设定的步长等因素平移,然后继续相乘累加。就犹如下图一样:
![]()
卷积的步长(stride):卷积核移动的步长,决定着卷积核计算完一个单位以后,移动的“距离“
![]()
卷积的模式:Full、Same、Valid
- Full:当卷积核与图片像素开始相交时做卷积
- Same:当卷积核中心(K)与图片像素相交时开始做卷积
- Valid:当卷积核完全与与图片像素相交时开始做卷积
![]()
数据填充:如果我们有一个 × 的图像,使用× 的卷积核进行卷积操作,在进行卷积操作之前我们在图像周围填充 层数据,输出的维度:
![]()
感受野:卷积神经网络每一层输出的特征图(featuremap)上的像素点在输入图片上映射的区域大小,即特征图上的一个点对应输入图上的区域。
![]()
要计算感受野大小,可以采用从后往前逐层计算法:
- 第i层感受野到校和第i-1层的卷积核大小和步长相关,同时也与第i-1层感受野相关
- 假设最后一层(卷积层或池化层)输出特征图感受野的大小(相对于其直接输入而言)等于卷积核的大小
![]()
卷积层的深度(卷积核个数):一个卷积层通常包含多个尺寸一致的卷积核
![]()
激活函数
激活函数是用来加入非线性因素,提高网络表达能力,卷积神经网络中最常用的是ReLU,Sigmoid使用较少。这点在前馈神经网络章节中也有相关提及。
![]()
ReLU函数
优点
- 计算速度快,ReLU函数只有线性关系,比Sigmoid和Tanh要快很多
- 输入为正数的时候,不存在梯度消失问题
缺点
- 强制性把负值置为0,可能丢掉一些特征
- 当输入为负数时,权重无法更新,导致“神经元死亡”(学习率不 要太大)
Parametric ReLU
$$
f(x)=\left{
\begin{aligned}
\alpha x,x<0 \
x,x>0
\end{aligned}
\right.
$$
- 当 =0.01 时,称作Leaky ReLU
- 当 从高斯分布中随机产生时,称为Randomized ReLU(RReLU)
优点
- 比sigmoid/tanh收敛快
- 解决了ReLU的“神经元死亡”问题
缺点
- 需要再学习一个参数,工作量变大
ELU函数
$$
f(x)=\left{
\begin{aligned}
\alpha (e^x-1),x<0 \
x,x\geq0
\end{aligned}
\right.
$$
优点
- 处理含有噪声的数据有优势
- 更容易收敛
缺点
- 计算量较大,收敛速度较慢
总结
激活函数汇总
- CNN在卷积层尽量不要使用Sigmoid和Tanh,将导致梯度消失。
- 首先选用ReLU,使用较小的学习率,以免造成神经元死亡的情况。
- 如果ReLU失效,考虑使用Leaky ReLU、PReLU、ELU或者Maxout,此时一般情况都可以解决
特征图
- 浅层卷积层:提取的是图像基本特征,如边缘、方向和纹理等特征
- 深层卷积层:提取的是图像高阶特征,出现了高层语义模式,如“车轮”、“人脸”等特征
池化层
所谓的池化就是使用某个位置相邻输出的总体统计特征作为该位置 的输出。通俗的讲就是将矩阵中某几个格的数据压缩成1个格。
通常池化会使用最大池化与均值池化。而池化层是不需要训练学习参数读,它只需要指定池化类型、核大小、步幅即可。
假设现有一个3x3的矩阵,核大小为2x2,步幅为1。
![]()
池化的作用
- 减少网络中的参数计算量,从而遏制过拟合
- 增强网络对输入图像中的小变形、扭曲、平移的鲁棒性(输入里的微 小扭曲不会改变池化输出——因为我们在局部邻域已经取了最大值/ 平均值)
- 帮助我们获得不因尺寸而改变的等效图片表征。这非常有用,因为这样我们就可以探测到图片里的物体,不管它在哪个位置
全连接层
- 对卷积层和池化层输出的特征图(二维)进行降维
- 将学到的特征表示映射到样本标记空间的作用
输出层
输出层其实就是全连接成后的一个函数处理。
对于分类问题,输出层有:
y i = e z i ∑ i = 1 n e z i y_i=\frac{e^{z_i}}{\sum^{n}_{i=1}e^{z_i}} yi=∑i=1neziezi
对于回归问题,输出层有:
y i = ∑ m = 1 M ω i m x m y_i=\sum^{M}_{m=1}\omega_{im}x_m yi=m=1∑Mωimxm
卷积神经网络的训练
卷积神经网络大致的训练步骤如下:
- 用随机数初始化所有的卷积核和参数/权重
- 将训练图片作为输入,执行前向步骤(卷积, ReLU,池化以及全连接层的前向传播)并计算每个类别的对应输出概率。
- 计算输出层的总误差
- 反向传播算法计算误差相对于所有权重的梯度,并用梯度下降法更新所有的卷积核和参数/权重的值,以使输出误差最小化
需要注意的是,卷积核个数,核尺寸等参数就如同网络架构一样,在第一步构造完成以后就不会再发生改变。训练中改变的只有卷积核矩阵与神经元的权重。
![]()
和多层神经网络一样,卷积神经网络中的参数训练也是使用误差反向传播算法,关于池化层的训练,需要再提一下,是将池化层改为多层神经网络的形式。
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-XQMDdetf-1638018363673)(https://datawhalechina.github.io/unusual-deep-learning/PIC/5/5.16.png)]
将卷积层也改为多层神经网络的形式
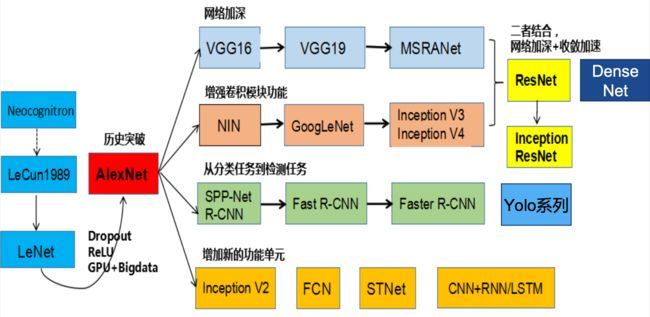
经典卷积神经网络
LeNet-5
LeNet-5由LeCun等人提出于1998年提出,主要进行手写数字识别和英文字母识别。经典的卷积神经网络,LeNet虽小,各模块齐全,是学习 CNN的基础。
参考:http://yann.lecun.com/exdb/lenet/
网络结构
图中输入层是32*32的图片,也就相当于1024哥神经元
C1层(卷积层):选择6个 5∗5 的卷积核,得到6个大小为32-5+1=28的特征图,也就是神经元的个数为6∗28∗28=4704
S2层(下采样层):每个下抽样节点的4个输入节点求和后取平均(平均池化),均值 乘上一个权重参数加上一个偏置参数作为激活函数的输入,激活函数的输出即是下一层节点的值。池化核大小选择 2∗2,得到6个4∗14 大小特征图
C3层(卷积层):用 5∗5的卷积核对S2层输出的特征图进行卷积后,得到6张10∗10 新图片,然后将这6张图片相加在一起,然后加一个偏置项b,然后用 激活函数进行映射,就可以得到1张10∗10 的特征图。我们希望得到 16 张 10*1010∗10 的 特 征 图 , 因 此 我 们 就 需 要 参 数 个 数 为16∗(6∗(5∗5))=16∗6∗(5∗5) 个参数
S4层(下采样层):对C3的16张 10∗10 特征图进行最大池化,池化核大小为2∗2,得到16张大小为 5∗5 的特征图。神经元个数已经减少为:16∗5∗5=400
C5层(卷积层):用 5∗5 的卷积核进行卷积,然后我们希望得到120个特征图,特征图 大小为5-5+1=1。神经元个数为120(这里实际上是全连接,但是原文还是称之为了卷积层)
F6层(全连接层):有84个节点,该层的训练参数和连接数都(120+1)∗84=10164
Output层:共有10个节点,分别代表数字0到9,如果节点i的输出值为0,则网络识别的结果是数字i。采用的是径向基函数(RBF)的网络连接方式:
y i = ∑ j ( x − j − ω i j ) 2 y_i=\sum_j(x-j-\omega_{ij})^2 yi=j∑(x−j−ωij)2
总结:卷积核大小、卷积核个数(特征图需要多少个)、池化核大小(采样率多少)这些参数都是变化的,这就是所谓的CNN调参,需要学会根据需要进行不同的选择。
AlexNet
AlexNet由Hinton的学生Alex Krizhevsky于2012年提出,获得ImageNet LSVRC-2012(物体识别挑战赛)的冠军,1000个类别120万幅高清图像(Error: 26.2%(2011) →15.3%(2012)),通过AlexNet确定了CNN在计算机视觉领域的王者地位。
AlexNet的特点如下:
- 首次成功应用ReLU作为CNN的激活函数
- 使用Dropout丢弃部分神元,避免了过拟合
- 使用重叠MaxPooling(让池化层的步长小于池化核的大小), 一定程度上提升了特征的丰富性
- 使用CUDA加速训练过程
- 进行数据增强,原始图像大小为256×256的原始图像中重 复截取224×224大小的区域,大幅增加了数据量,大大减 轻了过拟合,提升了模型的泛化能力
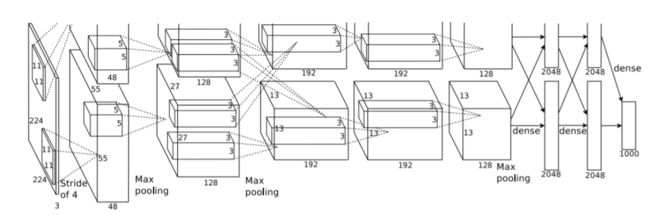
网络结构
AlexNet可分为8层(池化层未单独算作一层),包括5个卷 积层以及3个全连接层
输入层:AlexNet首先使用大小为224×224×3图像作为输入(后改为227×227×3)
第一层(卷积层):包含96个大小为11×11的卷积核,卷积步长为4,因此第一层输出大小为55×55×96;然后构建一个核大小为3×3、步长为2的最大池化层进行数据降采样,进而输出大小为27×27×96
第二层(卷积层):包含256个大小为5×5卷积核,卷积步长为1,同时利用padding保证 输出尺寸不变,因此该层输出大小为27×27×256;然后再次通过 核大小为3×3、步长为2的最大池化层进行数据降采样,进而输出大小为13×13×256
第三层与第四层(卷积层):均为卷积核大小为3×3、步长为1的same卷积,共包含384个卷积核,因此两层的输出大小为13×13×384
第五层(卷积层):同样为卷积核大小为3×3、步长为1的same卷积,但包含256个卷积 核,进而输出大小为13×13×256;在数据进入全连接层之前再次 通过一个核大小为3×3、步长为2的最大池化层进行数据降采样, 数据大小降为6×6×256,并将数据扁平化处理展开为9216个单元
第六层、第七层和第八层(全连接层):全连接加上Softmax分类器输出1000类的分类结果,有将近6千万个参数
VGGNet
GGNet由牛津大学和DeepMind公司提出
- Visual Geometry Group:https://www.robots.ox.ac.uk/~vgg/
- DeepMind:https://deepmind.com/
它的特点是:
- 比较常用的是VGG-16,结构规整,具有很强的拓展性
- 相较于AlexNet,VGG-16网络模型中的卷积层均使用 3∗3 的 卷积核,且均为步长为1的same卷积,池化层均使用 2∗2 的 池化核,步长为2
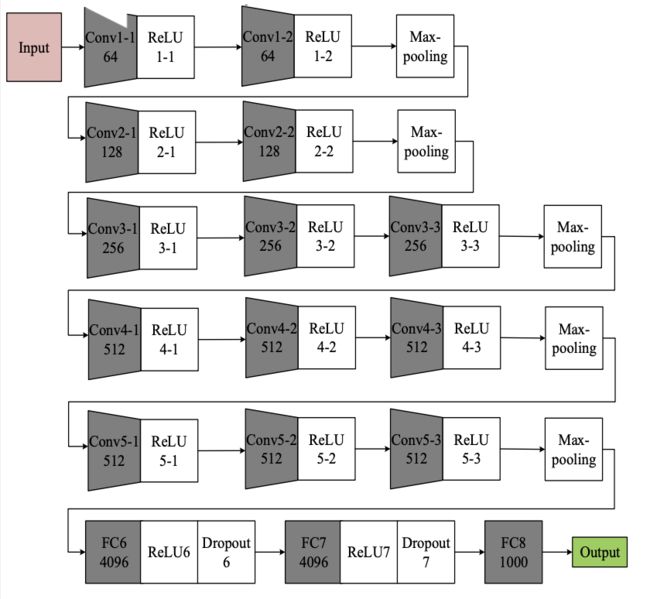
网络结构
- 两个卷积核大小为3∗3 的卷积层串联后的感受野尺寸为 5∗5, 相当于单个卷积核大小为 5*55∗5 的卷积层
- 两者参数数量比值为(2∗3∗3)/(5∗5)=72% ,前者参数量更少
- 此外,两个的卷积层串联可使用两次ReLU激活函数,而一个卷积层只使用一次
Inception Net
Inception Net 是Google公司2014年提出,获得ImageNet LSVRC-2014冠军。文章提出获得高质量模型最保险的做法就是增加模型的深度(层数)或者是其宽度(层核或者神经元数),采用了22层网络。
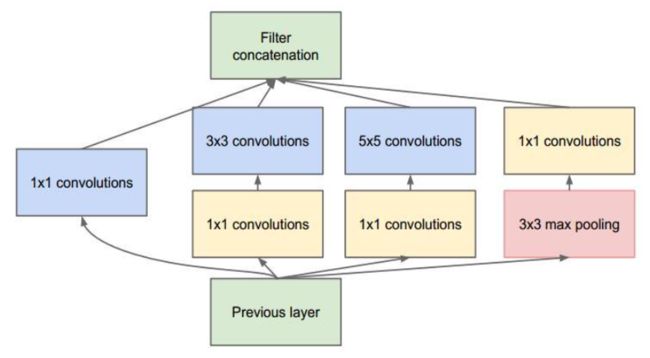
Inception Module
- 深度:层数更深,采用了22层,在不同深度处增加了两个 loss来避免上述提到的梯度消失问题
- 宽度:Inception Module包含4个分支,在卷积核3x3、5x5 之前、max pooling之后分别加上了1x1的卷积核,起到了降低特征图厚度的作用
- 1×1的卷积的作用:可以跨通道组织信息,来提高网络的表达能力;可以对输出通道进行升维和降维。
ResNet
ResNet(Residual Neural Network),又叫做残差神经网 络,是由微软研究院的何凯明等人2015年提出,获得ImageNet ILSVRC 2015比赛冠军,获得CVPR2016最佳论文奖。
随着卷积网络层数的增加,误差的逆传播过程中存在的梯 度消失和梯度爆炸问题同样也会导致模型的训练难以进行,甚至会出现随着网络深度的加深,模型在训练集上的训练误差会出现先降低再升高的现象。残差网络的引入则有助于解决梯度消失和梯度爆炸问题。
残差块
ResNet的核心是叫做残差块(Residual block)的小单元, 残差块可以视作在标准神经网络基础上加入了跳跃连接(Skip connection)
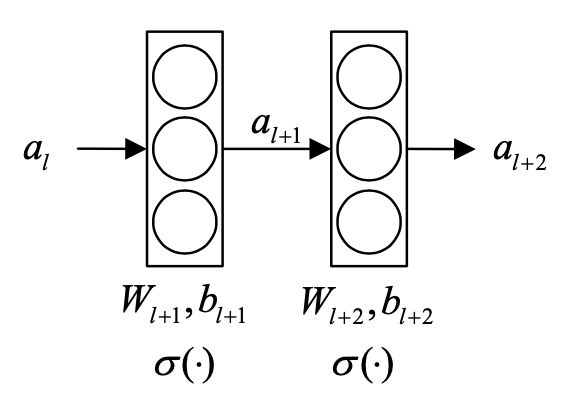
- 原连接
a l + 1 = σ ( W l + 1 a + b l + 1 ) a l + 2 = σ ( W l + 2 a l + 1 + b l + 2 ) a_{l+1}=\sigma(W_{l+1}a + b_l+1) \\ a_{l+2}=\sigma(W_{l+2}a_{l+1}+b_{l+2}) al+1=σ(Wl+1a+bl+1)al+2=σ(Wl+2al+1+bl+2)
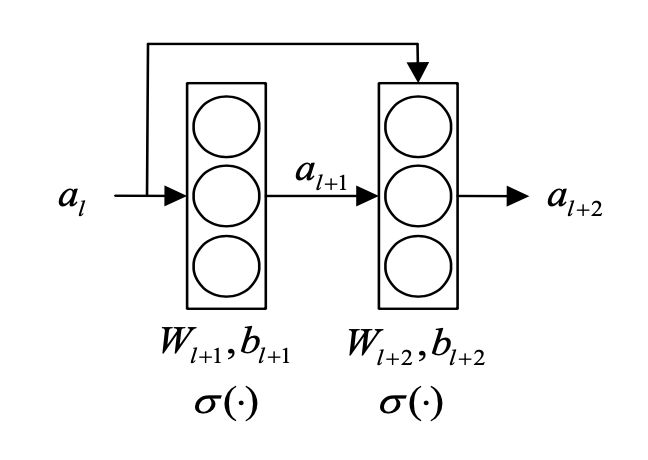
- 跳跃连接
a l + 1 = σ ( W l + 1 a l + b l + 1 ) a l + 2 = σ ( W l + 2 a l + 1 + b l + 2 + a l ) a_{l+1}=\sigma(W_{l+1}a_l+b_{l+1})\\ a_{l+2}=\sigma(W_{l+2}a_{l+1}+b_{l+2}+a_l) al+1=σ(Wl+1al+bl+1)al+2=σ(Wl+2al+1+bl+2+al)
Skip connection的作用
记
u l + 1 = W l + 1 a l + b l + 1 , u l + 2 = W l + 2 a l + 1 + b l + 2 + a l = u ^ l + 2 + a l u_{l+1}=W_{l+1}a_l+b_{l+1},u_{l+2}=W_{l+2}a_{l+1}+b_{l+2}+a_l=\widehat{u}_{l+2}+a_l ul+1=Wl+1al+bl+1,ul+2=Wl+2al+1+bl+2+al=u l+2+al
我们有
KaTeX parse error: No such environment: align at position 8: \begin{̲a̲l̲i̲g̲n̲}̲ \frac{\partial…
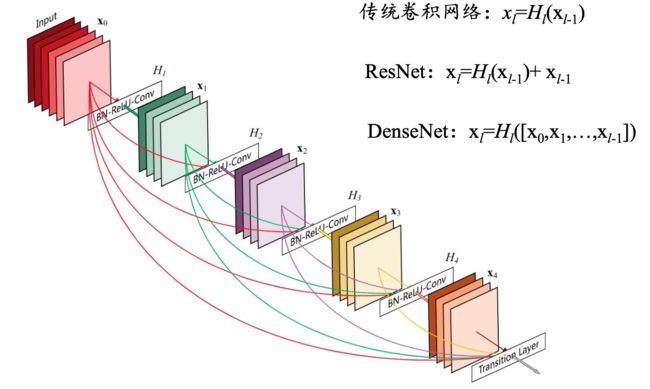
Densenet
DenseNet中,两个层之间都有直接的连接,因此该网络的直接连接个数为L(L+1)/2。
对于每一层,使用前面所有层的特征映射作为输入,并且使用其自身的特征映射作为所有后续层的输入
5层的稠密块示意图
DenseNets可以自然地扩展到数百个层,而没有表现出优化困难。在实验中,DenseNets随着参数数量的增加,在精度上产生一致的提高,而没有任何性能下降或过拟合的迹象。
优点
- 缓解了消失梯度问题
- 加强了特征传播,鼓励特征重用
- 一定程度上减少了参数的数量
主要应用
图像处理领域主要应用
- 图像分类(物体识别):整幅图像的分类或识别
- 物体检测:检测图像中物体的位置进而识别物体
- 图像分割:对图像中的特定物体按边缘进行分割
- 图像回归:预测图像中物体组成部分的坐标
语音识别领域主要应用
自然语言处理领域主要应用
情感分析:分析文本体现的情感(正负向、正负中或多态度类型)
参考:(Yoon Kim)Convolutional Neural Networks for Sentence https://arxiv.org/abs/1408.5882
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-7fCi3OX1-1638018363678)(https://datawhalechina.github.io/unusual-deep-learning/PIC/5/5.21.png)]
参考资料:datawhale