吐血整理-人工智能必备数学基础(五)
导读:数学基础知识蕴含着处理智能问题的基本思想与方法,也是理解复杂算法的必备要素。今天的人工智能技术归根到底都建立在数学模型之上
下面是整理的其他文章,希望对大家有所帮助,点击即可阅读
人工智能常用的十大算法
人工智能必备数学基础(一)
人工智能数学基础(二)
强烈建议配合课件资料一起学习!效果最好!
为了方便大家学习交流,我建了一个扣裙:966367816(学习交流、大牛答疑、大厂内推)
另外我还整理了整整200G的人工智能学习笔记、课程视频、面试宝典一并可以无套路免费
分享给大家!
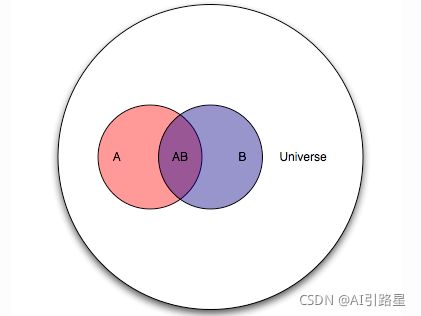
贝叶斯分析
解释:
经典的概率论对小样本事件并不能进行准确的评估,若想的到相对准确的结论往往需要大量的现场实验,而贝叶斯理论能较好的解决这一问题,利用已有的先验信息,可以得到分析对象准确的后验分布,贝叶斯模型是用参数来描述的,并且用概率分布描述这些参数的不确定性。
贝叶斯分析的思路由证据的积累来推测一个事物发生的概率,它告诉我们当我们要预测一个事物需要的是首先根据已有的经验和知识推断一个先验概率,然后在新证据不断积累的情况下调整这个概率。整个通过积累证据来得到一个事件发生概率的过程我们称为贝叶斯分析。
方法:
贝叶斯推断的基本方法是将关于未知参数的先验信息与样本信息综合,再根据贝叶斯定理,得出后验信息,然后根据后验信息去推断未知参数
1、客观贝叶斯分析(objective Bayesian analysis):
客观贝叶斯学派的主要内容是使用无信息先验分布(noninformativeor default prior distribution),另一个完全不同的领域是研究对"默认"模型(defaultmodel)的选择和假设检验。
经常使用非正常先验分布(improper priordistribution)也是客观贝叶斯学派面临的主要问题,这不能满足贝叶斯分析所要求的一致性(coherency)。同样,一个选择不适当的非正常先验分布可能会导致一个非正常的后验分布,这就要求贝叶斯分析过程中特别要对此类问题加以重视,以避免上述问题的产生。同样,客观贝叶斯学派也经常从非贝叶斯的角度进行分析,而且得出的结果也非常有效。
2、主观贝叶斯分析(subjective Bayesian analysis )
使用主观贝叶斯先验分布信息是非常必要的,而且也容易被其他人所接受。对这些问题使用主观贝叶斯分析可以获得令人惊奇的结论。即使当研究某些问题时,如使用完全的主观分析不可行,那么同时使用部分的主观先验信息和部分的客观先验信息对问题进行分析,这种明智的选择经常可以取得很好的结果(Andrews,Berger and Smith,1993)。
3、稳健贝叶斯分析(robust Bayesian analysis )
稳健贝叶斯分析研究者认为,不可能对模型和先验分布进行完全的主观设定,即使在最简单的情况下,完全主观设定也必须包含一个无穷数。稳健贝叶斯的思想是构建模型与先验分布的集合,所有分析在这个集合框架内进行,当对未知参数进行多次推导(elicitation )之后,这个集合仍然可以反映此未知参数的基本性质。
关于稳健贝叶斯分析基础的争论是引人注目的(Kadane,1984;Walley,1991),关于稳健贝叶斯分析最新进展的文献可参见伯杰(Bergen1985,1994,1996)的研究。通常的稳健贝叶斯分析的实际运用需要相应的软件。
4、频率贝叶斯分析(frequentist Bayesian analysis )
贝叶斯语言既可对主观的统计学进行分析,又可以对客观的统计学进行分析。第二,从方法论角度来看,对参数问题的求解,贝叶斯分析具有明显的方法论上的优势。当然,频率的概念也是非常有用的,特别是在确定一个好的客观贝叶斯过程方面。第三,从频率学派的观点看来,基础统一应该是必然的。我们早就认识到贝叶斯方法是"最优"的非条件频率方法(Berger,1985),现在从条件频率方法的角度,也产生了许多表明以上结论正确的依据。
5、拟(准)贝叶斯分析(quasi Bayesian analysis )
拟(准)贝叶斯方法,伴随着MCMC方法的发展,已经被证明是一种非常有效的方法,这种方法可以在使用过程中,不断产生新的数据和知识。虽然拟(准)贝叶斯方法还存在许多不足,但拟(准)贝叶斯方法非常容易创造出一些全新的分析过程,这种分析过程可以非常灵活地对数据进行分析,这种分析过程应该加以鼓励。对这种分析方法的评判,不必要按照贝叶斯内在的标准去衡量,而应使用其他外在的标准去判别(例如敏感性、模拟精度等)。
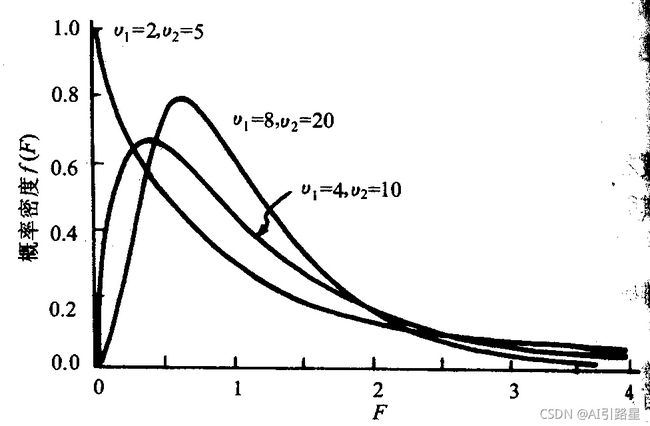
方差分析
方差分析(Analysis of Variance,简称ANOVA),又称"变异数分析"或"F检验",是R.A.Fisher发明的,用于两个及两个以上样本均数差别的显著性检验。 由于各种因素的影响,研究所得的数据呈现波动状。造成波动的原因可分成两类,一是不可控的随机因素,另一是研究中施加的对结果形成影响的可控因素。
方差分析是从观测变量的方差入手,研究诸多控制变量中哪些变量是对观测变量有显著影响的变量。
分析方法:
根据资料设计类型的不同,有以下两种方差分析的方法:
1、对成组设计的多个样本均值比较,应采用完全随机设计的方差分析,即单因素方差分析。
2、对随机区组设计的多个样本均值比较,应采用配伍组设计的方差分析,即两因素方差分析。
整个方差分析的基本步骤如下:
1、建立检验假设;
H0:多个样本总体均值相等;
H1:多个样本总体均值不相等或不全等。
检验水准为0.05。
2、计算检验统计量F值;
3、确定P值并作出推断结果。
主要作用:
一个复杂的事物,其中往往有许多因素互相制约又互相依存。方差分析的目的是通过数据分析找出对该事物有显著影响的因素,各因素之间的交互作用,以及显著影响因素的最佳水平等。方差分析是在可比较的数组中,把数据间的总的“变差”按各指定的变差来源进行分解的一种技术。对变差的度量,采用离差平方和。方差分析方法就是从总离差平方和分解出可追溯到指定来源的部分离差平方和,这是一个很重要的思想。
经过方差分析若拒绝了检验假设,只能说明多个样本总体均值不相等或不全相等。若要得到各组均值间更详细的信息,应在方差分析的基础上进行多个样本均值的两两比较。
多个样本均值间两两比较
多个样本均值间两两比较常用q检验的方法,即Newman-kueuls法,其基本步骤为:建立检验假设-->样本均值排序-->计算q值-->查q界值表判断结果。
多个实验组与一个对照组均值间两两比较
多个实验组与一个对照组均值间两两比较,若目的是减小第II类错误,最好选用最小显著差法(LSD法);若目的是减小第I类错误,最好选用新复极差法,前者查t界值表,后者查q'界值表。
聚类分析
聚类分析指将物理或抽象对象的集合分组为由类似的对象组成的多个类的分析过程。它是一种重要的人类行为。
聚类分析的目标就是在相似的基础上收集数据来分类。聚类源于很多领域,包括数学,计算机科学,统计学,生物学和经济学。在不同的应用领域,很多聚类技术都得到了发展,这些技术方法被用作描述数据,衡量不同数据源间的相似性,以及把数据源分类到不同的簇中。
定义:
依据研究对象(样品或指标)的特征,对其进行分类的方法,减少研究对象的数目。
各类事物缺乏可靠的历史资料,无法确定共有多少类别,目的是将性质相近事物归入一类。
各指标之间具有一定的相关关系。
聚类分析(cluster analysis)是一组将研究对象分为相对同质的群组(clusters)的统计分析技术。 聚类分析也叫分类分析(classification analysis)或数值分类(numerical taxonomy)
变量类型:定类变量、定量(离散和连续)变量
聚类与分类的不同在于,聚类所要求划分的类是未知的。
概念:
聚类是将数据分类到不同的类或者簇这样的一个过程,所以同一个簇中的对象有很大的相似性,而不同簇间的对象有很大的相异性。
从统计学的观点看,聚类分析是通过数据建模简化数据的一种方法。传统的统计聚类分析方法包括系统聚类法、分解法、加入法、动态聚类法、有序样品聚类、有重叠聚类和模糊聚类等。采用k-均值、k-中心点等算法的聚类分析工具已被加入到许多著名的统计分析软件包中,如SPSS、SAS等。
从机器学习的角度讲,簇相当于隐藏模式。聚类是搜索簇的无监督学习过程。与分类不同,无监督学习不依赖预先定义的类或带类标记的训练实例,需要由聚类学习算法自动确定标记,而分类学习的实例或数据对象有类别标记。聚类是观察式学习,而不是示例式的学习。
从实际应用的角度看,聚类分析是数据挖掘的主要任务之一。而且聚类能够作为一个独立的工具获得数据的分布状况,观察每一簇数据的特征,集中对特定的聚簇集合作进一步地分析。聚类分析还可以作为其他算法(如分类和定性归纳算法)的预处理步骤。
应用:
在商业上被用来发现不同的客户群,并且通过购买模式刻画不同的客户群的特征。
是细分市场的有效工具,同时也可用于研究消费者行为,寻找新的潜在市场、选择实验的市场,并作为多元分析的预处理。
在生物上被用来动植物分类和对基因进行分类,获取对种群固有结构的认识
在地理上能够帮助在地球中被观察的数据库商趋于的相似性
在保险行业上通过一个高的平均消费来鉴定汽车保险单持有者的分组,同时根据住宅类型,价值,地理位置来鉴定一个城市的房产分组
在因特网应用上被用来在网上进行文档归类来修复信息
在电子商务中网站建设数据挖掘中也是很重要的一个方面,通过分组聚类出具有相似浏览行为的客户,并分析客户的共同特征,可以更好的帮助电子商务的用户了解自己的客户,向客户提供更合适的服务。
回归分析
相关分析是研究两个或两个以上的变量之间相关程度及大小的一种统计方法
回归分析是寻找存在相关关系的变量间的数学表达式,并进行统计推断的一种统计方法
在对回归分析进行分类时,主要有两种分类方式:
●根据变量的数目,可以分类一元回归、多元回归
●根据自变量与因变量的表现形式,分为线性与非线性
所以,回归分析包括四个方向:一-元线性回归分析、多元线性回归分析、一-元非线性回归分析、多元非线性回归分析。
相关应用:
相关分析研究的是现象之间是否相关、相关的方向和密切程度,一般不区别自变量或因变量。而回归分析则要分析现象之间相关的具体形式,确定其因果关系,并用数学模型来表现其具体关系。比如说,从相关分析中我们可以得知“质量”和“用户满意度”变量密切相关,但是这两个变量之间到底是哪个变量受哪个变量的影响,影响程度如何,则需要通过回归分析方法来确定。
一般来说,回归分析是通过规定因变量和自变量来确定变量之间的因果关系,建立回归模型,并根据实测数据来求解模型的各个参数,然后评价回归模型是否能够很好的拟合实测数据;如果能够很好的拟合,则可以根据自变量作进一步预测。
相关分析
相关分析:
●衡量事物之间或称变量之间线性相关程度的强弱,并用适当的统计指标表示出来的过程。
●比如,家庭收入和支出、一个人所受教育程度与其收入、子女身高和父母身高等
相关系数:
, 衡量变量之间相关程度的一个量值
●相关系数r的数值范围是在-1到十1之间
●相关系数r的正负号表示变化方向。“+”号表示变化方向一致,即正相关;“-” 号表示变化方向相反,即负相关
●r的绝对值表示变量之间的密切程度(即强度)。 绝对值越接近1,表示两个变量之间关系越密切;越接近0,表示两个变量之间关系越不密切
●相关系数的值,仅仅是一个比值。它不是由相等单位度量而来(即不等距), 也不是百分比,因此,不能直接作加、减、乘、除运算
相关系数只能描述两个变量之间的变化方向及密切程度,并不能揭示两者之间的内在本质联系,即存在相关的两个变量,不一定存在因果关系
(搭配源码视频更佳哦~可以找我下载的)
需要课件配套课件资料和源码笔记的伙伴加我微信免费领取!
为了方便大家学习交流,我建了一个扣裙:966367816学习交流、大牛答疑、大厂内推)
另外我还整理了整整200G的人工智能学习笔记、课程视频、面试宝典
一并可以无套路免费分享给大家!
欢迎大家来撩我呀~
![]()