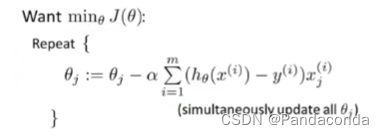【吴恩达机器学习笔记】五、逻辑回归
✍个人博客:https://blog.csdn.net/Newin2020?spm=1011.2415.3001.5343
专栏定位:为学习吴恩达机器学习视频的同学提供的随堂笔记。
专栏简介:在这个专栏,我将整理吴恩达机器学习视频的所有内容的笔记,方便大家参考学习。
视频地址:吴恩达机器学习系列课程
❤️如果有收获的话,欢迎点赞收藏,您的支持就是我创作的最大动力
五、逻辑回归
1. 逻辑回归
接下来我们要讲的是关于分类的算法,可以大致分为两个部分,首先要讲的是第一个部分只有两个标签的分类,后面我们会讲到第二部分多标签的分类。
只有两个标签的分类应该很好理解,无非就是将两个类别放在计算机中就变成了判断0和1,0我们就称为负样本(Negative Class),而1我们就称为正样本(Positive Class)。
下面我们举个例子,用线性回归来进行分类,看看效果如何。
我们可以看到,通过输入样本,计算机就会自动拟合出一条曲线,阈值在0.5的地方,这样看起来效果似乎不错,但是有没有想过,如果有个样本特立独行远离了这些“大群体”,那这条曲线会受到什么影响。
可以看到,整条曲线因为一个样本,与原有曲线相差甚大,所以我们一般不会用线性回归进行分类,不光是因为上面这个例子,它还有一个让人琢磨不透的地方就是,即使你输入的样本都是0或1,它的预测值竟然会大于1或者小于0。基于上面这些问题,接下来的主角就登场了,下面将会用到Logistic回归去进行分类。
名字看起来是用来解决关于回归的问题,但实际上它是一种分类算法,这是因为一些历史原因所致。
逻辑回归(Logistic Regression)模型
这个模型所用的函数是Sigmoid function(Logistic function),而Sigmoid funciton得到的的结果都会分布在0和1之间,公式如下:
下面我将给出这个模型的解释。
我们可以假设hθ(x)代表输入值是x且y=1的概率,上面就是一个例子,可以看到输入x1后,hθ(x)=0.7即当x1输入后,有70%的概率是恶性肿瘤。
并且我们还有一点需要注意,P(y = 1|x;θ)代表的意思是在x的情况下,参数是θ且y=1的概率。
我们再对上面进行一下小结,我们可以设定一个规则,当hθ(x)≥0.5时,y=1,并且通过图像观察可以得到θTx≥0;相反当hθ(x)<0.5时,y=0,并且可以得到θTx<0。
2. 决策界限
决策边界(Decision Boundary)
这个决策边界就是上图的那条红线,用来划分y=1和y=0的界限,由g中的函数公式得到,上面例子得到的边界是线性的。
但是如果特征变多了,决策边界就不像一条直线那么简单,它可能就是非线性的曲线了,就如下面这个例子:
小结
决策边界与之前的线性回归不同,它的曲线并不是由给出的数据集所决定,而是当θ给出后,它就已经决定了。
3. 代价函数
在做完上面的铺垫后,这节课要讲的就是在其他条件都给定的情况下,如何得到θ值。
Logistic回归代价函数
从这个公式可以看出,代价函数中当y=1和当y=0时的式子不太一样,我们先来看当y=1时的情况。
你会发现在y=1的情况下,当hθ(x)等于1时cost为0,这就是我们想得到的结果,反过来当hθ(x)为0时,cost根本得不到值,并且hθ(x)趋近于0时,cost会非常的大从而被排除,所以就能得到到hθ(x)=0时y不可能为1的结果。接下来再来看看当y=0时的情况。
从图中可以看到,y=0的图像与y=1的图像对称,所以得到的结论也是完全相反,即当hθ(x)=0时,cost为0是最小的,而当hθ(x)等于1时,cost同样也取不到,hθ(x)趋向1时cost也会变得非常的大从而被排除,所以就能得到hθ(x)=1时y不可能为0的结果。
从上面来看,我们就能理解为什么当y=0时hθ(x)<0.5而当y=1时hθ(x)≥0.5了。
接下来,我将为你介绍如何去简化上面代价函数的式子,如下:
你可以将y=0和y=1的情况带入式子,就可以得到一个整合的式子,我们可以验证一下,当把y=1和y=0分别带入这个式子可以得到两个式子,跟上面提到的两个式子完全相同,因为y和1-y总有一边会消为0。
所以弄清楚其中原理后,我们就要像之前一样,要去找到θ的最优值即当J(θ)最小时候的θ。
而我们现在又可以用到梯度下降的算法来计算θ的最优值。
将式子带入,化简之后得:
到这里你可能会有疑问,这不是跟之前线性回归的梯度下降公式一毛一样吗,但实际上并不是,因为logistic回归的假设函数h(θ)与线性回归的完全不一样,所以带入式子会得到两个不一样的结果。但是因为两者都是用到了梯度下降算法,所以两者的特征值如果相差过大,都可以用特征缩放来缩小特征值,从而使梯度下降收敛更快。
小结
logistic回归是一种非常强大,甚至是全世界运用最广泛的一种分类算法。
4. 高级优化
上面我们是通过给到θ然后计算J(θ)以及它对θ的偏导数值然后带入梯度下降的算法得到最优值,但是当数据变得非常多时,梯度下降的效率就会大打折扣,所以还有其他更好的算法可以计算θ最优值时收敛的更快,但同时也会更加复杂。
如上面所示,共轭梯度算法(Conjugate gradient)、BFGS和L-BFGS三个算法收敛的速度会更快,而且你不用手动的去计算α,他们会自动计算给出最优α,但是缺点就是太过于复杂。现实中,不用去深入了解这些算法的细节,除非你是数值专家,你只需要知道怎么去用,怎么写代码就够了。
而总结起来就是首先我们要给出θ的值,然后写出代价函数的代码区计算J(θ)与其对θ的偏导数,然后用高级优化算法去得出最优解。
5. 多元分类
接下来我们来讲讲用逻辑回归来进行多分类,下面举几个例子来解释什么是多分类:
你可以将它想象成你有一个邮件,它可以自动的去分到工作、朋友、家人和爱好其中的类别当中,这就是多分类问题,当然你也可以想象成其它例子,就如上面的看病或者天气例子,所以在图像上也会有所不同。
我们就拿三元分类作为例子:
我们可以将三个类别分别设为y=1、y=2和y=3,然后得出三个分类器,每一个拟合器对应着一个类别,分别对每个分类器进行训练,然后测量对应类别的概率。
小结
一对多的分类问题,就是通过对每一个类别训练一个分类器,分别得到不同的h(θ),这样当输入x的时候,我们就将x分别输入每一个分类器进行计算其概率值,最终h(θ)值最大的那个分类器所对应的类别即是我们要分入的类别。