训练后量化(PTQ) 工作流理解
目前神经网络在许多前沿领域的应用取得了较大进展,但经常会带来很高的计算成本,对内存带宽和算力要求高。另外降低神经网络的功率和时延在现代网络集成到边缘设备时也极其关键,在这些场景中模型推理具有严格的功率和计算要求。神经网络量化是解决上述问题有效方法之一,但是模型量化技术的应用会给模型带来额外噪音,从而导致精度下降,因此工程师对模型量化过程的理解有益于提高部署模型的精度。本文主要介绍训练后量化 (Post-training quantization,PTQ) 的关键基础技术,首先介绍了 PTQ 的定义、量化的数学定义即量化公式、量化模拟、range setting,最后介绍了 PTQ 的整体技术流程。
0. PTQ
训练后量化 (PTQ) 算法将训练过的 FP32 网络直接转换为定点计算的网络,过程中无需对原始模型进行任何训练。只对几个超参数调整就可完成量化过程,量化模型以一种更有效的计算方式进行模型推理。量化后模型中的参数使用低 bit 表示,在数据搬移时降低了带宽要求,在计算过程中一般硬件对于低 bit 整形数据具有更高的标称算力,因此模型量化的优化方案在多数情况下可获得较大的推理速度提升,此方法已被广泛应用于大量的端侧和云侧部署场景。
1. Uniform affine quantization
量化一般是指将 32bit 存储的数据映射为 低 bit 整形数据,量化后可以借助于硬件对低 bit 数据的计算优势对神经网络平算子进行加速计算。在现有的量化方法中,工程化时一般使用均匀量化,这样更有益于底层硬件对低 bit 数据进行计算优化。均匀量化有两种情况,分别为非对称量化和对称量化,其中对称量化是非对称量化的一个特例,本文不再讲述。
仿射量化也称为非对称量化,其由三个参数定义,分别为 s(scale factor)、z( zero-point)、b(bit-width) 。使用 s 和 z 将浮点值映射到整数,整数的范围则取决于位宽 b 。scale factor 一般由浮点值表示,其表明了量化过程的步长 。zero-point 是一个整数,其保证真正的零点可以无误差映射到整形数据,该参数对于 zero padding 和 relu 激活函数的计算具有重要意义。
一旦三个量化参数确定了,我们就可以使用量化操作了,将一个浮点类型的 vector X 映射到无符号整形 。
402 Payment Required
表示 round-to-nearest 算子,clamp 函数表示如下:
402 Payment Required
使用反量化表示真实值的估计值如下:
组合上述两个步骤可以获得通用量化函数定义 :
通过反量化步骤,我们可以定义量化范围 ,其中 、 。任何超出量化范围的数值将被被截断,产生 clipping error 。我们可以通过增大量化的范围减小 clipping error ,但是会增加 scale factor ,从而导致 round error 增加, round error 为 。因此量化参数的选择过程就是 round error 和 clipping error 平衡的过程。
通过上述量化方案我们就可以将模型中的 weight 和 activation 从浮点值映射到低 bit 整形数据,但二者也有所不同, weight 一般是提前量化好的, activation 依赖于模型的输入数据,是在模型进行推理时生成的,因此 activation 的量化需要少量的校准数据集。
2. Quantization simulation
为了测试一个模型量化后运行的效果,一般都是在相同的通用硬件上进行量化行为仿真,该过程称为量化模拟。使用浮点算子操作来近似量化算子操作,量化模拟主要用来减少仿真和实际硬件运行的误差。
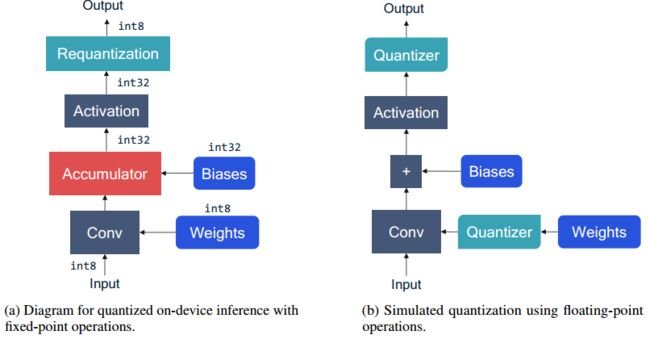
下图 a 中表示了卷积层的定点量化计算过程。计算过程中 biases、weight、input activations 全部为定点格式。但是仿真过程中全部使用浮点类型数据,这样就可以使用量化器来指导量化过程。下图 b 中展示了卷积层在通用框架中的仿真模型,在 weight 和 conv 之间插入量化器(Quantizer)来模拟 weight 的量化,在 activation function 后插入量化器来模拟 activation 量化。bias 一般使用高精度保存。量化器一般由 scale factor, zero-point, bit-width 三个元素确定,量化器的 input 和 output 都是 float32 格式,但是最终的 output 的大小位于量化网格上。
图1 conv 层的前向推理过程. a 图表示实际量化推理. b 图表示通用 fp32 硬件实现的量化模拟3. Quantization range setting
Range setting 是指在量化过程中针对原来 tensor 各元素的数值范围进行截断的过程,找到所有元素的最大值和最小值,记为 、 ,量化的关键是 round error 和 clip error 的平衡过程,当范围设置较大时,clip error 小 round error 大,当范围设置小时,结果相反。但是 tensor 中的各元素有时会出现一些异常离群点,如果为了包含这些离群点将截断范围划分较大,将造成 round error 增加,因此下面描述的 Min-max 、Mse 方法提供了不同的权衡策略。这些方法通常使用优化局部 loss 函数找到最优。因为在 PTQ 中,使用快速计算的方法,而不是做端到端的训练。weight 通常在不需要校准数据的情况下进行量化,由于激活函数值依赖于输入数据,因此激活函数的量化参数通常需要少量校准数据。
Min-max: 为了覆盖张量的整个动态范围,我们可以定义量化参数如下:
其中 V 表示要量化的张量。这不会导致 clip error 。这种方法对异常值很敏感,因为幅值较大异常值可能会导致过大的 round error 。
Mean squared error(MSE): 缓解大异常值问题的一种方法是使用基于 MSE的 range setting 。通过寻找损失函数的最小值,来确定 、 。
指的是 的量化版本, 是 Frobenius norm ,一般这个优化问题使用 grid search 等方法完成。
4. PTQ的总体技术路线:
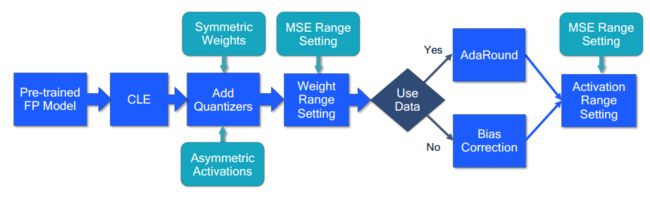
上文主要讲述了量化公式、量化模拟、range setting 等基础量化关键技术,但是只使用这些技术仍然不能获得较好性能的模型,仍然会存在一些其他的问题,例如,神经网络层中权重各元素幅值相差较大,直接量化将会产生较大的 round error,缺少校准数据集等问题。通过多种技术对量化模型进行矫正,在视觉模型和 NLP 模型上都可以取得性能优益的量化模型。因此下面给出了 PTQ的总体技术路线如下图所示:
Cross-layer equalization:
应用跨层均衡(CLE),主要是解决权重矩阵中的各元素幅值差别较大的问题,其主要思路是提取缩放因子矩阵,将缩放因子矩阵传递到下一层上去计算,该预处理应用于全精度模型,使其对模型量化更加友好。CLE 特别对 depth-wise 层和 per-tensor 量化很重要,但通常对其他层和量化策略选择也有所改善。
Add quantizers:
在网络中添加量化器,通常称为量化模拟,量化器主要为了测试神经网络在量化设备上的运行情况,对量化误差进行评价。量化器的选择可能取决于特定的目标硬件,对于常见的 AI 加速器,建议对权重使用对称量化器和对激活函数使用非对称量化器。
Weight range setting:
在对 weight 进行 range setting 时,一般建议使用基于 MSE 的标准。在 per-channel 量化的情况下,使用 Min-Max 方法可能获得更好的效果。
AdaRound:
如果有一个较小的校准数据集可用,可以使用 AdaRound 优化方法选择 weight 的 round 策略。这一步对于超低 bit(例如 4bit )量化至关重要。
Bias correction:
如果没有校准数据集并且网络使了 Batch Norm,可以使用分析方法进行偏差校正
Activation range setting:
激活的 range setting 是 PTQ 的最后一步,针对所有依赖于 data 的 tensor 进行 range setting。对于大多数层使用MSE标准进行 range setting,需要少量的校准数据集来计算最小的 MSE loss 。另外对于 BN 层可以使用无需数据的方法进行设置。
图2 标准 PTQ 工作流 蓝框表示必要步骤,绿框表示选择步骤
实验效果
对多个模型进行 PTQ 量化的结果如下表所示,可以看出 8 bit 量化的 weight 和 activation (W8A8) 的情况下,模型正确率下降较小,相比于 float32 模型模型正确率下降控制在 0.7% 以内。当使用 8 bit 量化时,per-channel 的量化方式并没有较为明显的收益。但是在超低 bit 如 W4A8 的情况下 MobileNetV2、EfficientNet lite 的 per-tensor 量化分别下降了 2.5% 和 4.2%,主要是因为这两个模型中存在较多的 depth-wise 卷积层,但是 per-tensor 的量化方式对于底层的计算优化可以带来较大收益,因此在面对这样的状况时,PTQ 量化技术不能满足用户需求。
图3 基于 PTQ 量化方法各模型的正确率结论
PTQ 量化技术是首先需要考虑使用的优化工具,因为该技术可在不需要标签数据和重新训练的情况下,快速高效的实现。然而,该技术也有其局限性,有时不能获得较高的模型正确率,尤其当使用超低 bit 的激活函数量化时,很有可能不能够获取较好效果。因此在量化模型精度不足,并且有带标签数据和足够时间去重新训练量化模型时,可以使用量化感知训练(QAT)的方法进行模型量化的探索,来提高模型正确率。
欢迎点击“阅读原文”,关注Adlik Github仓库。
参考文献
[1] Markus Nagel, Marios Fournarakis, Rana Ali Amjad, Yelysei Bondarenko, Mart van Baalen, Tijmen Blankevoort.A White Paper on Neural Network Quantization