机器学习中的损失函数（交叉熵损失、Hinge loss）

损失函数

1 交叉熵损失

1.1 从最大似然估计到交叉熵损失

概率论中的MLE

最大似然估计用于估计能得到当前数据（分布）的最好的参数组合。对于最简单的x为一维的概率分布我们有
$${\hat{\theta }}_{MLE}=\underset{\theta }{\mathrm{argmax}}{f}_X(x_1,x_2,...,x_n;\theta )=\underset{\theta }{\mathrm{argmax}}\prod _i{f}_X(x_i;\theta )$$
**maximum likelihood estimate (MLE)**是要找使得似然函数最大的参数，而似然函数是数据的pdf即概率密度函数的乘积。我们希望找到这样的参数使得出现我们现在拿到的这一组数据$\{x_1,x_2,...,x_n\}$的可能性最大，这里可能性我们用pdf来衡量。

PDF：概率密度函数（probability density function）, 连续型随机变量的概率密度函数是一个描述某个确定的取值点附近的可能性的函数。

机器学习中的MLE

机器学习中的二分类任务，对于有**真实标签$y_1,y_2,...,y_n,y_i\in \{0,1\}$**的数据$\{x_1,x_2,...,x_n\}$，我们可以将这些数据看成来自不同伯努利分布的数据，即$y_i\sim B(1,p_i)$，我们获得尽量准确的每个数据$x_i$来自类别1的努利分布概率，也即找到所有参数$p_1,p_2,...,p_n$，使得在这样的分布下，出现$y_1,y_2,...,y_n,y_i\in \{0,1\}$这种真实数据的情况的可能性最大（可能性最大这里即是“似然”的思想）。
$$\begin{gathered} {\hat{p}}_1,{\hat{p}}_2,...,{\hat{p}}_n=\underset{p_1,p_2,...,p_n}{\mathrm{argmax}}{f}_X(y_1,y_2,...,y_n;p_1,p_2,...,p_n) \\ =\underset{p_1,p_2,...,p_n}{\mathrm{argmax}}\prod _i{f}_X(y_i;p_i) \\ =\underset{p_1,p_2,...,p_n}{\mathrm{argmax}}\prod _i{p}_i^{y_i}(1-p_i{)}^{1-y_i} \end{gathered}$$
而每个数据$x_i$来自类别1的概率$p_i$，则与通过其他方法得到的$y_i$的预测值${\hat{y}}_i$有关，即对于每个数据$x_i$，我们会得到预测值${\hat{y}}_i$对应为两类别的概率，即
$$\begin{gathered} \mathbb{P}[{\hat{y}}_i=1]=p_i \\ \mathbb{P}[{\hat{y}}_i=0]=1-p_i \end{gathered}$$
所以现在问题其实变化成了我们要去找到最好的预测结果$\{{\hat{y}}_i,{\hat{y}}_2,...,{\hat{y}}_n\}$，这也就是机器学习方法的“打标签”的目标
$${\hat{y}}_i,{\hat{y}}_2,...,{\hat{y}}_n=\underset{{\hat{y}}_i,{\hat{y}}_2,...,{\hat{y}}_n}{\mathrm{argmax}}\prod _i(\mathbb{P}[{\hat{y}}_i=1]{)}^{y_i}(1-\mathbb{P}[{\hat{y}}_i=1]{)}^{1-y_i}$$
记似然函数为
$$\begin{gathered} \mathcal{L}=\prod _i(\mathbb{P}[{\hat{y}}_i=1]{)}^{y_i}(1-\mathbb{P}[{\hat{y}}_i=1]{)}^{1-y_i} \\ \Rightarrow \log \mathcal{L}=\sum _i{y}_i\log (\mathbb{P}[{\hat{y}}_i=1])+(1-y_i)\log (1-\mathbb{P}[{\hat{y}}_i=1]) \end{gathered}$$
则我们的目标是要最大化$\log \mathcal{L}$.

在这个基础上，考虑我们机器学习中的方法常常表述为“最小化loss损失”，所以我们对似然函数取负号，得到loss的形式
$$loss=-\sum _i{y}_i\log (\mathbb{P}[{\hat{y}}_i=1])+(1-y_i)\log (1-\mathbb{P}[{\hat{y}}_i=1])$$
另外常常需要对结果作一个归一化，所以除以总的样本数，得到
$$\begin{gathered} loss=-\frac{1}{n}\sum _i^n{y}_i\log (\mathbb{P}[{\hat{y}}_i=1])+(1-y_i)\log (1-\mathbb{P}[{\hat{y}}_i=1]) \\ loss=-\frac{1}{n}\sum _i^n{y}_i\log (p_i)+(1-y_i)\log (1-p_i) \end{gathered}$$

可以发现，对于单个样本$i$，如果真实标签$y_i=1$，其 $loss=-\log (\mathbb{P}[{\hat{y}}_i=1])$随$\mathbb{P}[{\hat{y}}_i=1]$增大而减小；如果真实标签$y_i=0$，其 $loss=-\log (1-\mathbb{P}[{\hat{y}}_i=1])$随$\mathbb{P}[{\hat{y}}_i=0]$增大而减小。

有时将$p_i=\mathbb{P}[{\hat{y}}_i=1]$记为${\hat{y}}_i$，则变为
$$loss=-\frac{1}{n}\sum _i^n{y}_i\log ({\hat{y}}_i)+(1-y_i)\log (1-{\hat{y}}_i)$$

交叉熵损失

信息熵的定义为
$$H(X)=-\sum _{x\in \mathcal{X}}p(x)\log p(x)$$
现在再来看交叉熵的公式，它表示分布在共同空间$\mathcal{X}$的两个概率分布$p,q$之间的差异
$$H(p,q)=-\sum _{x\in \mathcal{X}}p(x)logq(x)$$
我们想借用交叉熵的概念，来衡量真实数据标签分布$y_1,y_2,...,y_n$和预测的标签分布${\hat{y}}_i,{\hat{y}}_2,...,{\hat{y}}_n$之间的差异，并把它称为交叉熵损失。注意它们要么都是连续分布，要不都是离散分布，考虑到真实数据标签是离散分布，即每个$y_i$要么等于1的概率为1，要么等于0的概率为1，故预测数据标签也应该是离散分布，即每个${\hat{y}}_i$等于1、等于0的概率都在0到1之间，即这里共同的空间$\mathcal{Y}=\{0,1\}$

举例如下表:

真实标签$y_i\in \mathcal{Y}=\{0,1\}$	$y_1$	$y_2$	$y_3$
$\mathbb{P}[y_i=1]$	1	1	0
$\mathbb{P}[y_i=0]$	0	0	1

预测标签${\hat{y}}_i\in \mathcal{Y}=\{0,1\}$	$y_1$	$y_2$	$y_3$
$\mathbb{P}[{\hat{y}}_i=1]$	0.7	0.9	0.2
$\mathbb{P}[{\hat{y}}_i=0]$	0.3	0.1	0.8

则在这个空间下每个样本的两个分布$p(y_i),q({\hat{y}}_i)$的交叉熵为
$$\begin{gathered} H(p(y_i),q({\hat{y}}_i))=-\sum _{y_i,{\hat{y}}_i\in \mathcal{Y}}p(y_i)log(q({\hat{y}}_i))=-\sum _{y_i,{\hat{y}}_i\in \{0,1\}}p(y_i)log(q({\hat{y}}_i)) \\ =-\mathbb{P}[y_i=1]\log (\mathbb{P}[{\hat{y}}_i=1])-\mathbb{P}[y_i=0]\log (\mathbb{P}[{\hat{y}}_i=0]) \\ =\{\begin{array}{ll}-\log (\mathbb{P}[{\hat{y}}_i=1])=-\log p_i,& \text{if yi=1 }\\ -\log (\mathbb{P}[{\hat{y}}_i=0])=-\log (1-p_i),& \text{if yi=0 }\end{array} \end{gathered}$$

则整体样本的交叉熵为
$$H=-\sum _i^n{y}_i\log p_i+(1-y_i)\log (1-p_i)$$
加上除以样本数
$$loss=-\frac{1}{n}\sum _i^n{y}_i\log (p_i)+(1-y_i)\log (1-p_i)$$
至此，我们发现二分类问题从MLE推出的损失函数，和交叉熵是一样的，这种损失函数我们称之为交叉熵损失函数。

1.2 多分类的交叉熵损失函数

举例如下表:

真实标签$y_i\in \mathcal{Y}=\{1,2,3\}$	$y_1$	$y_2$	$y_3$
$\mathbb{P}[y_i=1]$	1	0	0
$\mathbb{P}[y_i=2]$	0	0	1
$\mathbb{P}[y_i=3]$	0	1	0

预测标签${\hat{y}}_i\in \mathcal{Y}=\{1,2,3\}$	$y_1$	$y_2$	$y_3$
$\mathbb{P}[{\hat{y}}_i=1]$	0.7	0	0.1
$\mathbb{P}[{\hat{y}}_i=2]$	0.1	0.1	0.8
$\mathbb{P}[{\hat{y}}_i=3]$	0.2	0.9	0.1

• 从交叉熵来看，若共$C$个类别

$$\begin{gathered} H(p(y_i),q({\hat{y}}_i))=-\sum _{y_i,{\hat{y}}_i\in \{1,2,...,C\}}p(y_i)log(q({\hat{y}}_i)) \\ =-\mathbb{P}[y_i=1]\log (\mathbb{P}[{\hat{y}}_i=1])-\mathbb{P}[y_i=2]\log (\mathbb{P}[{\hat{y}}_i=2])-\cdots -\mathbb{P}[y_i=C]\log (\mathbb{P}[{\hat{y}}_i=C]) \end{gathered}$$
故可以推导出交叉熵损失为
$$\begin{gathered} \Rightarrow loss=-\frac{1}{n}\sum _{i}H(p(y_i),q({\hat{y}}_i)) \\ =-\frac{1}{n}\sum _i^n\sum _{k=1}^{C}1(y_i=k)\log \mathbb{P}[{\hat{y}}_i=k] \end{gathered}$$

• 从MLE看同样可以得到类似的结果

现在是多分类不再是伯努利分布，而是多项式分布(Multinomial distribution，投骰子问题) $y_i\sim P(p_i^1,p_i^2,...,p_i^C)$，这里$y_i$表示one-hot的一种情况$[y_i^1,y_i^2,...,y_i^C]=[0,0,...,1,...,0]$，即$y_i^k=1$时表示为第$k$类，预测值为$[{\hat{y}}_i^1,{\hat{y}}_i^2,...,{\hat{y}}_i^C]=[0.1,0.2,...,0.7,...,0]$。其实二分类也可以表示成这种形式，$[y_i^1,y_i^2]=[0,1],[{\hat{y}}_i^1,{\hat{y}}_i^2]=[0.1,0.9]$

对二分类的稍作变换
$$\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{m}\mathrm{a}\mathrm{x}\prod _i{p}_i^{y_i}(1-p_i{)}^{1-y_i}=\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{m}\mathrm{a}\mathrm{x}\prod _i{p}_i^{1\{y_i=1\}}(1-p_i{)}^{1\{y_i=0\}}$$
得到多分类
$$\begin{gathered} \Rightarrow \\ \mathrm{a}\mathrm{r}\mathrm{g}\mathrm{m}\mathrm{a}\mathrm{x}\prod _i(p_i^1{)}^{1\{y_i=1\}}(p_i^2{)}^{1\{y_i=2\}}\cdots (p_i^C{)}^{1\{y_i=C\}}=\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{m}\mathrm{a}\mathrm{x}\prod _i^n\prod _k^C(p_i^k{)}^{1\{y_i=k\}} \\ \Rightarrow \\ \log \mathcal{L}=\log \prod _i^n\prod _k^C(p_i^k{)}^{1\{y_i=k\}}=\sum _i^n\log \prod _k^C(p_i^k{)}^{1\{y_i=k\}}=\sum _i^n\sum _k^{C}1\{y_i=k\}\log (p_i^k) \end{gathered}$$
故可以推导出损失为和前面交叉熵导出的相同
$$loss=-\frac{1}{n}\sum _i^n\sum _k^{C}1\{y_i=k\}\log (p_i^k)=-\frac{1}{n}\sum _i^n\sum _k^{C}1\{y_i=k\}\log \mathbb{P}[{\hat{y}}_i=k]$$

1.3 比较

	二分类	多分类
MLE形式argmax	$\underset{p_1,p_2,...,p_n}{\mathrm{argmax}}{\prod }_i{p}_i^{y_i}(1-p_i{)}^{1-y_i}$	$\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{m}\mathrm{a}\mathrm{x}{\prod }_i(p_i^1{)}^{1\{y_i=1\}}(p_i^2{)}^{1\{y_i=2\}}\cdots (p_i^C{)}^{1\{y_i=C\}}$
单个样本交叉熵表达式	$H(p(y_i),q({\hat{y}}_i)=-{\sum }_{y_i,{\hat{y}}_i\in \{0,1\}}p(y_i)log(q({\hat{y}}_i))$	$H(p(y_i),q({\hat{y}}_i))=-{\sum }_{y_i,{\hat{y}}_i\in \{1,2,...,C\}}p(y_i)log(q({\hat{y}}_i))$
交叉熵损失	$-\frac{1}{n}\sum _i^n{y}_i\log (\mathbb{P}[{\hat{y}}_i=1])+(1-y_i)\log (\mathbb{P}[{\hat{y}}_i=0])$	$-\frac{1}{n}\sum _i^n\sum _k^{C}1\{y_i=k\}\log \mathbb{P}[{\hat{y}}_i=k]$

2. Hinge loss 铰链损失

Ref：
https://blog.csdn.net/hustqb/article/details/78347713
wiki

在机器学习中，hinge loss作为一个损失函数(loss function)，通常被用于最大间隔算法(maximum-margin)，而最大间隔算法又是SVM(支持向量机support vector machines)用到的重要算法(注意：SVM的学习算法有两种解释：1. 间隔最大化与拉格朗日对偶；2. Hinge Loss)。

Hinge loss专用于二分类问题，标签值$y=\pm 1$，预测值$\hat{y}=wx+b\in \mathbb{R}$.

对任意一个样本，hinge loss定义为
$$\mathcal{L}({\mathbf{x}}_i,y_i)=\max \{0,1-y_i\cdot {\hat{y}}_i\}=\max \{0,1-y_i(\mathbf{w}{\mathbf{x}}_i+b)\}$$
注意这里的${\hat{y}}_i=\mathbf{w}{\mathbf{x}}_i+b$是没有经过sign等激活函数的，是直接在数据平面上经过变换后的值。可以取任意值。

${\hat{y}}_i=\mathbf{w}{\mathbf{x}}_i+b>0$表示一类，${\hat{y}}_i=\mathbf{w}{\mathbf{x}}_i+b<0$表示另一类。

当$y_i\cdot {\hat{y}}_i>1$时，$\mathcal{L}({\mathbf{x}}_i,y_i)=0$;

当$y_i\cdot {\hat{y}}_i<1$时，$\mathcal{L}({\mathbf{x}}_i,y_i)=1-y_i\cdot {\hat{y}}_i=1-y_i\cdot (\mathbf{w}{\mathbf{x}}_i+b)$.

对比感知机的loss为：

当$y_i(\mathbf{w}{\mathbf{x}}_i+b)>0$时，$\mathcal{L}({\mathbf{x}}_i,y_i)=0$;

当$y_i(\mathbf{w}{\mathbf{x}}_i+b)<0$时，$\mathcal{L}({\mathbf{x}}_i,y_i)=-y_i\cdot (\mathbf{w}{\mathbf{x}}_i+b)$.

如下图：

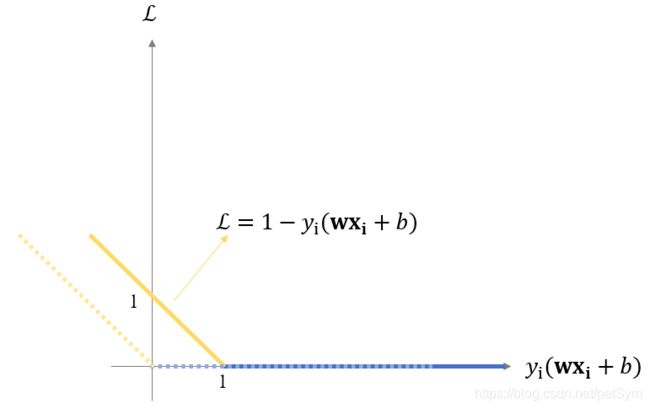
hinge loss相对于感知机的loss向右平移了一个单位，相当于不再单单要求分类正确，还对每个点离分类平面的距离有一定的要求。这其实就是SVM中，从最优化求几何间隔最大的分离超平面，到最优化函数间隔最大的分离超平面，再到约定的函数间隔的值对优化求解超平面没有影响，优化问题是等价的，故而直接取了函数间隔为1，得到约束条件
$$\begin{gathered} y_i(\mathbf{w}{\mathbf{x}}_i+b)\ge 1 \\ \Rightarrow \\ {y}_i(\mathbf{w}{\mathbf{x}}_i+b)-1\ge 0 \end{gathered}$$
即满足以上远离超平面一定距离的条件，才认为分类是正确的。这就得到了我们的hinge loss中，满足条件的时候，分类损失为0。可以看到，它比感知机的要求更进一步、更严格。