深度学习入门笔记之ShuffleNet
目录
- ShuffleNet V1
-
- ShuffleNet V1的亮点
- ShuffleNet V2
-
- 对于网络复杂度的考虑
- 高效网络设计实用指南
-
- 输入输出具有相同channel的时候，内存消耗是最小的（相同维度的通道数将最小化MAC）
- 过多的分组卷积操作会增大MAC，从而使模型速度变慢
- 模型中的分支数量越少，模型速度越快
- 不要忽略元素级操作
- V1有何不好？
- ShuffleNet V2结构
- ShuffleNet V2网络结构
- ShuffleNetV2的分析
- ShuffleNetV2的结果对比
论文名：ShuffleNet: An Extremely Efficient Convolutional Neural Network for Mobile Devices
论文地址：https://arxiv.org/abs/1707.01083v1
CVPR：2017
论文名：ShuffleNet V2: Practical Guidelines for Efficient CNN Architecture Design
论文地址：https://arxiv.org/abs/1807.11164
会议：ECCV2018
ShuffleNet V1
ShuffleNet V1的亮点
Group Convolution
这算是整个ShuffleNet的优化核心，Group Convolution操作早在AlexNet的时候就被拿来进行速度的优化了，其运算的过程可以参考这里，简单的说就是对一个输入通道为N的特征图进行的卷积操作拆分为对g个通道为N/g的特征图进行卷积，这样的方法在速度和参数上都会有大幅的提升。下表以卷积核为 D K × D K D_{K} × D_{K} DK×DK ，特征图大小为 D F × D F D_{F} × D_{F} DF×DF，输入通道数为N，输出通道数为M，简单的说明一下速度和参数的提升：
| No Group | With Group | |
|---|---|---|
| Parameter | N × M × D K × D K N ×M ×D_{K} × D_{K} N×M×DK×DK | N / g × M / g × D K × D K × g N /g×M/g ×D_{K} × D_{K}×g N/g×M/g×DK×DK×g |
| Computation | D F × D F × N × M × D K × D K D_{F} × D_{F}×N ×M ×D_{K} × D_{K} DF×DF×N×M×DK×DK | D F × D F × N / g × M / g × D K × D K × g D_{F} × D_{F}×N /g×M/g ×D_{K} × D_{K}×g DF×DF×N/g×M/g×DK×DK×g |
可以看到两个参数均缩小g倍，也就是说当group number越大，优化的越好（但是在ShuffleNetV2中作者论证出group number对于网络的速度来讲并不是越大越好，g=1是对速度最友好的）。
Channel Shuffle
对于上述的Group Convolution，很容易想到一个问题就是在卷积的时候，仅仅是将这一个Group的特征图进行了融合，但是不同的组别之间缺没有充分的连接，长此以往，不同的特征图对于对方的了解就越来越少，虽然网络的全连接层会帮助不同特征图相互连接，但是可以预想的是这样的连接融合的次数较少，不如不分组的情况。
基于上述的情况，作者提出把每个组的特征图分为一定组在每一层都进行一定程度的乱序结合，以这样的方式增加特征图的连接融合次数，过程如下图所示：
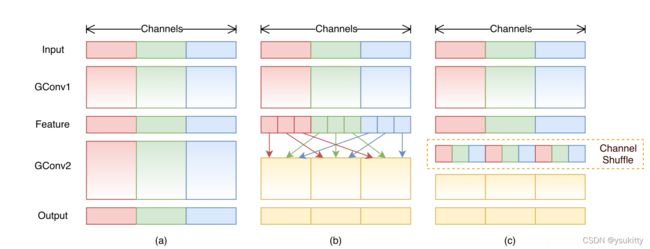
ShuffleNet unit
整个单元其实比较好理解，直接上图如下：
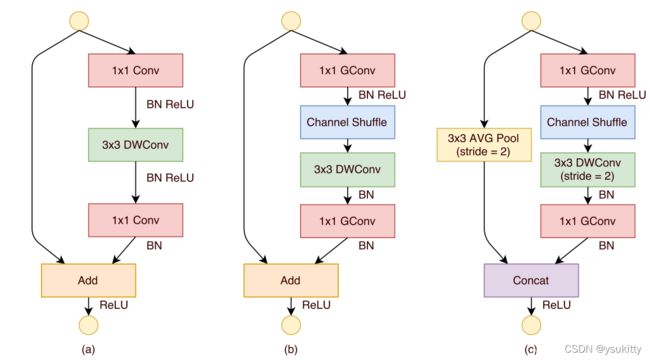
图（a）是使用DWconv的bottleneck操作；图（b）是使用添加了Channel Shuffle之后的单元模型（该单元模型并不进行图像大小的调整），Channel Shuffle操作在1×1的卷积操作之后，也就是先对通道进行了收缩，随后进行通道调整，最后卷积在调整回原来的通道数；图（c）是使用该单元进行池化的操作，值得注意的是经过该单元之后，通道数为原先的2倍。
作者也说道，对于ResNet的bottleneck操作，一共需要的操作为 h w ( 2 c m + 9 m 2 ) h w ( 2 c m + 9 m^2) hw(2cm+9m2)，其中 h w hw hw为图像的宽度和高度， c m cm cm为输入通道数和收缩到的通道数，卷积核默认为 3 × 3 3×3 3×3，而本文的shuffleNet单元的整体操作花费为 h w ( 2 c m / g + 9 m ) hw(2 c m /g + 9 m) hw(2cm/g+9m)，其中 m 2 − > m m^2−>m m2−>m得益于采用了DWConv，而GConv的贡献主要在于两端的1×1卷积操作。
ShuffleNet Architecture和实验
（1）ShuffleNet的网络结构如下图所示：
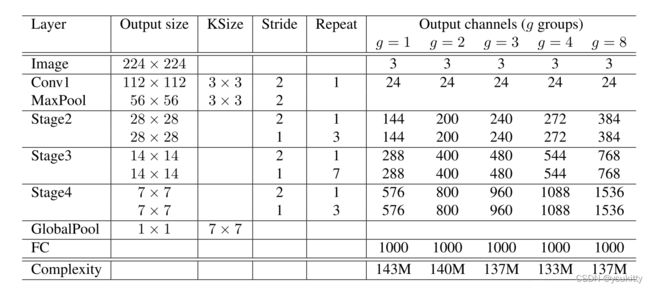
（2）可以看到，随着分组的增加，最终的复杂度（论文中以FLOPS作为衡量标准）相应的减少，这和我们对于Group Convolution操作的期望相同；随之而来的一个问题是，**采用了这样的方式会对准确率有影响吗？**出人意料的，该改进也比传统的网络优秀一些。
（3）除了标准网络，作者也按照MobileNetV1的思路，对于网络设置了一些超参数s，表示通道数的多少，例如s=1，即标准的网络结构，通道数如上图所示；s=0.5表明每个stage的输出和输入通道数都为上图中通道数的一半，其他的类似。通过通道缩放s倍，整个计算复杂度和参数均下降 s 2 s^2 s2倍。下表是作者的一些实验数据。
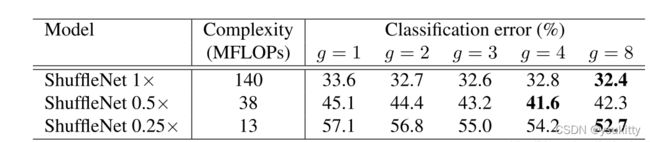
上表中有一个很有意思的现象，就是在s=0.5的时候，较大的group参数居然导致准确率的下降，而s=0.25的时候，较大的group参数使得准确率提高；这里作者也仅仅是一笔带过，只是说当每一组的特征图数变少，可能影响网络的表征能力。
（4）Shuffle操作有无的对比
作者也对比了网络添加shuffle和不添加shuffle的区别，如下图
可以看到，网络添加了shuffle操作之后准确率确实有了一部分的提升。
（5）与MobileNet的对比
下图是ShuffleNet与MobileNet的对比，可以看到精确度上提高不少。
ShuffleNet V2
如MobileNetV2一样，ShuffleNetV2也是对深度神经网络的深层探讨，但是不一样的地方在于，ShuffleNetV2的优化点更精细一些，完全瞄准轻量化这个目标而设计。
对于网络复杂度的考虑
**作者上来就提出了一个被大家广泛忽略的一个问题：我们广泛使用的FLOPs真的可以很好的反应我们网络的复杂度吗？**显然答案是否定的，作者举出的例子是MobileNetV2的FLOPs和NASNET-A是相当的，但是速度却快出了后者很多。下图是更多的作证。
图c是经典小网络在GPU上的MFLOPs与速度（Batches/sec）的关系。 图d是经典小网络在ARM上的MFLOPs与速度（Batches/sec）的关系。
我们可以发现，具有相似的FLOPs的网络，执行的速度却不一样。有的相差还挺大。
**作者在此提出了第一个观点：因此，使用FLOP作为计算复杂度的唯一指标是不充分的。**理由：
- FLOPs没有考虑几个对速度有相当大影响的重要因素：MAC和并行度
MAC(内存访问成本)，计算机在进行计算时候要加载到缓存中，然后再计算，这个加载过程是需要时间的。其中，分组卷积（group convolution）是对MAC消耗比较多的操作。
并行度，在相同的FLOPs下，具有高并行度的模型可能比具有低并行度的另一个模型快得多。如果网络的并行度较高，那么速度就会有显著的提升。
2）计算平台的不同
不同的运行平台，得到的FLOPs也不相同。有的平台会对操作进行优化，比如：cudnn加强了对3×3conv计算的优化。这样一来，不同平台的FLOPs大小确实没有什么说服力。
针对以上的发现，作者提出直接的对网络速度测量应该代替FLOPs;要在目标计算平台上计算，不然结果不具有代表性；并针对网络的速度提出了四点指导建议。
高效网络设计实用指南
分析对比两个具有代表性的最先进网络的运行时性能（ShuffleNetV1，MobileNetV2）。
分别在GPU和CPU上去对ShuffleNetV1，MobileNetV2的运行时间进行了测试。
GPU使用单个NVIDIA GeForce GTX 1080Ti。卷积库是CUDNN 7.0。
CPU使用高通骁龙 810。
测试结果如下：
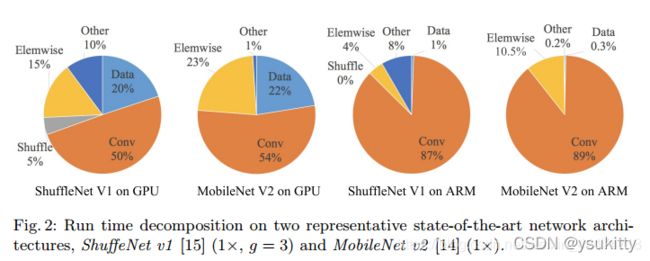可以看到，整个运行时被分解用于不同的操作。处理器在运算的时候，不光只是进行卷积运算，也在进行其他的运算，特别是在GPU上，卷积运算只占了运算时间的一半左右。
我们将卷积部分认为是FLOPs操作。虽然这部分消耗的时间最多，但其他操作包括数据IO，数据混洗和逐元素操作（AddTensor，ReLU等）也占用了相当多的时间。因此，再次确认了模型使用FLOPs指标对实际运行时间的估计不够准确。
基于这一观察，作者从几个不同的方面对运行时间（或速度）进行了详细分析，并为高效的网络架构设计提出了几个实用指南。
推出了四个高效网络设计指南，这些指南不仅仅考虑了FLOP。
输入输出具有相同channel的时候，内存消耗是最小的（相同维度的通道数将最小化MAC）
作者为了验证卷积层两端的通道数对于速度的影响，自己搭建了一个验证网络，参数如上表所示，可以看到当两端的通道数之比为1:1的时候，模型的速度是最快的（不同比例的通道数不一致主要是为了保证FLOPs是相同的）。
过多的分组卷积操作会增大MAC，从而使模型速度变慢
之前有提到，分组卷积操作会减少参数，这样一来网络的计算量也就减少了。但是呢，认为网络的计算量减少，不代表模型的速度也会减少。MAC主要的消耗来源就来自分组卷积，分组卷积一多，MAC消耗的越多，模型速度也就变慢了。
很清楚的看到，g越小，速度越快。因此，作者建议应根据目标平台和任务仔细选择组号。虽然组卷积能增加模型的准确度，但是作者认为盲目使用较大的组号是不明智的，因为这将会使得计算成本增加带来的缺点大于准确度增加带来的优点。
模型中的分支数量越少，模型速度越快
作者这里使用自己搭建了一些网络进行验证，网络的结构如下（这里作者似乎并没有保证FLOPs是一样的）：
最终的结果如下所示：
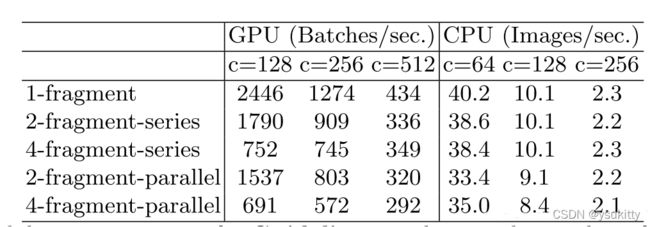
其中， 2-fragment-series表示一个block中有2个卷积层串行，也就是简单的叠加； 4-fragment-parallel表示一个block中有4个卷积层并行，类似Inception的整体设计。 可以看出在相同FLOPs的情况下，单卷积层（1-fragment）的速度最快。
不要忽略元素级操作
Element-wise包括Add/Relu/short-cut/depthwise convolution等操作。元素操作类型操作虽然FLOPs非常低，但是带来的时间消耗还是非常明显的，尤其是在GPU上。元素操作虽然基本上不增加FLOPs，但是所带来的时间消耗占比却不可忽视。也即Small FLOPs heavy MAC。
作者为了验证这个想法，对bottleneck这个层级进行了相应的修改，测试了是否含有Relu和short-cut两种操作的情况，对比如下：
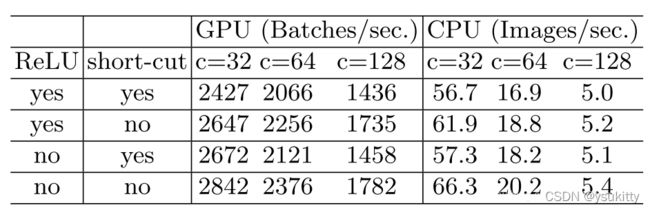
结论一目了然，没有两种操作的时候，更快一些。而且一个有意思的现象是，去掉short-cut对于速度的提升比Relu快一些，可以想到的是Relu只是对一个tensor进行操作，而short-cut是对两个tensor进行的操作。
结论（作者首先简要总结了一下4个guideline）
1）. 使用“平衡的”的卷积层（输入输出通道相同）；
2）. 小心使用分组卷积；
3）. 减少使用碎片化的操作；
4）. 减少元素级的操作；
随后作者分析了最近的一些比较火的网络结构：
ShuffleNetV1违反了G2，bottleneck的结构违反了G1，而MobileNetV2使用的inverse bottleneck的结构违反了G1，其中夹杂的DWconv和Relu都违反了G4，自动生成结构（auto-generated structures）高度碎片化违反了G3。
V1有何不好？
如上一节的结论所述，逐点组卷积增加了MAC违背了G2。这个成本不可忽视，特别是对于轻量级模型。另外，使用太多分组也违背了 G3。
瓶颈结构违背了G1与多单位违背了G3。
ShuffleNet V2结构
为了实现较高的模型容量和效率，关键问题是如何保持大量且同样宽的通道，既没有密集卷积也没有太多的分组Add操作是元素级加法操作也不可取违反了G4。因此，为了实现较高的模型容量和效率，关键问题是如何保持大量且同样宽的通道，既没有密集卷积也没有太多的分组。
Channel Split操作
上图中（a）（b）是ShuffleNet V1的层结构，而后面的（c）（d）是ShuffleNet V2的层结构。
结构特点：
1.在每个单元的开始，通过Channel split将c特征通道的输入被分为两支，分别带有 c−c’ 和c’个通道。按照准则G3，一个分支的结构仍然保持不变。另一个分支由三个卷积组成， 为满足G1，令输入和输出通道相同。与 ShuffleNet V1 不同的是，两个 1×1 卷积不再是组卷积(GConv)，因为Channel Split分割操作已经产生了两个组。
2. 这样分开之后，一组是通过short-cut通道，一组经过bottleneck层的输入输出的通道数就可以保持一致（G1）；卷积之后，把两个分支拼接(Concat)起来，从而通道数量保持不变 (G1)，而且也没有Add操作（element-wise操作）（G4）。然后进行与ShuffleNetV1相同的Channel Shuffle操作来保证两个分支间能进行信息交流。
可以看到，这样一个简单的通道分离的操作带来了诸多好处；但是从理论上来说，这样的结构是否还符合short-cut的初衷（即bottleneck学到的是残差Residual部分）？这里笔者也不好妄加揣测，但是可以想到的是经过后面的Channel Shuffle的乱序之后，每个通道应该都会经过一次bottleneck结构。
上述的结构是不改变输入输出通道数和特征图大小的情况，而池化操作使用图（d）代替了，跟ShuffleNetV1类似，经过这样的结构之后，图像通道数扩张为原先的2倍。
ShuffleNet V2网络结构
相似于ShuffleNetV1，网络也使用了4个不同的stage，结构如下图：
值得特别注意的是！channel数都异常的小！这里作者并没有特别的解释这个现象（按照MobileNetV2中对于Relu的分析，这个地方似乎有点儿激进?）。
ShuffleNetV2的分析
作者得到的结果是ShuffleNetV2既高效而且准确，主要分析有两点原因：
1）. 每个结构层（building block）的高效率使得能够使用更多的特征通道和更大的网络容量（这个地方并没有很理解）；
2）. 在每个结构层，都有一部分的通道直接通道下一个结构层，提高了特征的重用度；
论文有对比了DenseNet和ShuffleNetV2重用度的区别，如下图：
可以看到，在特征重用方面，ShuffleNetV2在不同层之间保持了连接，但是不像DenseNet，过远的层之间也会有很大的连接。
ShuffleNetV2的结果对比
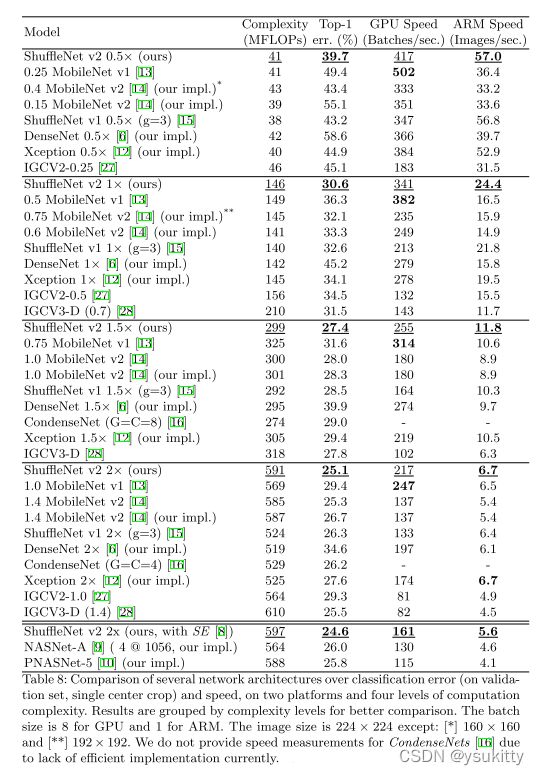
上述结果中有一个现象是MobileNetV1的速度在GPU上是最快的，作者说明这个现象是因为MobileNetV1比于之后的几个轻量级网络，具有更贴近的4个guide line的设计，因此在GPU的速度更快，但是我们看到，在CPU上，ShuffleNet又扳回一城，而且快了许多。
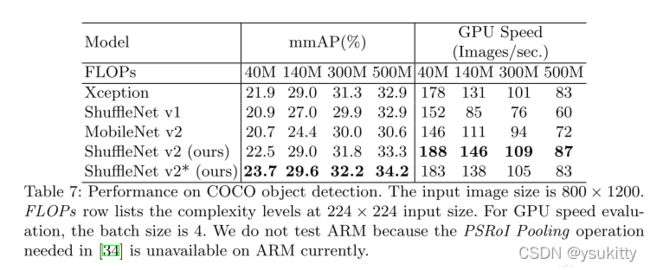
这个图中带*号的模型是作者从Xception中得到了一些启发，表明更大的感受野对于detection的任务更友好，因此作者在每个结构的1×1卷积之前添加了一个3×3的DWconv卷积层增大感受野，结果确实有所提升。
参考资料：
轻量级神经网络：ShuffleNetV1到ShuffleNetV2
ShuffleNet V1/V2整理阅读