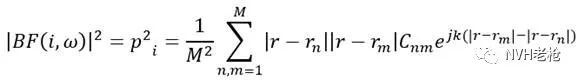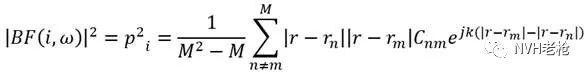麦克风声源定位原理_声源定位—如何定位到噪声根源？

前言

TPA(传递路径分析)专题系列已经开篇。其遵循方法论：

源(Source)——路径(Path)——响应(Receiver)

有人说TPA好，它可以识别出路径处甚至源的载荷特征，可以量化各个路径的贡献量。

有人说声源定位好，不管东西南北中，“源”自其中。

但是，声源定位识别出来色彩丰富的一个结果，这结果被您拿来应付工作了，还是真正帮您解决了问题？声源定位定位到了噪声的根源了么？对于一些声源现，而源(根源)不见(照不到)的结构，该怎么使用声源定位系统？

接下来我们计划更新一系列文章对声源定位软硬件系统进行详细介绍，介绍内容大致包括：Beamforming波束形成技术，Deconvolution反卷积技术，声全息技术，二维和三维阵列硬件技术综述。

(一)Beamforming波束形成本质

Beamforming基本原理：

波束形成采用延时求和算法，时域和频域均可实现，其基本理论非常简单易懂。以下假设理想情况下的简化模型，通过麦克风传声器采集的原始时域信号，采用加减乘除四则运算带您走进Beamforming波束形成的世界。

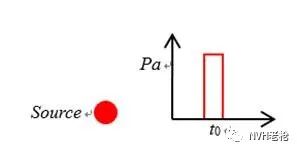
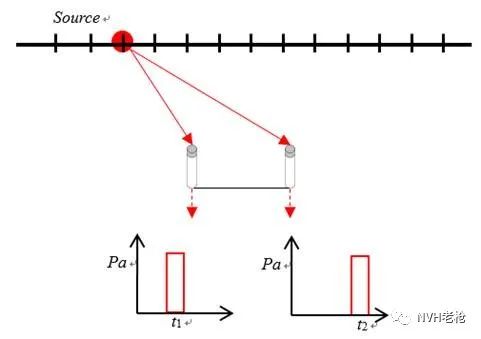
假设声源发出一个具有一定宽度的理想脉冲点声源，在t₀时刻发声，如下图所示：

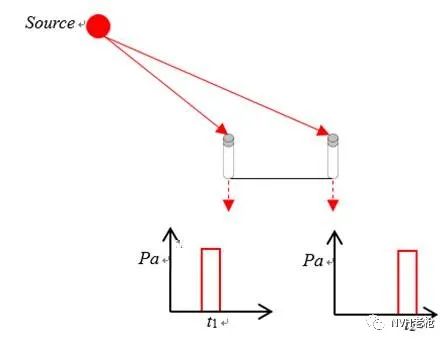
假设阵列只包含2个理想的麦克风传声器位于阵列上的不同坐标点，同步采集前提下(不考虑离散采样等因素)，信号如下所示：

理想情况下(不考虑距离衰减等因素)，两个麦克风采集到相同信号的时刻是不同的。如上图所示，声源在某一时刻发出的信号，左侧麦克风先于右侧采集到该信号。

补充知识：加法和除法的正确应用。

对多个麦克风采集到的原始时域数据做平均严谨科学么？且看分解：

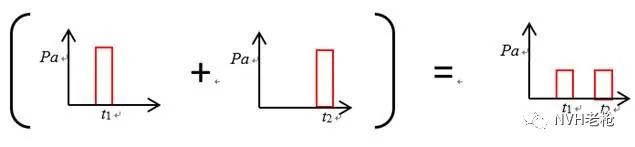
如下图所示,将上面两个麦克风采集到信号相加除以2，得到一个“平均”信号。Oh, No! 这不是我要的那种结果~，结果~~~

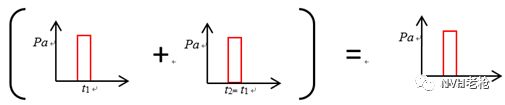
但是将两个麦克风采集到的信号对齐了再平均会怎么样呢？Oh, yeah!

怎么对齐？若声源到两个麦克风的距离已知，声速已知，那么~~~

言归正传：正确的加法和除法在Beamforming中的应用。

实际情况下，声源位置是未知的，因此需要计算所有网格点。假设计算的网格点分布在一条与点声源相交且平行于两个麦克风连线的直线上。如下图所示：

假设每个网格点都有声源，对上面的两个麦克风采集到的信号分别按照每个网格点的距离进行“对齐”求和再平均(延时求和再平均)。那么网格点上的声压分布示意图如下(网格点间进行简单插值)：

注：示意图(并未考虑周期性旁瓣等等因素的影响)，若追求严谨，请看后续程序计算的真实结果。

小伙伴们，有没有惊讶的发现，真实声源位置的声压要大一些？有没有发现，原来Beamforming 这么简单粗暴？原来我们被Beamforming这个词蒙蔽了这么多年！！！

但是，Beamforming基本原理虽然简单粗暴，但是真正做好Beamforming技术也不是一件容易的事儿。接下来，我们来一起看看不同的Beamforming技术。

(一)Beamforming波束形成分类

以下将概述Beamforming的不同分类。世间分类千百种，我只取我懂的几种~~~。笔者将用自编的程序结合商业软件对比来阐述各种Beamforming的优势和劣势。

按照频谱数据类型分类：

包括基于自谱，互谱，去除对角线元素的互谱(还有一些PCA等等就不一一概述)。根据数字信号分析与处理的理论，信号在时域中的延时τ相当于频域的相移ωτ，因此这里就不再重复介绍频域的基本理论了。也有许多文章喜欢用矩阵和转向列向量的形式类表述下述公式，但是本质都是相同的。

基于自谱：

基于自谱的Beamforming波束形成公式如下(注：声压幅值采用不同的归一化方或者不同频率采用不同的计权系数，公式会有细微差别，但本质相同)：公式落掉，下期补上

BF(i,ω)为第i个网格点，频率为ω的Beamforming输出结果(声压); 为第i个网格点与第m个麦克风的距离; 为第m个麦克风的频谱信号，=，c为声速；k为波束。

下图为阵列，识别网格面，第m个麦克风与第i个识别网格点的几何关系。

补充探讨：声压幅值采用不同的系数(本公式采用每个网格点到各个麦克风的距离作为系数，实际上是将Beamforming输出的声压结果归一化到距识别表面1m远处的位置)和不同频率点的加权系数，得到云图的幅值，动态范围和空间分辨率是不同的。例如上述公式得到的云图幅值是归一化到1m处，幅值较为准确，但往往会损失一定的空间分辨率。

基于自谱的Beamforming波束形成算法优点是速度快，假设阵列有n个麦克风，那么计算量就是n个麦克风的自谱进行延时求和平均；缺点是每个麦克风，线缆，数采通道的本底噪声会影响声源定位系统的整体性能，对动态范围影响最为明显(动态范围本就不会太高的Beamforming算法，动态范围是很珍贵的！)。

基于互谱和去除对角线元素的互谱(CSM/CSMDR):

其实自谱公式将等式两侧进行平方(功率谱，本身乘以其共轭)，就得到的基于互谱的Beamforming公式。

该公式的各项含义与基于自谱的相同，唯一要注意的是为多个时间块平均的互谱。大家可能有疑问，为何？自谱不是挺好的，弄成互谱后，n个麦克风的阵列要用n x n条互谱进行延时求和，计算量陡增！且听我慢慢道来：

• 所谓两个信号的互谱，也就是信号1的频谱(幅值和相位)乘以信号2的频谱的共轭，因此互谱的幅值等于两个信号的幅值相乘，但是相位为两个信号的相位差。

• 麦克风，线缆，数采通道的本底噪声往往是互不相关(相关：同一频率具有相同的相位差)，用每个时间块计算上面噪声信号的互谱相位不是恒定的。

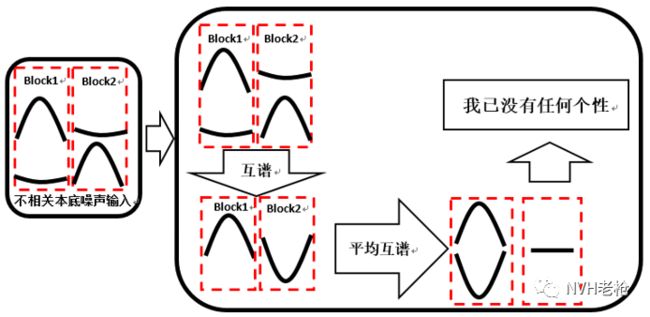
• 那么上面的本底噪声的互谱求平均后会怎样？如果想象不出来，且看下图(不够严谨，帮助大家理解)

自谱：两个背景噪声小伙伴相约，要去为声源定位做出自己的贡献~~~

互谱：另外两个不相关本底噪声决定先要变得更强大~~~，乾坤大挪移(多次合并)合二为一，先变成平均的互谱，结果~~~

由上可知，基于互谱的Beamforming能够消除不相关的本底噪声干扰，提高Beamforming算法的性能。

能否再进一步？答案是肯定的，我们将互谱矩阵的对角线(自谱)去掉，用剩下的互谱元素来计算Beamforming，公式如下：

以上尽量通过通俗易懂的描述和图形展示介绍了基于频谱类型的几种Beamforming方法的基本原理。

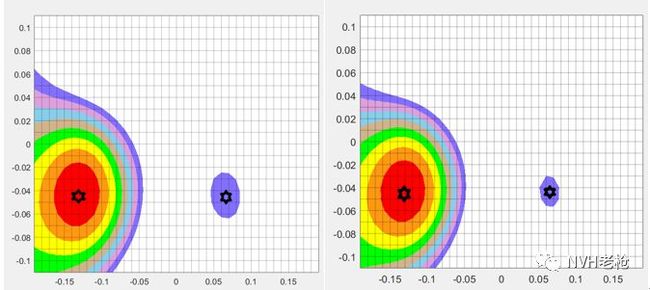
下面通过编程计算，分析同一组半消声室采集的数据，分别采用互谱矩阵和采用互谱矩阵去对角线元素的Beamforming算法的对比。首先对比8dB动态范围条件下，分别计算互谱和去掉对角线元素的互谱Bea forming结果。如下图所示，黑色标识处为两个量级不同的人工点声源：

互谱(左)与 去自谱互谱(右)识别结果对比(动态范围均为8 dB)

细心的您发现不同了么？是的，仅仅去掉对对角线元素后，空间分辨率就有了肉眼可见的提升，那么相比于采用自谱的波束形成就不再做对比了。

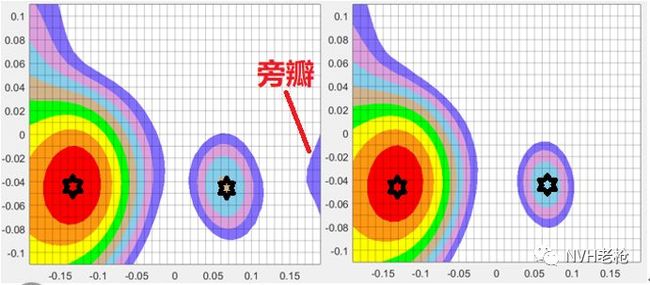
接下来我们将动态范围增大直到出现旁瓣，对两种方法的动态范围进行对比，如下图所示：

互谱(左)与 去自谱互谱(右)识别结果对比(动态范围均为 12 dB)

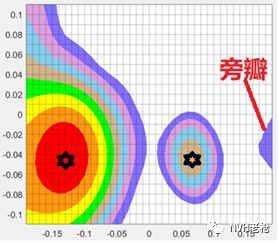
去自谱的互谱(动态范围均为 14.5 dB)

由上图可知，去除自谱的互谱波束形成算法对动态范围的提升显著。因此去对角线元素的互谱波束形成算使用广泛。

续：Beamforming的分类方法还很多。比如按照应用于二维阵列还是三维阵列(通常是球形)分类，包括2D-Beamforming，3D-Beamforming。按照是否利用反射面的反射信号(比如风洞驻室地面对声音的反射)，包括使用“虚拟麦克风阵列”(叫法不一)技术的Beamforming。按照如何对每个麦克风的声压信号的幅值和不同的频率进行计权，包括多种其他多种Beamforming技术。若知后续，请持续关注~~~

参考文献：

[1] Thomas F.Brooks. A Deconvolution approach for the mapping of acoustic sources[J],Journalof Sound and Vibration 294 (2006) 856–879

[2] T.F.Brooks, W.M. Humphreys Jr., Flap edge aeroacoustic measurements and predictions,Journal of Sound and Vibration 261 (2003)31–74.

[3] P.Sijtsma and H. Holthusen. Corrections for mirror sources in phased arrayprocessing[C],The 9th AIAA/CEAS Aeroacoustics Conference as AIAA Paper 2003-3308, HiltonHead, South0020 Carolina, USA, 12-14 May2003