陈键飞:基于随机量化的高效神经网络训练理论及算法
【专栏:前沿进展】随着预训练模型参数规模的增长,所需的算力也不断增加,从算法层面研究和处理模型规模的增长成为研究者关注的话题。近期举办的Big Model Meetup第二期活动,特邀清华大学助理教授陈键飞介绍随机量化的高效神经网络训练理论及算法。智源社区对报告进行了整理。
活动回看地址:
https://event.baai.ac.cn/activities/175
演讲人:陈键飞
整理人:李栋栋
审校:赵万铖、戴一鸣
01
背景
众所周知,当前大模型的参数量在不断增加,计算量也在增加,但是硬件并没有提供相应的增长速度。因此我们必须从算法的层面上出发、去研究,如何处理模型规模的继续增长。量化(Quantization)技术是有潜力的解决方法。
为何量化是一个很有效的手段?首先从计算的效率和吞吐量来看,以GPU为例,如果用Int4,也就是4位整数,它在GPU相对单精度的浮点数能提供快64倍的速度,所以若能降低神经网络的精度,对于计算是有很大帮助的。另外,量化对能耗和芯片的面积同样很有帮助。最后,在存储上,如果能把32位的权重压缩到1位的话,就能节省32倍的存储。对于现有一些大模型来说,将参数存储下来非常困难,而量化会对其有很大的帮助。
02
什么是量化
量化究竟指的是什么?本次报告中量化是指,首先有一个单精度矩阵X,想把它量化,就是把它分解成一个单精度的标量S_X乘上一整个矩阵,这个矩阵是一个量化过的、8位的整数。S_X表示原来X中的数值范围,整数矩阵用来存储真实的数据,这个转换的过程就是量化的过程,相反的过程称之为反量化的过程。仅用这两个操作就能实现存储空间的节省,量化后的整数矩阵存储起来比原先的浮点矩阵的更小。但是要计算加速的话,这样还不足够,还需考虑已经转换为这种格式的两个矩阵如何直接做乘法,而不是先反量化再做浮点数乘法。
考虑两个浮点矩阵的乘法,可以先把矩阵量化,转成分解的格式,然后分别对两个整数矩阵做乘法,这个操作是整数矩阵对整数矩阵的乘法,如果硬件支持高效的整数运算的话,就会得到一个很好的加速。从这个例子可以看到,加速计算要比节省存储困难,至少要有一个低精度矩阵乘法的算子,并且也需要硬件的支持。
03
量化方法概览
量化是一个比较广的领域,为解决不同的任务需求设计出的量化方法是不能互相替代,但这些方法又很容易混淆。总得来看,量化方法可以分成加速和压缩两大类。加速就是把计算做得更快一些,它又具体的分成推理阶段的加速和训练阶段的加速。
压缩只用前面提到的量化和反量化操作,不考虑做更快的矩阵乘法,不需要专门硬件去配合,但这样只能做到存储空间的节省。压缩有许多应用,比如压缩模型本身的大小,像1.7万亿参数的模型本身存储起来就非常大,若可以压缩就会降低存储开销。压缩的另一个应用是梯度压缩,比如超大规模的并行训练时,通信带宽受限,若能把带宽压缩到1位的话,对降低通信的开销会有很大的帮助。
今天我们主要从训练的加速、训练的内存节省来介绍量化所能做到的理论性能保证。量化是一个有损操作,该怎么样去分析一个使用了量化操作的训练算法?这种训练为什么是有道理的?
04
量化用于加速
首先看加速的例子,这里对比几种常见的场景,第一种是全精度训练(Full-Precision Training),在前向和反向的传播中,都用全精度操作,所以它是没有加速的。
另外一种场景是量化感知训练(Quantization-Aware Training),它是在前向传播阶段的每一层,将上一层的输入和这层的参数相乘,这是一个矩阵乘法操作,但是乘之前要做一个量化,把两个矩阵都转成低精度的,然后用低精度数去做运算,所以他的前向传播可以在低精度的硬件上进行计算,获得加速。但是反向传播的时候,需要全精度的去计算梯度,因此这个方法只适用于推理阶段的加速,训练阶段因为要算完整的反向传播所以训练速度不快。
更进一步,如果训练也想加速的话,梯度也要做量化。要在反向传播时,把每一层的梯度全部量化,把前向传播传到反向传播的信息也都量化,从而保证反向传播也是低精度的操作。这就是今天关注的例子,称为全量化训练(Fully-Quantized Training)。
全量化训练是一个近似算法,前向传播是近似的,反向传播梯度也是近似算的,这些近似到底会对训练的稳定性、收敛性产生什么样的影响?这是今天希望回答的问题。
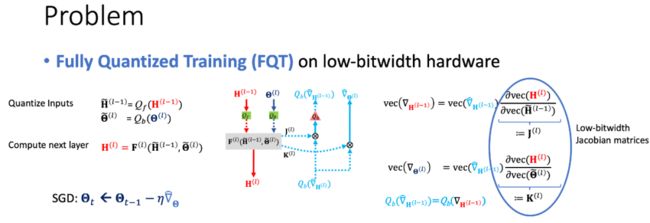
考虑全量化训练的数学表示:
前向传播的时候每一层的特征都要过一下量化器,然后把量化过的特征送进一个层里,这个层是一个任意的函数。反向传播的时候,根据链式法则可以把每层的梯度写成雅可比矩阵与上一层的梯度相乘的形式。
用这套近似的算法算出来的梯度去做梯度下降,因为每一层都会对梯度做量化,梯度的误差会不断的积累的,这是分析的难点。作为一个训练算法,我们想要知道:
算法是否能收敛?收敛性是对训练算法最基本的要求;
收敛速度有多快?如果量化算法比全精度算法收敛速度慢很多,需要更多的轮数的话,量化就没有意义了,得不偿失;
量化的数据格式如何影响收敛性?应该选择整数还是浮点数?几bit是足够的?
一般来说,当前向传播和反向传播都量化时,前向传播相对做得比较好,用比较少的bit就可以做到较好的效果,反向传播是瓶颈。所以本次报告只研究梯度量化(反向传播)对算法的影响,即把全量化训练和量化感知训练作对比。
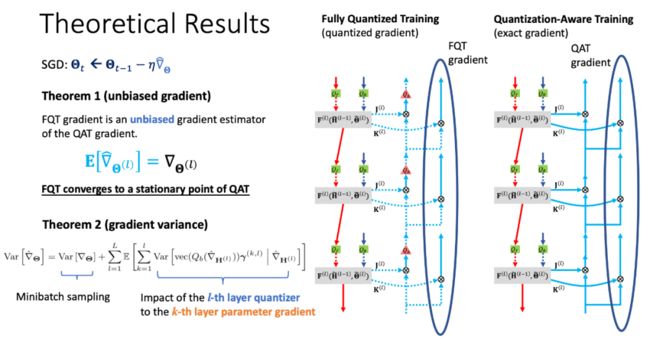
之前已经讲到,量化感知训练前向传播是量化的,反向传播没有量化。量化感知训练和全量化训练都是训练同一个模型的随机梯度下降算法,只是它们用的梯度不同,量化感知训练用的是“精确”的梯度,是一个“真实”的下降方向,而全量化训练用的是近似的梯度,在计算梯度的过程中引入了量化。只要比较这两个梯度,就可以知道两个算法的表现有何差异。
实际上量化感知训练采取了straight-through estimator(STE)估计梯度,这个梯度也不是精确的。但是实践中,利用STE的量化感知训练已经表现足够好了,所以我们只想分析额外引入的梯度量化造成的影响。
此时需要用到一个关键的假设,即反向传播里面的梯度的量化都是无偏的随机操作。比如把0.7这个数字量化成整数,可以有70%的概率变成1,30%的概率变成0。这样虽然输出的是整数,但是它的期望仍然是0.7,是无偏的。因为反向传播的每步都是线性操作(雅克比矩阵乘梯度向量),即使在每层计算梯度的时候都引入了无偏的量化噪声,量化误差也逐层累积,但最终的梯度仍然是无偏的。
无偏的梯度是很好的,因为现在做的是随机梯度下降,而随机梯度下降只要梯度是无偏的,那么取足够小的学习率,训练足够长的时间,最终还是可以收敛的,这保证了算法的收敛性。
进一步的,算法收敛得多快,就取决于随机量化带来的方差有多大了。分析梯度的方差,可以具体把方差拆成两项的和,第一项是由于Sampling Minibatch带来的,这是因为随机梯度下降,对数据随机采样本身会带来一个噪声,第二部分噪声是量化带来的噪声,可以进一步把量化噪声拆解开来,其中的每项是第l层的量化噪声对第k层的参数产生的影响(k<=l)。
量化的方差是跟量化到多少个桶(Bucket)成平方反比的关系。比如8bit的量化 ,就是把一个浮点数的数给分到了2的8次方,也就是256个桶里,那显然,量化的方差和桶的大小有关系的,而Minibatch Sampling跟量化是没有关系的。
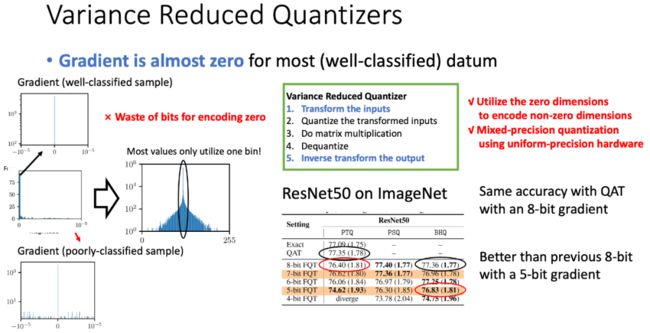
所以可以得到一个图表,看不同的算法用多少bit的时候梯度方差是多少。有项不随Bit变化的是Minibatch Sampling的方差(黑线)。对于每种量化算法,可以看到量化的方差会随着bit的缩小成指数增长,每少一个bit都会增大4倍的方差。所以如果采样方差远大于量化的方差,那么量化几乎不会对总体的梯度方差产生影响,也就是不会影响收敛,此时可以放心用低精度的梯度,不会对收敛产生任何影响。否则,当量化的方差比起采样方差不算小,比如占采样方差的10%,那这个时候量化就会显著的影响收敛了。并且这个时候每降低一个bit,方差都会增大4倍,所以把bit做到某一个阈值以后,再往下做就极为困难,是指数级困难的一件事。当然,更好的算法(绿线、蓝线)可以在同等的bit下做到更低的方差。
前面已经把量化方差的解析表达式给写出来了,那这时能不能根据这个理论改进量化算法?我们设计了一个带参数的量化器,然后推导出使得梯度方差最小的最优参数。这样的量化器在理论上是最优的。我们的量化方法利用了分类问题中梯度的稀疏性,实际上能在收敛后达到的准确率差不多的情况下,把梯度bit比原来降低3位。
小结一下,虽然全量化训练看似复杂,前后向传播都要做量化,但因为反向传播的链式法是一个线性操作,所以相对是比较容易分析的。
05
量化用于压缩
下面看一个压缩的场景。这里我们希望通过量化节省训练过程的内存消耗。内存花在哪里呢?在很多场景里面,内存主要是花在存储每层的激活(特征)上面。前向传播的时候,每层的激活都需要储存下来,因为这些激活在反向传播时还会用到。显然,存储代价和网络的宽度、深度、batch size等是成正比的。
我们采用的方法很简单,就是压缩这些存储的激活。前向传播的时候不存储全精度的激活,而是存一个压缩过的激活,比如说从32位压缩到2位,然后在反向传播算梯度之前,再把这些压缩的激活解压。和前面加速的算法一样,这个压缩算法也是近似的。本来算法用精确梯度去更新,由于量化的原因,计算梯度的时候用的是压缩过的近似激活,所以算出来的梯度也是近似的。用这个近似的梯度去做SGD又有什么理论保证呢?
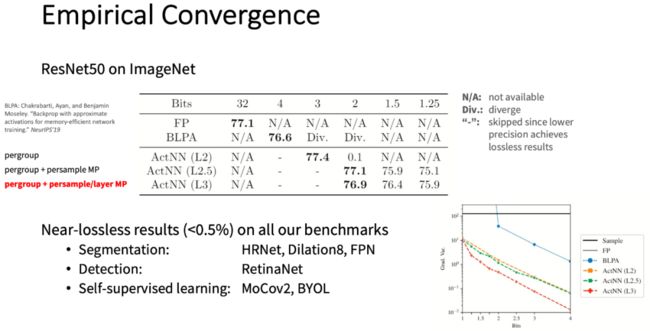
我们可以跟训练加速用相同的方法做分析。假设量化的量化器是无偏的,在这种情况下,可以得出近似梯度和精确梯度的误差,最终还是能保证收敛。收敛速度仍取决于梯度方差。我们提出了一些精巧的算法,能在不影响准确率和收敛速度的情况下,把激活压缩到2位。
压缩比加速是相较容易实现的,因为其不需要一个专门的低精度矩阵乘以它卷积的算子,不需要专门的硬件配合,有量化和反量化两个操作就够了。然后,我们把提出的压缩算法在PyTorch上做了一个实现,具体来说,我们实现了一些省内存的神经网络的层。每一层做前向传播的时候存储一些信息,来用到反向传播中,在存这个信息之前,对这个信息做了压缩,然后在反向传播的时候做解压缩。
当初开发该项目的时候,主要是针对视觉的卷积神经网络,现在我们也在开发一个更普遍的版本,可以支持任意的网络,包括Transformer。这个工具使用起来非常简单,只需要把原来的定义的一些PyTorch的层通过一个一键转换的方法来转换,在实际测试中能达到12倍内存的节省。
另外,我们还设计了精巧的量化的策略,在知道量化方差有多大的情况下,通过合理的去设计量化策略更好的最小化方差。我们的算法即使在量化到2bit的时候都不会损失精度,甚至更极端的时候达到1.25bit的时候才会损失精度,但仍然能够收敛。因为压缩比加速更容易实现,不需要压缩后的矩阵还能够高效的做乘法。
这个算法在同样的内存下可以比不做压缩好很多,并且可以和其他框架同时使用,也能在相同的内存下把模型的深度做得更深,可以放到内存的显存里面。
06
总结
总结一下,今天的报告想给大家传达的是能把大模型做得更好的一种方法,能够更快的训练,有更好的内存效率,可以缩小模型的大小,下载模型的时候只需要更小的网络带宽,而且在分布式训练的时候,可以降低通信开销。
另外,它跟其它的技术是正交的,可以同时使用的。不过,量化是一种有损的方法,可能要更好的考虑一下,这会不会损失精度,能不能收敛。不过,对于很多情况而言,把量化看作是无偏的随机的操作,是可以得到较好的理论保证的。
欢迎点击阅读原文参与文章讨论。