用深度学习完成3D渲染任务的蹿红

用深度学习完成3D渲染任务的蹿红

研究背景和研究意义

人类通过双眼来探索与发现世界。人类接收外部信息的方式中，有不到三成来自于听觉、触觉、嗅觉等感受器官，而超过七成、最丰富、最复杂的信息则通过视觉¹进行感知的。计算机视觉便是一种探索给计算机装备眼睛(摄像头)与大脑(算法)的技术，以使计算机能够自主独立的控制行为、解决问题，同时感知、理解、分析外部环境。

三维重建作为计算机视觉技术中最为最为热门的研究方向之一，涉及到包括图像处理、立体视觉、模式识别等多个学科体系。随着元宇宙(Metaverse)的崛起，构建虚拟的、可参与的、实时交互的3D环境的任务也接踵而至。如何在元宇宙的建设中对真实场景进行构建，以及如何还原出真实的色彩、纹理和更多的细节，从而给虚拟世界创造更好的沉浸式体验就成为了当前3D渲染的主要研究背景。

所谓渲染就是用计算机模拟这一过程，拍照对象是已存在的某种三维场景表示(3D representation of the scene)，形成照片的机制是图形学研究人员精心设计的算法。渲染的关键前提就是三维场景表示已经存在。渲染一词本身不包办生成三维场景表示，但是的确与三维场景表示的形式息息相关；因此研究渲染的工作通常包含对三维场景表示的研究。接下来我将首先带领大家简单的对三维重建方面知识进行了解，然后再进一步的进入我们今天的主题–渲染

基于传统多视图几何的三维重建算法

传统的三维重建传算法按传感器是否主动向物体投射光源可以分为主动式和被动式两种方法，其中主动式是指通过传感器主动地向物体照射信号，然后依靠解析返回的信号来获得物体的三维信息，常见的方法有结构光法、TOF激光飞行时间和三角测距法等等。被动式方面依靠多视图几何原理基于视差进行计算，主要方法有**SFM(struction from Motion)**等。

相机标定以及坐标转换

在说明传统的三维重建方法之前，我认为对相机标定以及如何从世界坐标系转换到像素坐标系做出一定的了解是有必要的。想要知道在空间物体表面某点的三维几何位置与其在图像中对应点之间的关系，必须建立相机成像的几何模型，其中几何模型的参数就是相机参数，求解相机参数的过程就是相机标定。

那么如何实现3D世界和2D世界的相互转换呢？我们要知道在转换的过程中存在四个坐标系，分别是世界坐标系、相机坐标系、图像坐标系以及像素坐标系。3D与2D的转换也就是透过这四个坐标系进行转换，首先从世界坐标系到相机坐标系的变换，只需要对物体进行旋转和平移。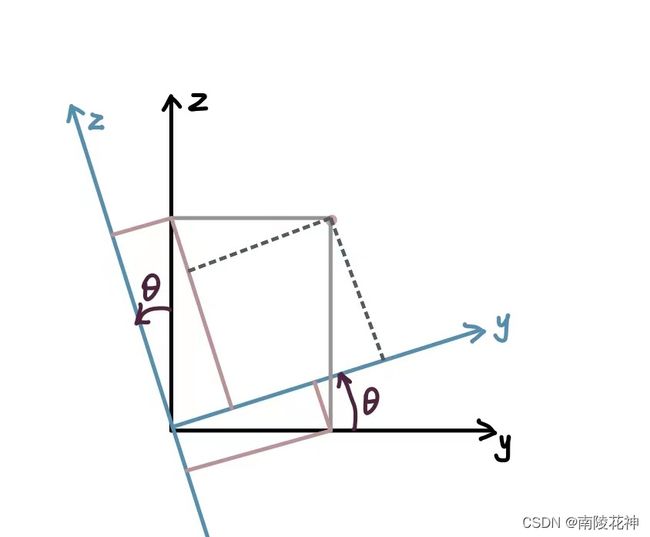
若以x为轴进行旋转，其中：(同理可知绕y轴和绕z轴所得到的旋转矩阵）
X_c=X；
Y_c=cosθ·Y+sinθ·Z；
Z_c=-sinθ·Y+cosθ·Z；我们可以得到矩阵如下所示：

我们将旋转矩阵假定为R，平移矩阵为T，就可以得到完整的坐标变化公式：(当中的系数矩阵也被称作为相机的外参矩阵）

从相机矩阵到图像矩阵的变换就是从三维立体空间到二维平面空间的变换，所反映的是空间中任一点P与图像上任一点P之间的关系，如下图2所示：

由三角形相似我们可以得到以下等式：

从而得到以下变换矩阵==(齐次坐标表示）== （其中p代表picture；c代表camera；s代表点p在相机矩阵中z方向的坐标）

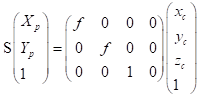
从图像坐标系到像素坐标系这部分比较简单，如下图所示：

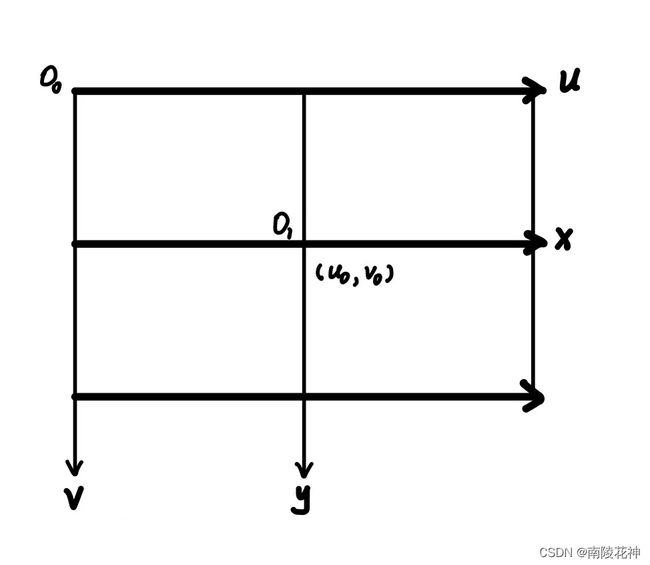
我们可以得到矩阵变换如下：(d_x 为每个像素的物理尺寸）

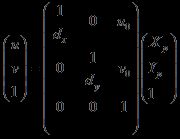
主动式——结构光法

有了以上的相机标定等知识的基础，我们就可以对结构光法进行更好的理解。结构光法依靠投影仪将编码的结构光投射到被拍摄物体上，然后由摄像头进行拍摄。由于被拍摄物体上的不同部分相对于相机的距离精度和方向不同，结构光编码的图案的大小和形状也会发生改变。这种变化可以被摄像头捕获，然后通过运算单元将其换算成深度信息，进而获取物体的三维轮廓信息。

投影光编码的方式有很多种，通常的编码是分别对投影图片的行和列进行编码，常见的格雷码如下图所示：

通过对相机图片上拍摄的物体表面投射的列格雷码光编码及行格雷码光编码进行解码，就可以知道物体在相机图片上成像位置(u_c，v_c)及其对应的投影仪虚拟的成像位置(u_p，v_p)，则上述方程可以改为：(其中K为相机的内参，S为真实点在相机矩阵中的z坐标。


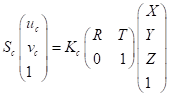
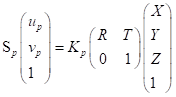
这种方法缺点是容易受环境光干扰，因此室外体验差。另外，随检测距离增加，其精度也会变差。目前，一些研究通过增大功率、改变编码方式等形式解决这些问题，取得了一定的效果。

主动式——TOF激光飞行时间&三角测距法

TOF 飞行时间法依靠通过向目标连续发送光脉冲，然后依据传感器接收到返回光的时间或相位差来计算距离目标的距离。但显然这种方式足够的精度需要极为精确的时间测量模块，因此成本相对较高。好处是这种方法测量距离比较远，受环境光干扰比较小。目前这方面研究旨在降低计时器良品率及成本，相应的算法性能也在提升。

三角测距法，即依据三角测距原理，不同于前两者需要较为精密的传感器，三角测距法整体成本较低，并且在近距离的时候精度较高，因而广泛应用于民用和商用产品中，如扫地机器人中。但三角测距的测量误差与距离有关，随着测量距离越来越大，测量误差也越来越大，这是由三角测量的原理导致的，不可避免。

被动式——SFM(struction from Motion）

SFM算法是一种基于各种收集到的无序图片进行三维重建的离线算法²，是一种单目(仅使用一个相机进行三维重建)的一种方法，其流程如下所示：
1、相机标定，获取相机内参
2、使用标定好的相机从多个角度拍摄同一场景图片，并按序号保存
3、对相邻图像两两计算匹配特征点；一般首先使用两张图像进行重建，计算出一个初始的点云，之后不断添加后续的图像，具体添加哪一张图像的方法是：检查已有的图像中哪一个与已有点云中的点匹配最多，就选哪一张。
4、使用3中计算好的对应点对计算基础矩阵F
5、通过基础矩阵计算本征矩阵
6、通过本征矩阵计算两个视角之间的运动，即R，T；但是由于符号的关系，会解出四种可能的[R|T]矩阵，因此，我们需要将所有的2D的点使用这四种映射分别映射到3D空间中去，看哪一种映射对应的3D点的z深度方向全部是正确的，因此，准确的[R|T]会使得所有的场景点都在相机朝向的正前方
7、在计算出[R|T]矩阵后，就可以使用光学三角法对所有的特征点重建了

基于深度学习的三维重建方法

在传统三维重建算法中引入深度学习方法进行改进

因为CNN在图像的特征匹配上有着巨大优势，所以这方面的研究有很多，比如：DeepVO³ ，其基于深度递归卷积神经网络（RCNN）直接从一系列原始RGB图像（视频）中推断出姿态，而不采用传统视觉里程计中的任何模块，改进了三维重建中的视觉里程计这一环。BA-Net⁴ ，其将 SfM 算法中的一环集束调整（Bundle Adjustment,BA）优化算法作为神经网络的一层，以便训练出更好的基函数生成网络，从而简化重建中的后端优化过程。Code SLAM⁵ ，如之前所提，其通过神经网络提取出若干个基函数来表示场景的深度，这些基函数可以简化传统几何方法的优化问题。

深度学习重建算法和传统三维重建算法进行融合，优势互补

CNN-SLAM将CNN预测的致密深度图和单目SLAM的结果进行融合，在单目SLAM接近失败的图像位置如低纹理区域，其融合方案给予更多权重于深度方案，提高了重建的效果。

模仿动物视觉，直接利用深度学习算法进行三维重建

我们知道，三维重建领域主要的数据格式有四种：
深度图（depth map），2D图片，每个像素记录从视点到物体的距离，以灰度图表示，越近越黑；
体素（voxel），体积像素概念，类似于2D之于像素定义；
点云（point cloud），每个点逗含有三维坐标，乃至色彩、反射强度信息；
网格（mesh），即多边形网格，容易计算。
因而，依据处理的数据形式不同我们将研究简要分为三部分：1）基于体素；2）基于点云；3）基于网格。而基于深度图的三维重建算法暂时还没有，因为它更多的是用来在2D图像中可视化具体的三维信息而非处理数据。

基于体素

体素，作为最简单的形式，通过将2D卷积扩展到3D进行最简单的三维重建⁶，基于体素形式，其直接用单张图像使用神经网络直接恢复深度图方法，将网络分为全局粗估计和局部精估计，并用一个尺度不变的损失函数进行回归。

3D-R2N2模型⁷使用Encoder-3D LSTM-Decoder的网络结构建立2D图形到3D体素模型的映射，完成了基于体素的单视图/多视图三维重建(多视图的输入会被当做一个序列输入到LSTM中，并输出多个结果)。

但这种基于体素的方法存在一个问题，提升精度即需要提升分辨率，而分辨率的增加将大幅增加计算耗时（3D卷积，立次方的计算量）。

基于点云

相较而言，点云是一种更为简单，统一的结构，更容易学习，并且点云在几何变换和变形时更容易操作，因为其连接性不需要更新。但需要注意的是，点云中的点缺少连接性，因而会缺乏物体表面信息，而直观的感受就是重建后的表面不平整。

如何用恰当的损失函数来进行衡量一直是基于深度学习用点云进行三维重建方法的难题，通过相同的几何形状可能在相同的近似程度上可以用不同的点云表示⁸解决了训练点云网络时候的损失问题。

同时，通过对场景的点云进行处理，融合三维深度和二维纹理信息，提高了点云的重建精度⁹。

基于网格

我们知道之前的方法的缺点：
基于体素，计算量大，并且分辨率和精度难平衡
基于点云，点云的点之间缺少连接性，重建后物体表面不光滑
相较而言，网格的表示方法具有轻量、形状细节丰富的特点，重要是相邻点之间有连接关系。因而研究者基于网格来做三维重建。我们知道，网格是由顶点，边，面来描述3D物体的，这正好对应于图卷积神经网络的 M=（V,E,F） 所对应。Pixel2Mesh ¹⁰，用三角网格来做单张RGB图像的三维重建，相应的算法流程如下：
（1）对于任意的输入图像都初始化一个椭球体作为初始三维形状。
（2）然后网络分为两部分： 一部分用全卷积神经网络来提取输入图像的特征；另一部分用图卷积网络来表示三维网格结构，模型通过四种损失函数来约束形状，取得了很好的效果。贡献在于用端到端的神经网络实现了从单张彩色图直接生成用网格表示的物体三维信息。

传统的渲染方法——前NeRF时代

光栅化渲染

传统的渲染方法包括光栅化，光线追踪等等，都是对照相机拍照的光学过程进行数学物理建模来实现的¹¹。
首先，光栅化渲染分为以下几个阶段：应用程序阶段、几何阶段和光栅化阶段。在应用程序阶段通常可以实现的有碰撞检测、加速算法、输入检测，动画，力反馈以及纹理动画，变换、仿真、几何变形，以及一些不在其他阶段执行的计算，如层次视锥裁剪等加速算法就可以在这里实现。几何阶段中完成的步骤有模型试点变换、顶点着色、投影、剪裁和屏幕映射等等。光栅化阶段是在给定经过变换和投影之后的顶点，颜色以及纹理坐标（均来自于几何阶段），给每个像素正确配色，以便正确绘制整幅图像。主要阶段有三角形设定阶段、三角形遍历阶段、像素着色阶段和融合阶段。
对于光栅化的解释，我认为可以总结为两个字：“投影”。和计算机图形学中的投影类似，也都考虑了非理想情况的影响，其中包括畸变、像差、渐晕、散焦模糊以及相互反射等影响因素¹² （在这里我们不做讨论）。我们所看到的三维物体可以被定义为是连续的，那么二维的图像就可以被定义为是离散的，所谓的离散和连续就比如我们在两点之间用笔点出很多个点，虽然都是单独分散的点，但是放远看了，发现这一堆点也近似是连续的一条线，但是本质上这条线是一个个分散点组成的。

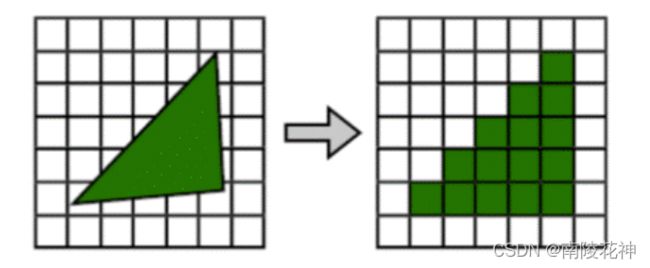
==那么三维物体的颜色是怎么被图片呈现的呢？就简单而论，你就试想这个三维物体是个球体，球体就长红色的，每个地方的RGB值都是（255,0,0），复杂而论，就是三维物体上的每个顶点的颜色值都是用着色器计算出来的，属于更进一步的内容，这里了解即可。着色需要在投影前完成。
== “离散”的屏幕无法直接显示“连续”的三维物体，因此需要先对连续的物体进行“离散化”，离散化就是对三维物体的采样点进行投影，结果存到帧缓存上（存储一帧画面的像素值），再将帧缓存交给显卡，显示一副图像。其中投影需要借助投影矩阵，也就是我们之前介绍过的矩阵来完成。有了投影矩阵，就能将三维物体上的颜色值映射到我们的帧缓存上，然后将这个帧缓存交给我们的GPU来读取显示到显示屏上，这就叫光栅渲染。
光栅化的固有缺点就是使用各种技巧对显示世界进行模拟，就像一个小孩学大人说话，别人一听就会觉得孩子怎么这么成熟，实际上他并不理解内容的意义，换一种语境就会变得滑稽可笑。从根本上解决这一问题，还是需要光追技术，因为这种技术与现实中光线传播的方式基本一致。通过模拟光的实际行为，提供比光栅化逼真的多的结果。比如：有正确半影区的阴影、更精细的全局光照、折射、投射等效果。

光线追踪渲染

光栅化是一种前馈过程，在这个过程中，几何体被转换到图像域。而光线追踪是光线从图像像素向后投射到虚拟场景中，通过反射和折射与几何体的交点来递归的投射新光线来进行模拟的过程。
试想一下，我们人眼能看到外面世界，是因为有光，如果我们晚上在封闭的房间关掉所有的灯，那我们什么也看不见，是因为没有光进入我们的眼睛。光线追踪就是想模拟这个情景，追踪每条光线的传播行为，计算每条光线对我们人眼观察的贡献值，即颜色值。如下图所示：

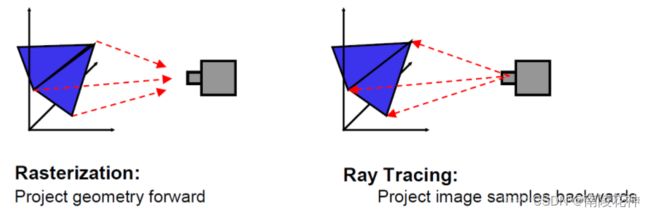
由于外界光线并不是全部能映射到我们的眼睛中，所以我们只需要模拟那些进入我们眼睛的光线，我们知道，光线是可逆的，所以我们将光线的起点改为从我们人眼出发，去寻找场景中的光源，这样连起来就是一条从连接了人眼和光源的光路，是一条用的光线。这样就将问题从原来多个光源对应多个发射点，简化成了仅有我们人眼一个发射点，不管场景中布置了多少个光源，我们都只要考虑从我们人眼出发追踪光线就行了。

神经网络侵略3D渲染任务：NeRF呼之欲出 (重点)

通过硬件加速的渲染通常依赖于光栅化的方式，因为光栅化具有良好的内存一致性。然而，对于许多像复杂的光线、景深、运动模糊等真实世界的图像效果来说，使用光线追踪技术往往会获得更好的效果。NVidia公司最近发布的GPU¹³ 具有很好的渲染加速结构，可以在实时的图像渲染过程中使用光线追踪技术。
光栅化渲染需要显式的几何表示，然而光线追踪可以使用隐式场来表示。隐式表示¹⁴ 也可以转化为显式形式从而进行光栅化渲染，渲染器还可以同时使用光栅化和光线追踪，来获得更高的效率和更真实的渲染效果¹⁵ 。但是通过光栅化和光线追踪来渲染的图像质量很大程度上取决于所使用的数学模型。从真实世界中得到不同的模型参数，比如：相机角度、物体的几何表现、物体的材质、灯光等的过程被称作反向渲染^{16 17 18 19 20} 。3D神经渲染的一个关键特性是在训练的过程中，将投影与图像的形成于3D场景表示分离。这种解纠缠在图像合成中可以实现3D一致性，为了实现这种解纠缠，神经渲染通常依赖于传统的渲染方式（光珊化、光线追踪）中的物理学²¹ 。

反向渲染与神经渲染密切相关，最早使用神经渲染这一术语的论文是GQN²²。反向渲染的一个缺点是在经典的渲染（光栅化、光线追踪）中，由于数学物理模型建模的复杂性和昂贵的计算开销，并不能使用预定义的模型来准确的再现复杂的真实世界中所有的特征。相比之下，神经渲染将可学习的模型引入到渲染管道中，以代替此类模型。深度神经网络可以在统计上近似这种物理过程，从而使输出与训练数据更接近，比反向渲染更准确地再现一些现实世界的效果。

GANS

与传统的渲染方式相比，深度神经网络可以从大量的数据集中进行学习，而传统的渲染方式使用的是比较小的数据集（几百至几千）。因此，神经渲染的主要障碍之一就是如何创建物体，创建几何物体的表面、光线、材质等内容往往需要大量繁琐而昂贵的手工工作。GANs应运而生，由Goodfellow等人创建的GANs²³ 在近年逐渐演变成为用于创建高分辨率的图像^{24 25 26} 及高清的视频^{27 28} 。在最近的工作中可以合成与正常人脸无法区分的高分辨率人脸图像²⁹ 。

深度神经网络擅长通过训练生成与训练集相似的随机真实图像，然而，完全的随机并不适用，用户控制与用户交互性在图像合成中起着关键性的作用³⁰ 。因此，GANs模型需要拓展一个条件设置，以获得对图像合成的显式控制³¹ （cGAN）。前期的工作是针对于每个像素进行训练，通过前馈的神经网络得到每个像素的距离³² 。但是我们知道图像的每个像素之间是存在一定的联系的，我们独立的考虑每个像素忽略了视觉结构的复杂性，所以得到的结果往往是模糊的^{33 34}。为了解决这个问题，最近的研究提出了感知距离（Perceptual Distance）^{35 36 37} 作为图像的评价指标。这种图像评估方式广泛的应用在艺术风格化 ^{38 39} 、图像生成与合成⁴⁰ 以及超分辨率图像的生成^{41 42} 。

隐式场景表示

NeRF（神经体渲染）的直接先驱是使用神经网络隐式表示三维场景。许多3D-aware的图像生成方法使用体素、网格、点云等形式表示三维场景，通常基于卷积架构。 但在 CVPR 2019 上，开始出现使用神经网络拟合标量函数来表示三维场景的工作^{43 44 45 46}。一些有关于隐式函数的论文也成为NeRF的先驱：Structured Implicit Functions⁴⁷ 展示了一种通过将隐式表达简单相加的方式来进行组合; CvxNet⁴⁸ 提出了一种基于原始分解的几何表示方法,通过少量凸形元素来近似几何，同时力求从数据自动推断低维表示，而无需人工监督。Implicit Differentiable Renderer⁴⁹ 提出了一种具有更复杂的光场表示的结构，并且可以在训练期间优化相机姿势。其中DeepSDF⁵⁰ 或许是最接近NeRF的前驱工作了。SDF是（Signed Distance Function）的缩写。DeepSDF通过回归（regress）一个分布来表达三维表面的。

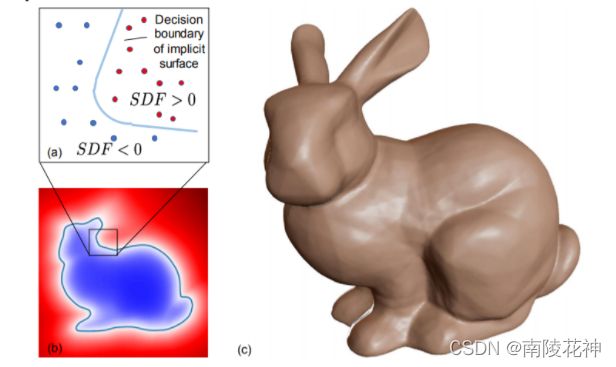
SDF>0的地方，表示该点在三维表面外面；SDF<0的地方，表示该点在三维表面里面。回归这一分布的神经网络是多层感知机（Multi-Layer Perceptron，MLP），非常简单原始的神经网络构。NeRF比DeepSDF进步的地方就在于，NeRF用RGB，σ代替了SDF，所以除了能推理一个点是否在物体表面，还能推理RGB颜色和透明度，且颜色是view-dependent的（观察视角不同，同一物点的颜色不同），从而实现功能更强大的渲染。

NeRF！！！

2020年可以被称作是神经渲染的元年，由Mildenhall等人提出的NeRF⁵¹ 使人们眼前一亮，Nerual Volumes⁵²首次对神经体渲染进行了介绍，它就是对体密度和颜色进行了积分，通过体渲染得到二维的图像。本质上，NeRF采用DeepSDF的架构 ，但是就像我们所说的，NeRF用（RGB，σ）代替了SDF。接下来将对NeRF做代码级别的解读。
什么是Nerf？(Neural Radiance Field）神经辐射场是他的全称。通俗来讲，就是构造一个隐式的渲染流程，其输入是某个视角下发射的光线的位置o，方向d以及对应的坐标(x,y,z)。通过神经辐射场F_θ，得到体密度和颜色，最后再通过渲染得到最终的图像。
NeRF的在训练中输的数据是：从不同位置拍摄同一场景的图片，拍摄这些图片的相机位姿、相机内参，以及场景的范围。若图像数据集缺少相机参数真值，作者便使用经典SFM重建解决方案COLMAP⁵³ 估计了需要的参数，当作真值使用。
在训练使用NeRF渲染新图片的过程中，先将这些位置输入MLP以产生volume density和RGB颜色值；取不同的位置，使用体积渲染技术将这些值合成为一张完整的图像；因为体积渲染函数是可微的，所以可以通过最小化上一步渲染合成的、真实图像之间的差来训练优化NeRF场景表示。这样的一个NeRF训练完成后，就得到一个 以多层感知机的权重表示的 模型。一个模型只含有该场景的信息，不具有生成别的场景的图片的能力。
==除此之外，NeRF还有两个优化的trick：==位置编码（positional encoding），类似于傅里叶变换，将低维输入映射到高维空间，提升网络捕捉高频信息的能力；体积渲染的分层采样（hierarchical volume sampling），通过更高效的采样策略减小估算积分式的计算开销，加快训练速度。
在我们可以实现从像素矩阵到世界矩阵的变换之后，我们就可以得到想要的origins；directions；lengths和xy_gird。
1、根据H，W计算得到n_rays_per_image=H*W
2、uniform的生成n_pts_per_ray（64）个depth（在min(2)和max(6)之间的均匀采样）

class GridRaysampler(torch.nn.Module):
    """
    Samples a fixed number of points along rays which are regularly distributed
    in a batch of rectangular image grids. Points along each ray
    have uniformly-spaced z-coordinates between a predefined
    minimum and maximum depth.

    The raysampler first generates a 3D coordinate grid of the following form:
    ```
       / min_x, min_y, max_depth -------------- / max_x, min_y, max_depth
      /                                        /|
     /                                        / |     ^
    / min_depth                    min_depth /  |     |
    min_x ----------------------------- max_x   |     | image
    min_y                               min_y   |     | height
    |                                       |   |     |
    |                                       |   |     v
    |                                       |   |
    |                                       |   / max_x, max_y,     ^
    |                                       |  /  max_depth        /
    min_x                               max_y /                   / n_pts_per_ray
    max_y ----------------------------- max_x/ min_depth         v
              < --- image_width --- >
    ```

    In order to generate ray points, `GridRaysampler` takes each 3D point of
    the grid (with coordinates `[x, y, depth]`) and unprojects it
    with `cameras.unproject_points([x, y, depth])`, where `cameras` are an
    additional input to the `forward` function.

3、从NDC空间设两个平面（图2空间中）通过将其映射回world/camera坐标系，得到光线的方向（ray_directions_world)和原点位置（rays_origins_world)
4、output：
origins（batchsize，H，W，3）
directions（batchsize，H，W，3）
lengths（batchsize，H，W，64）
xy_gird
注意第二步中在深度上取64个点是均匀采样，但是实际上物体在世界坐标系中并不是均匀的，应该变成间隔不一致的结构，以下函数用来完成此步骤：

def _stratify_ray_bundle(self, ray_bundle: RayBundle):
        """
        Stratifies the lengths of the input `ray_bundle`.

        More specifically, the stratification replaces each ray points' depth `z`
        with a sample from a uniform random distribution on
        `[z - delta_depth, z+delta_depth]`, where `delta_depth` is the difference
        of depths of the consecutive ray depth values.

        Args:
            `ray_bundle`: The input `RayBundle`.

        Returns:
            `stratified_ray_bundle`: `ray_bundle` whose `lengths` field is replaced
                with the stratified samples.
        """
        z_vals = ray_bundle.lengths
        # Get intervals between samples.
        mids = 0.5 * (z_vals[..., 1:] + z_vals[..., :-1])
        upper = torch.cat((mids, z_vals[..., -1:]), dim=-1)
        lower = torch.cat((z_vals[..., :1], mids), dim=-1)
        # Stratified samples in those intervals.
        z_vals = lower + (upper - lower) * torch.rand_like(lower)
        return ray_bundle._replace(lengths=z_vals)

神经辐射场

对第一步得到的rays调用volumetric函数，得到rays_densities和rays_features(也就是体密度和RGB）

 def forward(
        self, 
        ray_bundle: RayBundle,
        **kwargs,
    ):
        """
        The forward function accepts the parametrizations of
        3D points sampled along projection rays. The forward
        pass is responsible for attaching a 3D vector
        and a 1D scalar representing the point's 
        RGB color and opacity respectively.
        
        Args:
            ray_bundle: A RayBundle object containing the following variables:
                origins: A tensor of shape `(minibatch, ..., 3)` denoting the
                    origins of the sampling rays in world coords.
                directions: A tensor of shape `(minibatch, ..., 3)`
                    containing the direction vectors of sampling rays in world coords.
                lengths: A tensor of shape `(minibatch, ..., num_points_per_ray)`
                    containing the lengths at which the rays are sampled.

        Returns:
            rays_densities: A tensor of shape `(minibatch, ..., num_points_per_ray, 1)`
                denoting the opacity of each ray point.
            rays_colors: A tensor of shape `(minibatch, ..., num_points_per_ray, 3)`
                denoting the color of each ray point.
        """
        # We first convert the ray parametrizations to world
        # coordinates with `ray_bundle_to_ray_points`.
        rays_points_world = ray_bundle_to_ray_points(ray_bundle)
        # rays_points_world.shape = [minibatch x ... x 3]
        
        # For each 3D world coordinate, we obtain its harmonic embedding.
        embeds = self.harmonic_embedding(
            rays_points_world
        )
        # embeds.shape = [minibatch x ... x self.n_harmonic_functions*6]
        
        # self.mlp maps each harmonic embedding to a latent feature space.
        features = self.mlp(embeds)
        # features.shape = [minibatch x ... x n_hidden_neurons]
        
        # Finally, given the per-point features, 
        # execute the density and color branches.
        
        rays_densities = self._get_densities(features)
        # rays_densities.shape = [minibatch x ... x 1]

        rays_colors = self._get_colors(features, ray_bundle.directions)
        # rays_colors.shape = [minibatch x ... x 3]
        
        return rays_densities, rays_colors

位置编码

为了让MLP更好的捕捉高频信息，我们对p点的坐标（x,y,z）和direction（方向）进行了位置编码（维度提升），如下图4所示：

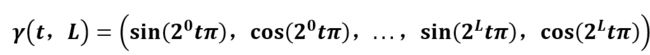
对（x，y，z）的编码长度L为10；对direction的编码长度为4

得到体密度

对应成员函数：self._get_densities
具体步骤如下：
1、我们将第一步中得到的origins和direction进行处理，带入到camera ray r(t)=o+td,可以得到
ray_points_world(batchsize,1024,64,3) 其中1024是对HW个像素点的采样，64就是第一步中ray中depth上不均匀采样的64个点。
2、对ray_points_world进行位置编码，得到(batchsize,1024,64,63),其中63=102*3+3。10指编码长度L；2是xy；3是方向向量，+3保留自己
3、丢到MLP中，input的维度是63，经过若干中间层(self.intermediate_layer)的自定义参数256，最终输入(256,1)得到output_dim，得到[0,1]范围内的densities (batchsize,1024,64,1)。

def _get_densities(self, features):
        """
        This function takes `features` predicted by `self.mlp`
        and converts them to `raw_densities` with `self.density_layer`.
        `raw_densities` are later mapped to [0-1] range with
        1 - inverse exponential of `raw_densities`.
        """
        raw_densities = self.density_layer(features)
        return 1 - (-raw_densities).exp()

得到color

对应成员函数self._get_colors由于体密度与方向无关，所以并不需要对direction进行特征提取，但是对于color来说，不同的视角会造成不同的效果，所以对color来说，要使用同一个FC层，来同时对xyz的feature和经过位置编码后的ray_direction进行处理，之所以要使用同一个FC层，是为了将体密度和方向进行联系。具体步骤如下：
1、input：经过self.intermediate_layer得到的结果(batchsize,1024,64,256)
2、input：经过位置编码后的direction**(batchsize,1024,27)；27同63
3、output：(batchsize,1024,64,128)
4、output：(batchsize,1024,1,128)
5、最终该结果将output1和output2进行相加，得到每个ray上(1024)的每个点(64)上面的特征(128)，并加上该ray方向上的编码特征，然后进行RELU，FC(128,3)处理后(Sigmoid)，最终得到[0，1]范围内的rays_rgb(batchsize,1024,64,3)。

def _get_colors(self, features, rays_directions):
        """
        This function takes per-point `features` predicted by `self.mlp`
        and evaluates the color model in order to attach to each
        point a 3D vector of its RGB color.
        
        In order to represent viewpoint dependent effects,
        before evaluating `self.color_layer`, `NeuralRadianceField`
        concatenates to the `features` a harmonic embedding
        of `ray_directions`, which are per-point directions 
        of point rays expressed as 3D l2-normalized vectors
        in world coordinates.
        """
        spatial_size = features.shape[:-1]
        
        # Normalize the ray_directions to unit l2 norm.
        rays_directions_normed = torch.nn.functional.normalize(
            rays_directions, dim=-1
        )
        
        # Obtain the harmonic embedding of the normalized ray directions.
        rays_embedding = self.harmonic_embedding(
            rays_directions_normed
        )
        
        # Expand the ray directions tensor so that its spatial size
        # is equal to the size of features.
        rays_embedding_expand = rays_embedding[..., None, :].expand(
            *spatial_size, rays_embedding.shape[-1]
        )
        
        # Concatenate ray direction embeddings with 
        # features and evaluate the color model.
        color_layer_input = torch.cat(
            (features, rays_embedding_expand),
            dim=-1
        )
        return self.color_layer(color_layer_input)

好的，现在我们得到了我们想要的rays_densities和rays_colors,那么我们又可以开始愉快的下一步啦

体渲染

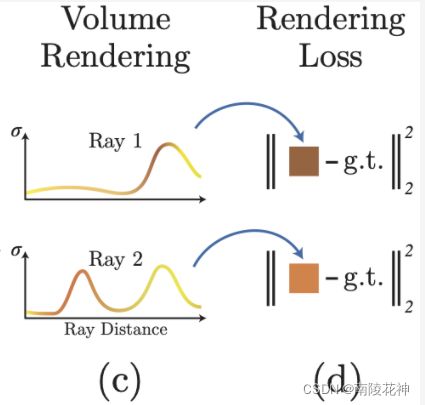
如何对前面得到的rays_densities和rays_features进行融合？使之成为人眼可以接受的图像呢？这就要提到raymarcher函数

images=self.reymarcher(
	rays_denstites=rays_densities,
	rays_features=rays_features,
	ray_bundle=ray_bundle,
	**kwargs
)
#images - minibatch x ... x (feature_dim+opacity_dim)
return images,ray_bundle

体渲染又称作volume rendering，对于一条线的颜色，我们可以用积分的方式表达如下：

这么看起来好像有点不知所云，我来具体解释一下这个公式的含义
C®：表示每条光线ray的颜色
σ(x)：体素密度，可以理解为一条射线r在经过x处的一个无穷小的粒子时被终止的概率，也就是这个点的不透明度
r(t)：o+td，这里o是射线原点，d是direction，也就是相机的一条射线
t_f，t_n：t的近端和远端边界分别为t_n以及t_f
T(t)：是射线从t_n和t_f这一段路径上的累计透明度，可以被理解为一路上没有集中任何粒子的概率，具体形式为

但是实际中并不能对Nerf进行连续的点的估计，所以上述的T(t)也就不服存在，转而替换成为将射线需要积分的区域分为N份，然后在每一个小区域中进行均匀随机采样。这样的方式能够在只采样离散点的前提下，保证采样位置的连续性。第i个采样点可以表示为：

于是我们可以将颜色的积分转化为求和公式如下

多层级体素采样

Nerf的渲染过程计算量很大，每条射线都要采样很多店。但是实际上，一条射线上大部分是空白区域，或者是被遮挡的区域，因此作者采用了一种”coarse to fine"的形式，同时优化coarse网络和fine网络。
对于coarse网络，我们可以采样较为记住的N_c个点，并将前述的离散求和函数重新表示为：

其中
接下来可以对w做归一化

此处的w_i (weights)可以看作是沿着射线的概率密度函数，具体来说就是rays_densities*(batchsize,1024,64)得到的概率密度函数，当weights比较小时就表示对当前颜色的贡献比例小。
流程的输入输出如下
1、input：体密度(ray_densities) (batchsize,1024,64,1)
2、input：颜色(rays_colors) (batchsize,1024,64,3)
3、output：features(batchsize,1024,3)
4、output：weights(batchsize,1024,64)
最终得到的features=weights*ray_features(ray_colors)的和

后NeRF时代——GIRAFFE （2021CVPR最佳论文）

==我们在前面提到过GANS的诞生不仅是为了解决神经渲染所需要的大数据集问题，==同时还对形状外表的可控性提出了可能。由于NeRF并不能对三维物体的形状、外观等进行符合人意愿的改变，所以最近有研究将GAN与NeRF结合，GRAF⁵⁴ 应运而生。

GRAF

GRAF（Generative Radiance Fields）生成辐射场，研究的起因如下：在3D感知图像生成（3D-aware image synthesis）这一领域中（差不多都基于GAN），把三维的物体进行离散化的表示，比如PlatonicGAN⁵⁵ 的体素表示， HoloGAN⁵⁶ 的三维特征表示，体素表示法会限制分辨率，分辨率升高时会占用内存，并且产生可见的伪影（artifacts），特征表示法虽然好一点，但是需要额外学习如何渲染，把抽象的三维特征映射到二维的RGB数值，导致了特征很难解耦，在高分辨率下很难保持视图一致性。

而NeRF那样的模型，虽然三维重建的效果不错，但是缺点在于：需要大量的同一个场景物体的不同角度拍摄数据，这些数据还得有三维标注（相机位姿）；无法自由编辑重建物体。所以，GRAF算是在NeRF工作的基础上，结合了GAN进行了一番研究工作，这样就能使用二维监督的方式进行三维重建（也就是说仅仅需要同一物体的不同角度照片即可，不再需要相机位姿参数），让GAN去猜相机位姿势啥样的，并且对物体的形状与颜色可控性上面做了一定贡献。

…

…

…

…

…（具体方法暂不介绍 ）
但是GRAF仅能对场景中的单一物体进行渲染，无法有效的处理多物体的情况。

GIRAFFE

了解了NeRF和GRAF的工作之后，GIRAFFE的工作理解起来就很容易了。论文题目：Representing Scenes as Compositional Generative Neural Feature Fields⁵⁷ ，我们先来分析一下，是使用组合的生成神经特征场来表示一个多物体场景，与GRAF的不同的地方有两个关键词：组合的、特征场。实际上，与GRAF不同的地方也主要有两处：
1、组合的：把GRAF使用一整个模型才能表示的场景给组合起来， 也就是说场景中有多少个物体，就用多少个GRAF，有效地解决处理多物体重建时无法自由编辑每个单一物体的情况。
2、特征场：与GRAF不同，最终分别使用GRAF表示单个物体的时候，因为后面还要把他们组合起来，所以把采样点的颜色替换成颜色特征，然后组合成一个新的特征图，之后再使用设计的神经网络渲染渲染出最终RGB图像。
给定一个有多个物体的三维场景，许多场景合成方法的解耦操作是在2D空间进行的，没有考虑到场景实际上是3维的，因此会导致编辑物体的时候产生问题。

如第一行所示，许多没有在他们方法里考虑物体的三维属性的方法，操作多物体场景时，比如只想把左边的物体往前移动，结果导致的右边的物体产生了变化，这便是没有有效地将特征解耦。而GIRAFFE因此有两个灵感来源（insight）：
1、将合成的3D场景表示直接融入生成模型中，可以实现更可控的图像合成
2、将这种显式的3D表示（体渲染得到的特征图）与神经渲染相结合，可以更快地进行推断，使图像更加真实
…

…

…

…（具体方法暂不介绍）

总结

…（还有待总结）

参考文献

[1] Szeliski R. Computer vision: algorithms and applications[M]. Berlin: Springer, 2010.

[2] Ullman S. The interpretation of structure from motion[J]. Proceedings of the Royal Society of London. Series B.
Biological Sciences, 1979,203(1153):405-426.DOI:10.1098/rspb.1979.0006.

[3] Wang S, Clark R, Wen H, et al. DeepVO: Towards end-to-end visual odometry with deep Recurrent Convolutional Neural Networks, 2017[C].May.

[4] Tang C, Tan P. BA-Net: Dense Bundle Adjustment Network[J]. CoRR, 2018,abs/1806.04807.

[5] Bloesch M, Czarnowski J, Clark R, et al. CodeSLAM—Learning a Compact, Optimisable Representation for Dense Visual SLAM: IEEE Conference on Computer Vision and Pattern Recognition(CVPR), 2018[C]. IEEE.

[6] Eigen D, Puhrsch C, Fergus R. Depth Map Prediction from a Single Image using a Multi-Scale Deep Network: Advances in Neural Information Processing Systems (NIPS), 2014[C]. Curran Associates, Inc…

[7] Choy C B, Xu D, Gwak J, et al. 3D-R2N2: A unified approach for single and multi-view 3d object reconstruction, 2016[C]. Springer.

[8] Fan H, Su H, Guibas L J. A Point Set Generation Network for 3D Object Reconstruction From a Single Image, 2017[C].July.

[9] Chen R, Han S, Xu J, et al. Point-Based Multi-View Stereo Network, 2019[C].October.

[10] Wang N, Zhang Y, Li Z, et al. Pixel2Mesh: Generating 3D Mesh Models from Single RGB Images, 2018[C].September.

[11] Tewari A, Fried O, Thies J, et al. State of the art on neural rendering[C]//Computer Graphics Forum. 2020, 39(2): 701-727.

[12] Peter Sturm; Srikumar Ramalingam; Simone Gasparini; João Barreto, Camera Models and Fundamental Concepts Used in Geometric Computer Vision , now, 2011.
[13]
[14] Haines E., Akenine-Moller T. (Eds.): Ray Tracing Gems.Apress, 2019.

[15] Lorensen W E, Cline H E. Marching cubes: A high resolution 3D surface construction algorithm[J]. ACM siggraph computer graphics, 1987, 21(4): 163-169.

[16] Mcguire M., Mara M.: Efficient GPU screen-space ray tracing. Journal of Computer Graphics Techniques (JCGT) 3, 4 (December 2014), 73–85.

[17] Marschner S. R.: Inverse rendering for computer graphics. Citeseer, 1998. 4

[18] Deschaintre V, Aittala M, Durand F, et al. Flexible svbrdf capture with a multi‐image deep network[C]//Computer graphics forum. 2019, 38(4): 1-13.

[19] Henzler P, Mitra N, Ritschel T. Escaping plato’s cave using adversarial training: 3d shape from unstructured 2d image collections[C]//Proceedings of the International Conference on Computer Vision 2019 (ICCV 2019). IEEE, 2019, 2019.

[20] Deschaintre V, Aittala M, Durand F, et al. Single-image svbrdf capture with a rendering-aware deep network[J]. ACM Transactions on Graphics (ToG), 2018, 37(4): 1-15.

[21] Li Z., Sunkavali K., Chandraker M.: Materials for masses: Svbrdf acquisition with a single mobile phone image. In ECCV (2018), pp. 72–87.

[22]Eslami S M A, Jimenez Rezende D, Besse F, et al. Neural scene representation and rendering[J]. Science, 2018, 360(6394): 1204-1210.

[23] Goodfellow I, Pouget-Abadie J, Mirza M, et al. Generative adversarial nets[J]. Advances in neural information processing systems, 2014, 27.

[24] Radford A, Metz L, Chintala S. Unsupervised representation learning with deep convolutional generative adversarial networks[J]. arXiv preprint arXiv:1511.06434, 2015.

[25] Karras T, Aila T, Laine S, et al. Progressive growing of gans for improved quality, stability, and variation[J]. arXiv preprint arXiv:1710.10196, 2017.

[26] Brock A, Donahue J, Simonyan K. Large scale GAN training for high fidelity natural image synthesis[J]. arXiv preprint arXiv:1809.11096, 2018.

[27] Vondrick C, Pirsiavash H, Torralba A. Generating videos with scene dynamics[J]. Advances in neural information processing systems, 2016, 29.

[28] Clark A, Donahue J, Simonyan K. Efficient video generation on complex datasets[J]. 2019.

[29] Karras T, Laine S, Aila T. A style-based generator architecture for generative adversarial networks[C]//Proceedings of the IEEE/CVF conference on computer vision and pattern recognition. 2019: 4401-4410.

[30] Barnes C, Shechtman E, Finkelstein A, et al. PatchMatch: A randomized correspondence algorithm for structural image editing[J]. ACM Trans. Graph., 2009, 28(3): 24.

[31] Dosovitskiy A, Tobias Springenberg J, Brox T. Learning to generate chairs with convolutional neural networks[C]// Proceedings of the IEEE conference on computer vision and pattern recognition. 2015: 1538-1546.

[32] Isola P, Zhu J Y, Zhou T, et al. Image-to-image translation with conditional adversarial networks[C]//Proceedings of the IEEE conference on computer vision and pattern recognition. 2017: 1125-1134.

[33] Blau Y, Michaeli T. The perception-distortion tradeoff[C]//Proceedings of the IEEE conference on computer vision and pattern recognition. 2018: 6228-6237.

[34] Gatys L A, Ecker A S, Bethge M. Image style transfer using convolutional neural networks[C]//Proceedings of the IEEE conference on computer vision and pattern recognition. 2016: 2414-2423.

[35] Dosovitskiy A, Brox T. Generating images with perceptual similarity metrics based on deep networks[J]. Advances in neural information processing systems, 2016, 29.

[36] Johnson J, Alahi A, Fei-Fei L. Perceptual losses for real-time style transfer and super-resolution[C]//European conference on computer vision. Springer, Cham, 2016: 694-711.

[37] Ledig C, Theis L, Huszár F, et al. Photo-realistic single image super-resolution using a generative adversarial network [C]//Proceedings of the IEEE conference on computer vision and pattern recognition. 2017: 4681-4690.

[38] Mirza M, Osindero S. Conditional generative adversarial nets[J]. arXiv preprint arXiv:1411.1784, 2014.

[39] Kajiya J T. The rendering equation[C]//Proceedings of the 13th annual conference on Computer graphics and interactive techniques. 1986: 143-150.

[40] Mescheder L, Oechsle M, Niemeyer M, et al. Occupancy networks: Learning 3d reconstruction in function space [C]//Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. 2019: 4460-4470.

[41] Chen Z, Zhang H. Learning implicit fields for generative shape modeling[C]//Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. 2019: 5939-5948.

[42] Park J J, Florence P, Straub J, et al. Deepsdf: Learning continuous signed distance functions for shape representation [C]//Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. 2019: 165-174.

[43] Saito S, Huang Z, Natsume R, et al. Pifu: Pixel-aligned implicit function for high-resolution clothed human digitization [C]//Proceedings of the IEEE/CVF International Conference on Computer Vision. 2019: 2304-2314.

[44] Genova K, Cole F, Vlasic D, et al. Learning shape templates with structured implicit functions[C]//Proceedings of the IEEE/CVF International Conference on Computer Vision. 2019: 7154-7164.

[45] Deng B, Genova K, Yazdani S, et al. Cvxnet: Learnable convex decomposition[C]//Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. 2020: 31-44.

[46] Yariv L, Atzmon M, Lipman Y. Universal differentiable renderer for implicit neural representations[J]. 2020.

[47] Lombardi S, Simon T, Saragih J, et al. Neural volumes: Learning dynamic renderable volumes from images[J]. arXiv preprint arXiv:1906.07751, 2019.

[48] Mildenhall B, Srinivasan P P, Tancik M, et al. Nerf: Representing scenes as neural radiance fields for view synthesis [C]//European conference on computer vision. Springer, Cham, 2020: 405-421.

[49] Schonberger J L, Frahm J M. Structure-from-motion revisited[C]//Proceedings of the IEEE conference on computer vision and pattern recognition. 2016: 4104-4113.

[50] Schwarz K, Liao Y, Niemeyer M, et al. Graf: Generative radiance fields for 3d-aware image synthesis[J]. Advances in Neural Information Processing Systems, 2020, 33: 20154-20166.

[51] Henzler P, Mitra N J, Ritschel T. Escaping Plato’s cave: 3D shape from adversarial rendering[C]//Proceedings of the IEEE/CVF International Conference on Computer Vision. 2019: 9984-9993.

[52] Nguyen-Phuoc T, Li C, Theis L, et al. Hologan: Unsupervised learning of 3d representations from natural images [C]//Proceedings of the IEEE/CVF International Conference on Computer Vision. 2019: 7588-7597.

[53] Niemeyer M, Geiger A. Giraffe: Representing scenes as compositional generative neural feature fields[C]//Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. 2021: 11453-11464.

---

1. 1 ↩︎

2. 2 ↩︎

3. 3 ↩︎

4. 4 ↩︎

5. 5 ↩︎

6. 6 ↩︎

7. 7 ↩︎

8. 8 ↩︎

9. 9 ↩︎

10. 10 ↩︎

11. 11 ↩︎

12. 12 ↩︎

13. 14 ↩︎

14. 15 ↩︎

15. 16 ↩︎

16. 17 ↩︎

17. 18 ↩︎

18. 19 ↩︎

19. 20 ↩︎

20. 21 ↩︎

21. 39 ↩︎

22. 22 ↩︎

23. 23 ↩︎

24. 24 ↩︎

25. 25 ↩︎

26. 26 ↩︎

27. 27 ↩︎

28. 28 ↩︎

29. 29 ↩︎

30. 30 ↩︎

31. 38 ↩︎

32. 31 ↩︎

33. 32 ↩︎

34. 33 ↩︎

35. 34 ↩︎

36. 35 ↩︎

37. 36 ↩︎

38. 34 ↩︎

39. 36 ↩︎

40. 35 ↩︎

41. 36 ↩︎

42. 37 ↩︎

43. 40 ↩︎

44. 41 ↩︎

45. 42 ↩︎

46. 43 ↩︎

47. 44 ↩︎

48. 45 ↩︎

49. 46 ↩︎

50. 42 ↩︎

51. 48 ↩︎

52. 47 ↩︎

53. 49 ↩︎

54. 50 ↩︎

55. 51 ↩︎

56. 52 ↩︎

57. 53 ↩︎