Boosting方法及代码实战

1. Boosting基本思路

  Boosting（提升）方法是一种常用的统计学习方法，应用广泛且有效，在分类问题中，它通过改变训练样本的权重，学习多个分类器，并将这些分类器进行线性组合，提高分类的性能。它是不断的重复学习以达到最终的要求。
  Boosting中有"强可学习"和"弱可学习"两个概念。在概率近似正确PAC学习的框架下:

• 弱学习：识别错误率小于1/2（即准确率仅比随机猜测略高的学习算法）
• 强学习：识别准确率很高并能在多项式时间内完成的学习算法

  对于Boosting方法来说，有两个问题需要给出答案：第一个是每一轮学习应该如何改变数据的概率分布，第二个是如何将各个弱分类器组合起来。关于这两个问题，不同的Boosting算法会有不同的答案，我们接下来介绍一种最经典的Boosting算法----Adaboost。

2. Adaboost算法的简单介绍

  对于Adaboost来说，解决上述的两个问题的方式是：**1. 提高那些被前一轮分类器错误分类的样本的权重，而降低那些被正确分类的样本的权重。**这样一来，那些在上一轮分类器中没有得到正确分类的样本，由于其权重的增大而在后一轮的训练中“备受关注”。2. 各个弱分类器的组合是通过采取加权多数表决的方式，具体来说，加大分类错误率低的弱分类器的权重，因为这些分类器能更好地完成分类任务，而减小分类错误率较大的弱分类器的权重，使其在表决中起较小的作用。 （具体原理部分推荐李航老师的《统计学习方法》）

3. 代码实践

  我们通过使用UCI的机器学习库里的开源数据集：葡萄酒数据集（下载地址：
https://archive.ics.uci.edu/ml/machine-learning-databases/wine/wine.data）。该数据集包括了有178个样本和13个特征，我们要根据这些数据预测红酒属于哪一个类别。

#导入第三方库
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
plt.style.use('ggplot')
%matplotlib inline
import seaborn as sns

#读取数据集
wine = pd.read_csv("wine.data",header=None)
#查看前五行数据
wine.head()

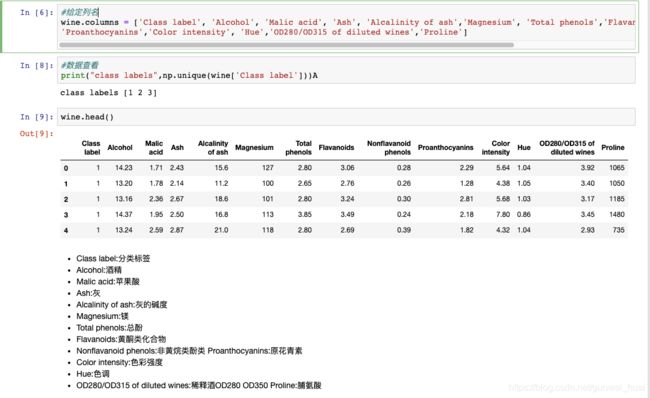
#给定列名
wine.columns = ['Class label', 'Alcohol', 'Malic acid', 'Ash', 'Alcalinity of ash','Magnesium', 'Total phenols','Flavanoids', 'Nonflavanoid phenols',
'Proanthocyanins','Color intensity', 'Hue','OD280/OD315 of diluted wines','Proline']
#类别数据数据查看
print("class labels",np.unique(wine['Class label']))
wine.head() #查看此时数据格式

# 数据预处理
# 仅仅考虑2，3类葡萄酒，去除1类
wine = wine[wine['Class label']!= 1]
y = wine['Class label'].values #种类标签
X = wine[['Alcohol','OD280/OD315 of diluted wines']].values #酒精含量和稀释酒

# 将分类标签变成二进制编码(当标签是两类的时候可以直接使用二进制编码)
from sklearn.preprocessing import LabelEncoder
le = LabelEncoder()
y = le.fit_transform(y)
print(y)
print( wine['Class label'].values)

# 按8：2分割训练集和测试集
from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.2,random_state=1,stratify=y)  # stratify参数代表了按照y的类别等比例抽样

# 使用单一决策树建模
from sklearn.tree import DecisionTreeClassifier
tree = DecisionTreeClassifier(criterion='entropy',random_state=1,max_depth=1)
from sklearn.metrics import accuracy_score
tree = tree.fit(X_train,y_train)
y_train_pred = tree.predict(X_train)
y_test_pred = tree.predict(X_test)
tree_train = accuracy_score(y_train,y_train_pred)
tree_test = accuracy_score(y_test,y_test_pred)
print('Decision tree train/test accuracies %.3f/%.3f' % (tree_train,tree_test))

# 使用sklearn实现Adaboost(基分类器为决策树)
'''
AdaBoostClassifier相关参数：
base_estimator：基本分类器，默认为DecisionTreeClassifier(max_depth=1)
n_estimators：终止迭代的次数
learning_rate：学习率
algorithm：训练的相关算法，{'SAMME'，'SAMME.R'}，默认='SAMME.R'
random_state：随机种子
'''
from sklearn.ensemble import AdaBoostClassifier
ada = AdaBoostClassifier(base_estimator=tree,n_estimators=500,learning_rate=0.1,random_state=1)
ada = ada.fit(X_train,y_train)
y_train_pred = ada.predict(X_train)
y_test_pred = ada.predict(X_test)
ada_train = accuracy_score(y_train,y_train_pred)
ada_test = accuracy_score(y_test,y_test_pred)
print('Adaboost train/test accuracies %.3f/%.3f' % (ada_train,ada_test))

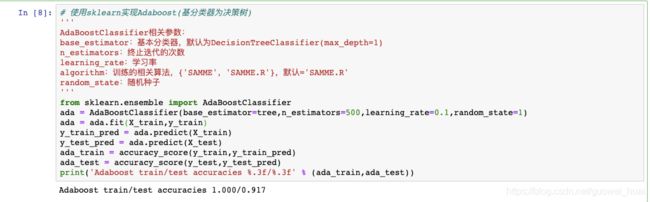
  我们发现，单层的决策树对训练数据欠拟合，而Adaboost模型正确地预测了训练训练的所有分类标签，而且单层决策树相比，Adaboost的测试性能也提高了。下面我们通过代码生成图像来说明为什么它们在训练集和测试集的性能相差这么大：

# 画出单层决策树与Adaboost的决策边界：
x_min = X_train[:, 0].min() - 1
x_max = X_train[:, 0].max() + 1
y_min = X_train[:, 1].min() - 1
y_max = X_train[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.1),np.arange(y_min, y_max, 0.1))
f, axarr = plt.subplots(nrows=1, ncols=2,sharex='col',sharey='row',figsize=(12, 6))
for idx, clf, tt in zip([0, 1],[tree, ada],['Decision tree', 'Adaboost']):
    clf.fit(X_train, y_train)
    Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
    Z = Z.reshape(xx.shape)
    axarr[idx].contourf(xx, yy, Z, alpha=0.3)
    axarr[idx].scatter(X_train[y_train==0, 0],X_train[y_train==0, 1],c='blue', marker='^')
    axarr[idx].scatter(X_train[y_train==1, 0],X_train[y_train==1, 1],c='red', marker='o')
    axarr[idx].set_title(tt)
axarr[0].set_ylabel('Alcohol', fontsize=12)
plt.tight_layout()
plt.text(0, -0.2,s='OD280/OD315 of diluted wines',ha='center',va='center',fontsize=12,transform=axarr[1].transAxes)
plt.show()

  从上图的决策边界图，我们能够知道：Adaboost的决策边界比单层决策树的决策边界要复杂的多。换句话说，Adaboost方法在试图通过增加模型复杂度来降低偏差，从而减少总误差。但是在这个过程中引入了方差，也可能会出现过拟合，因此在训练集和测试集之间的性能存在较大的差异。

4. 总结

  虽然与单个分类器相比较，Adaboost等Boosting方法可以提高性能，但是它们也增加了计算的复杂度，在实践中需要仔细思考是否值得去为预测性能的相对改善而增加计算成本，而且Boosting方法也是无法做到现在流行的并行计算方法（因为每一步的跌倒都需要基于上一步的基本分类器）。后面我会介绍更多的集成学习方法～