差分隐私与机器学习

注意事项

1. 文章原文：How to deploy machine learning with differential privacy
2. 要求需要有一定的机器学习、差分隐私基础
3. 差分隐私基础知识
4. 文章介绍了机器学习引入差分隐私的原因，以及如何在机器学习中部署带有差分隐私的实例和部署的困难，文章最后介绍了本文没有涵盖到的差分隐私领域
5. 如果对联邦学习和差分隐私感兴趣，请点击 联邦学习与差分隐私
6. 如果想了解联邦学习是什么可以看这几篇论文：
   Communication-Efficient Learning of Deep Networks from Decentralized Data
   Federated Machine Learning: Concept and Applications

如何部署具有差异隐私的机器学习？

在机器学习的许多应用中，例如用于医学诊断的机器学习，我们希望机器学习算法不记住有关训练集的敏感信息，例如个体患者的特定病史。差分隐私是一个概念，它允许量化算法在其运行的底层（敏感）数据集上提供隐私保护程度。通过差分隐私的视角，我们可以设计机器学习算法以至于在私有数据上负责任地训练模型。

为什么我们需要私有机器学习算法？

机器学习算法的工作原理是研究大量数据并更新其参数以编码该数据中的关系。理想情况下，我们希望这些机器学习模型的参数能够编码一般模式（例如，“吸烟的患者更容易患心脏病”），而不是关于特定训练示例的事实（例如，“Jane Smith患有心脏病”）。不幸的是，机器学习算法不会学会默认忽略这些细节。如果我们想使用机器学习来解决一项重要任务，比如制作癌症诊断模型，那么当我们发布机器学习模型时（例如，通过制作一个开源的癌症诊断模型供世界各地的医生使用），我们也可能无意中透露了有关训练集的信息。恶意攻击者可能能够检查已发布模型的预测并了解有关 Jane Smith 的私人信息。例如，攻击者可以发起成员资格推理攻击，以了解 Jane Smith 是否将她的数据贡献给了模型的训练集 [SSS17]。攻击者还可以基于成员推断攻击，通过反复猜测可能的训练点来提取训练数据，直到它们从模型的预测中产生足够强的成员信号[CTW20]。在许多情况下，模型本身可能由一些数据样本表示（例如，其对偶形式的支持向量机）。

一个常见的误解是，如果模型泛化（即，在测试示例上表现良好），那么它保护了隐私。如前所述，这远非事实。其中一个主要原因是泛化是模型的平均情况行为（在数据样本的分布上），因此必须为每个人提供隐私，包括异常值（这可能偏离我们的分布假设）。

多年来，研究人员提出了各种方法来保护学习算法中的隐私（k-anonymity [SS98]，l-diversity [MKG07]，m-invariance [XT07]，t-closeness [LLV07]等）。不幸的是，[GKS08]所有这些方法都容易受到所谓的组合攻击，这些攻击使用辅助信息来破坏隐私保护。众所周知，当个人也在互联网电影数据库 (IMDb)[NS08] 上公开分享他们的电影评分时，该策略允许研究人员对发布给 Netflix 奖参与者的电影评分数据集的一部分进行去匿名化处理 。如果简·史密斯（Jane Smith）在Netflix Prize数据集中为电影A，B和C分配了相同的评级，并在相似的时间在IMDb上公开，那么研究人员可以在两个数据集中链接与Jane对应的数据。这反过来又会为他们提供恢复Netflix奖中包括的收视率的方法，而不是在IMDb上。这个例子表明，定义和保证隐私是多么困难，因为很难估计对手可以获得的关于个人的知识范围。虽然Netflix发布的数据集已被删除，但很难确保其所有副本都已被删除。近年来，基于数据样本实例编码的方法，如InstaHide [HSL20]和NeuraCrypt [YEO21]也被证明容易受到这种组合攻击。

因此，研究界已经趋同于差分隐私[DMNS06]，它提供了以下语义保证，而不是临时方法：对手学习关于个人的几乎相同的信息，无论他们是否存在于训练数据集中。特别是，它提供了算法的条件，与可能攻击它的人或数据集实例化的细节无关。换句话说，差分隐私是一个框架，用于评估旨在保护隐私的系统提供的保证。此类系统可以直接应用于可能仍包含敏感信息的"原始"数据，完全消除了对数据进行清理或匿名化处理的程序的需求，并且容易出现上述故障。也就是说，首先尽量减少数据收集仍然是限制其他形式的隐私风险的良好做法。

通过差分隐私设计私有机器学习算法

差分隐私 [DMNS06] 是隐私的一个语义概念，它解决了以前方法（如 k-anonymity）的许多局限性。基本思想是随机化部分机制的行为以提供隐私。在我们的例子中，所考虑的机制是一种学习算法，但差分隐私框架可以应用于研究任何算法。

我们为什么要在学习算法中引入随机性的直觉是，它掩盖了个人的贡献，但并没有掩盖重要的统计模式。如果没有随机性，我们将能够提出这样的问题："当我们在这个特定的数据集上训练学习算法时，它会选择哪些参数？对于学习算法中的随机性，我们反而会问这样的问题："当我们在这个特定的数据集上训练它时，学习算法在这组可能的参数中选择参数的概率是多少？

我们使用一个差分隐私版本，它要求（在我们的机器学习用例中）如果我们更改训练集中的单个数据记录，则学习任何特定参数集的概率大致相同。数据记录可以是来自个人的单个训练示例，也可以是个人提供的所有训练示例的集合。前者通常称为示例级别/项目级别隐私，后者称为用户级别差分隐私。虽然用户级隐私提供了更强的语义，但可能更难实现。有关这些概念的分类的更全面的讨论，请参阅[DNPR10，JTT18，HR12，HR13]。在本文档中，为了便于阐述技术结果，我们将重点放在示例级别概念上。这可能意味着添加训练示例、删除训练示例或更改一个训练示例中的值。直觉是，如果一个病人（简·史密斯）对学习的结果没有多大影响，那么这个病人的记录就无法被记住，她的隐私也会得到尊重。在本文的其余部分中，单个记录对学习结果的影响程度称为算法的灵敏度。

差分隐私的保证是，对手无法区分基于三个用户中的两个数据随机算法产生的答案与基于所有三个用户数据的相同算法返回的答案。我们还将不可区分的程度称为隐私损失。较小的隐私损失对应于更强的隐私保证。

人们通常认为，隐私是获得机器学习算法的良好预测准确性/泛化的根本瓶颈。事实上，最近的研究表明，在许多情况下，它实际上有助于设计具有强大泛化能力的算法。DP导致设计更好的学习算法的一些例子是在线线性预测[KV05]和在线PCA [DTTZ13]。值得注意的是，[DFH15]正式表明，任何DP学习算法的泛化都是免费的。更具体地说，如果DP学习算法具有良好的训练精度，则可以保证具有良好的测试精度。这是真的，因为差分隐私本身就是一种非常强大的正则化形式。

有人可能会争辩说，DP算法可以实现的泛化保证可能低于其非私有基线。对于一大类学习任务，可以证明渐近DP除了固有的统计误差[SSTT21]之外不会引入任何进一步的误差。[ACG16，BFTT19]强调，在存在足够数据的情况下，DP算法可以任意接近固有的统计误差，即使在强隐私参数下也是如此。

私人经验风险最小化

在我们进入特定差分私有学习算法的设计之前，我们首先将问题设置形式化，并标准化一些符号。考虑训练数据集D=(x1,y1)……（xn,yn）提取 i.i.d。从某些固定（未知）分布中∏, 确定特征向量为xn和标签yn。我们定义任何模型 θ 的训练损失为：

相应的测试损失为：

我们将设计DP算法来输出模型，这些模型可以最大限度地减少测试损失，同时只能访问训练损失。

在文献中，有多种方法可以设计这些DP学习算法[CMS11，KST12，BST14，PAE16，BTT18]。研究者可以将它们大致分类为：

1. 假设单个损失函数 l(θ; ·) 的算法在模型参数中凸起以确保差分隐私，
2. 即使损失函数本质上是非凸的，算法也是差分私有的（例如，深度学习模型）
3. 模型不可知的算法，不需要关于模型 θ 的表示或损失函数l(θ; ·)的任何信息

在我们目前的讨论中，我们将只专注于为 (2) 和 (3) 设计算法。 这是因为事实证明（2）的最知名算法已经与特定于（1）的算法产生了竞争

用于训练深度学习模型的私有算法

由于 SCS13、BST14 和 ACG16，所以第一种方法被命名为 微分私有随机梯度下降 （DP-SGD）。它建议修改深度学习中最常用的优化器计算模型的更新：随机梯度下降（SGD）。

DP-SGD

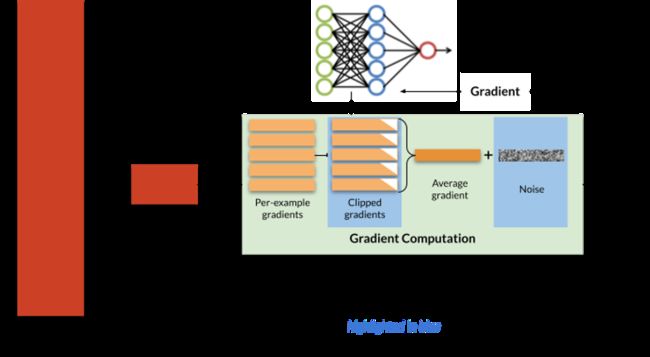
图一：随机梯度下降 (SGD) 和差分私有 SGD (DP-SGD)。 为了实现差分隐私，在更新模型参数之前，DP-SGD 对梯度进行剪辑并添加噪声，基于每个示例计算。 DP-SGD 所需的步骤以蓝色突出显示； 非私有 SGD 省略了这些步骤。
DP-SGD算法来源 可以查看文章：Deep Learning with Differential Privacy

通常，随机梯度下降以迭代方式训练。在每次迭代中，都会从训练集中抽取少量训练示例（“小批次”）。优化程序计算这些示例的平均模型误差，然后根据每个模型参数区分此平均误差，以获得梯度向量。最后，模型参数: (${\theta }_t$) 通过减去此梯度:（${\nabla }_t$） 乘以一个小常量：$\eta$（学习速率控制优化程序更新模型参数的速度）。

在较高层次上，DP-SGD进行了两项修改以获得差分隐私：梯度是按每个示例计算的（而不是在多个示例中平均），首先被裁剪以控制其灵敏度, 其次，球面高斯噪声 $b_t$ 添加到它们的总和中以获得DP所需的不可区分性。简言之，更新步骤可以编写如下：
$${\nabla }_{t+1}\leftarrow {\theta }_t-\eta \cdot ({\nabla }_t+b_t)$$
让我们以医院训练模型的例子来预测患者在出院后是否会再次入院。为了训练模型，医院使用来自患者记录的信息，例如人口统计变量和入院变量（例如，年龄，种族，保险类型，重症监护病房的类型），以及随时间变化的生命体征和实验室（例如，心率，血压，白细胞计数）[JPS16]。DP-SGD所做的修改确保几个方面（1）如果Jane Smith的个人患者记录包含异常特征，例如，她的保险提供商对她这个年龄的人来说不常见，或者她的心率遵循不寻常的模式，则产生的信号将对我们的模型更新产生有限影响。（2）如果 Jane Smith 选择不向训练集贡献（即选择退出）她的患者记录，则模型的最终参数将基本相同。当一个人能够引入更多噪声（即具有更大标准偏差的样本噪声）并训练尽可能少的迭代时，可以实现更强的差分隐私。

上述DP-SGD算法与传统SGD不同的两个主要组成部分是：

1. 每个实例都要进行剪切
2. 高斯噪声加法。

此外，为了保持分析，DP-SGD 要求从训练数据集中随机对迷你批次进行均匀抽样。虽然这不是DP-SGD本身的要求，但在实践中，SGD的许多实现并不满足这一要求，而是在每个训练时期分析数据的不同排列。

虽然梯度剪切在深度学习中很常见，通常用作正则化的一种形式，但它与DP-SGD不同如以下所示：对小批量的平均梯度进行裁剪，而不是在平均之前裁剪单个示例的梯度（即 $l({\theta }_t;(x,y)$ )。这是一个持续的研究方向，既要了解模型训练中 DP-SGD 中每个示例裁剪的效果[SSTT21]，也要了解其在准确性[PTS21]和训练时间[ZHS19]方面减轻其影响的有效方法。

在标准随机梯度下降中，子采样通常用作加速训练过程的一种方式[CAR16]，或作为正则化[RCR15]的一种形式。在DP-SGD中，小批量子采样中的随机性用于保证 DP。这种隐私分析的技术组成称为通过子采样进行隐私放大[KLNRS08，BBG18]。由于采样随机性用于保证DP，因此采样步骤中的均匀性具有加密强度显得至关重要。DP-SGD的另一个（可能）违反直觉的特征是，为了获得最佳的隐私/实用性权衡，通常最好采用具有更大的批量。事实上，全批次 DP-梯度下降可能提供最好的隐私

对于固定的DP保证，在 DP-SGD 的每个步骤中添加到梯度更新中的高斯噪声的大小与训练模型的 $\sqrt{thenumberofsteps}$ 成正比。因此，调整训练步骤的数量以获得最佳隐私/实用性权衡非常重要。

在下面的教程中，我们提供了一个小代码段来训练使用 DP-SGD 训练模型。

Model agnostic private learning（模型不可知的私人学习）

DP-SGD 在模型训练期间向梯度添加噪声，这会损害准确性。 我们能做得更好吗？ Model agnostic private learning 采用了不同的方法，并且在某些情况下，与 DP-SGD 相比，在相同隐私级别上实现了更好的准确性。

Model agnostic private learning 利用了样本和聚合框架 [NRS07]，这是一种在不关心其内部工作的情况下向非私有算法添加差异隐私的通用方法，即模型不可知。在机器学习的背景下，可以这样陈述主要思想：考虑一个多类分类问题。获取训练数据，并拆分为大小相等的 k 个不相交子集。在不相交的子集上训练独立模型${\theta }_1\theta 2\dots \dots {\theta }_k$。为了在测试示例 x 上进行预测，首先，在 k 个预测集 ${\theta }_1(x),{\theta }_2(x)\dots \dots {\theta }_k(x)$ 上计算一个私有直方图。然后，在将少量 拉普拉斯/高斯噪声 添加到计数后，根据最高计数选择并输出直方图中的箱。在DP学习的背景下，这种特殊的方法被用于两个不同的工作领域：i）PATE [PAE16] 和 ii）模型不可知论的私人学习[BTT18]。而后者专注于为一类学习任务获得理论上的隐私/效用权衡(例如：agnostic PAC learning)，但 PATE 方法侧重于实际部署。这两条工作路线都有一个共同的观察。如果来自 ${\theta }_1(x),{\theta }_2(x)\dots \dots {\theta }_k(x)$ 预测都相当一致，那么就DP而言，隐私成本非常小。因此，可以运行大量预测查询，而不会违反 DP 约束。在下文中，我们将详细描述PATE方法。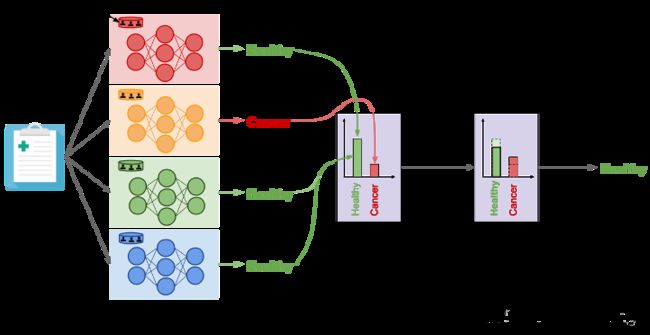
PATE 框架。 PATE 不是在梯度中添加噪声，而是在数据子集上训练许多非私有模型（“教师”），然后要求模型使用差分私有聚合机制对正确的预测“投票”。
该方法来自与论文：Semi-supervised Knowledge Transfer for Deep Learning from Private Training Data

教师融合（PATE）的私有聚合特别表明，这种方法允许人们学习具有微分隐私的深度神经网络。它建议通过让这些模型进行聚合预测而不是揭示其个人预测，在没有隐私的情况下训练模型，并使用差分隐私进行预测。在 PATE 中，我们首先将私有数据集划分为较小的数据子集。这些子集是分区，因此任何分区对中包含的数据之间没有重叠。如果 Jane Smith 的记录位于我们的私有数据集中，则它仅包含在其中一个分区中。也就是说，只有一位老师在培训期间分析了简·史密斯的记录。我们在每个分区上训练一个 ML 模型（称为教师）。我们现在有一套教师模型，这些模型是独立训练的，但没有任何隐私保证。我们如何利用这个融合来做出尊重隐私的预测？在 PATE 中，我们添加噪声，同时聚合每个教师单独做出的预测，以形成一个单一的通用预测。我们计算每个班级投票的教师人数，然后通过添加从拉普拉斯或高斯分布中抽样的随机噪声来扰动该计数。噪声聚合机制预测的每个标签都附带严格的差分隐私保证，这些保证将花费的隐私预算绑定到标记该输入上。同样，当我们能够在聚合中引入更多噪声并能够回答尽可能少的查询时，可以实现更强的差异隐私。现在让我们回到运行示例。想象一下，我们想使用PATE的输出来了解Jane是否喜欢某部电影。唯一一位在包含简·史密斯数据的分区上接受过培训的老师现在已经了解到，与简相似的记录是喜欢类似电影的个人的特征，因此，在类似于简的测试输入上更改其预测，以预测简分配的电影评级。但是，由于教师只对聚合贡献了一票，并且聚合注入了噪声，因此我们无法知道教师是否将其预测更改为 Jane 分配的电影评级，因为教师确实根据 Jane 的数据进行了训练，或者因为在聚合过程中注入的噪声"翻转"了该教师的投票。添加到投票计数中的随机噪声会阻止聚合结果反映任何单个教师的投票，以保护隐私。

在机器学习中实际部署差分隐私

我们介绍的两种方法的优点是概念上易于理解。幸运的是，这些方法也存在几种开源实现。例如，DP-SGD在TensorFlow Privacy，Objax和Opacus中实现。这意味着人们能够采用现有的TensorFlow，JAX或PyTorch管道来训练机器学习模型，并将非私有优化器替换为DP-SGD。PATE的示例实现也可以在TensorFlow Privacy中找到。那么，部署具有差异隐私的机器学习的具体潜在障碍是什么？

第一个障碍是隐私保护模型的准确性。数据集通常从长尾分布中采样的。例如，在医疗应用中，具有特定医疗状况的患者通常（幸运的是）比没有该病症的患者少。这意味着对于患有每种疾病的患者来说，可以学习的培训示例较少。因为差分隐私阻止我们学习在训练数据中通常找不到的模式，所以它限制了我们从这些患者身上学习的能力，而我们很少有SPG的例子。更一般地说，模型的准确性和训练它所采用的差分隐私保证的强度之间通常存在权衡：隐私预算越小，对准确性的影响通常越大。也就是说，这种紧张关系并不总是不可避免的，在某些情况下，隐私和准确性是协同的，因为差分隐私意味着泛化[DFH15]（但反之亦然）。

第二个障碍可能是计算开销。例如，在DP-SGD中，必须计算每个示例的梯度，而不是平均梯度。这通常意味着在机器学习框架中实现的优化以利用底层硬件加速器（例如 GPU）支持的矩阵代数更难利用。在另一个例子中，PATE要求一个训练多个模型（教师）而不是单个模型，因此这也会在训练过程中引入开销。幸运的是，这种成本在最近的私有学习算法的实现中得到了很大的缓解，特别是在Objax和Opacus中。

在机器学习中但更普遍地在任何形式的数据分析中，部署差异隐私的第三个障碍是隐私预算的选择。预算越小，保证越强。这意味着人们可以比较两种分析，并说出哪一种是"更私密的"。然而，这也意味着目前尚不清楚隐私预算的"足够小"。这尤其成问题，因为将差分隐私应用于机器学习通常需要提供很少理论保证的隐私预算，以便训练一个准确度足够大以保证有用部署的模型。因此，对于从业者来说，通过自己攻击机器学习算法来评估其机器学习算法的隐私可能会很有趣。虽然对算法的差异隐私保证的理论分析提供了最坏情况的保证，限制了算法可以针对任何对手泄漏多少私人信息，但实施特定攻击对于了解特定对手或对手类别的成功程度很有用。这有助于解释理论保证，但不能被视为直接替代它。此类攻击的开源实现越来越多：例如，在这里和这里进行成员资格推断。

结论

在上面，我们讨论了一些用于微分私有模型训练的算法方法，这些方法在理论和实践环境中都是有效的。由于这是一个快速增长的领域，我们无法涵盖研究领域的所有重要方面。一些突出的包括：
1：在DP模型训练中选择最佳超参数。为了确保整体算法保留差分隐私，一个需求就是确保超参数本身保留DP。最近的研究提供了以差分私有方式选择最佳超参数的算法[LT19]。
2：网络架构的选择：用于非私有模型训练的最知名的模型架构确实最适合具有微分隐私的训练，这并不总是正确的。特别是，我们知道模型参数的数量可能会对隐私/效用权衡产生不利影响[BST14]。因此，选择正确的模型体系结构对于提供良好的隐私/实用性权衡非常重要 [PTS21]。
3：在联合/分布式设置中进行训练：在上面的阐述中，我们假设训练数据位于单个集中位置。但是，在联邦学习（FL）[MMRHA17]设置中，数据记录可以高度分布，例如，在各种移动设备之间。在 FL 设置中运行 DP-SGD，这是 FL 为训练数据提供隐私保证所必需的，它提出了一系列挑战 [KMA19]，这些挑战通常由专为 FL 设置设计的分布式私有学习算法 [BKMTT20，KMSTTZ21] 来促进。FL 背景下的一些具体挑战包括，有限且不统一的客户端可用性（持有个人数据记录）以及训练数据的未知（和可变）大小[BKMTT18]。另一方面，PATE 风格的算法一旦与现有的密码原语相结合，就会自然地适用于分布式设置，如 CaPC 协议 [CDD21] 所示。这是一个活跃的研究领域，以应对上述挑战。

致谢

The authors would like to thank Thomas Steinke and Andreas Terzis for detailed feedback and edit suggestions. Parts of this blog post previously appeared on www.cleverhans.io.

引用

[ACG16] Abadi, M., Chu, A., Goodfellow, I., McMahan, H. B., Mironov, I., Talwar, K., & Zhang, L. (2016, October). Deep learning with differential privacy. In Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security (pp. 308-318). ACM.

[BBG18] Balle, B., Barthe, G., & Gaboardi, M. (2018). Privacy amplification by subsampling: Tight analyses via couplings and divergences. arXiv preprint arXiv:1807.01647.

[BKMTT18] Balle, B., Kairouz P., McMahan M., Thakkar O. & Thakurta A. (2020). Privacy amplification via random check-ins. In NeurIPS.

[MMRHA17] McMahan, B., Moore, E., Ramage, D., Hampson, S., & y Arcas, B. A. (2017, April). Communication-efficient learning of deep networks from decentralized data. In Artificial intelligence and statistics (pp. 1273-1282). PMLR.

[KMSTTZ18] Kairouz P., McMahan M., Song S., Thakkar O., Thakurta A., & Xu Z. (2021). Practical and Private (Deep) Learning without Sampling or Shuffling. In ICML.

[BFTT19] Bassily, R., Feldman, V., Talwar, K., & Thakurta, A. Private Stochastic Convex Optimization with Optimal Rates. In NeurIPS 2019.

[BST14] Raef Bassily, Adam Smith, and Abhradeep Thakurta. Private empirical risk minimization: Efficient algorithms and tight error bounds. In Proceedings of the 55th Annual IEEE Symposium on Foundations of Computer Science.

[BTT18] Bassily, R., Thakurta, A. G., & Thakkar, O. D. (2018). Model-agnostic private learning. Advances in Neural Information Processing Systems.

[CDD21] Choquette-Choo, C. A., Dullerud, N., Dziedzic, A., Zhang, Y., Jha, S., Papernot, N., & Wang, X. (2021). CaPC Learning: Confidential and Private Collaborative Learning. arXiv preprint arXiv:2102.05188.

[CMS11] Chaudhuri, K., Monteleoni, C., & Sarwate, A. D. (2011). Differentially private empirical risk minimization. Journal of Machine Learning Research, 12(3).

[CTW20] Carlini, N., Tramer, F., Wallace, E., Jagielski, M., Herbert-Voss, A., Lee, K., … & Raffel, C. (2020). Extracting training data from large language models. arXiv preprint arXiv:2012.07805.

[DFH15] Dwork, C., Feldman, V., Hardt, M., Pitassi, T., Reingold, O., & Roth, A. (2015). Generalization in adaptive data analysis and holdout reuse. arXiv preprint arXiv:1506.02629.

[DMNS06] Dwork, C., McSherry, F., Nissim, K., & Smith, A. (2006, March). Calibrating noise to sensitivity in private data analysis. In Theory of Cryptography Conference (pp. 265-284). Springer, Berlin, Heidelberg.

[DNPR10] Dwork, C., Naor, M., Pitassi, T., & Rothblum, G. N. (2010, June). Differential privacy under continual observation. In Proceedings of the forty-second ACM symposium on Theory of computing (pp. 715-724).

[DTTZ14] Dwork, C., Talwar, K., Thakurta, A., & Zhang, L. (2014, May). Analyze gauss: optimal bounds for privacy-preserving principal component analysis. In Proceedings of the forty-sixth annual ACM symposium on Theory of computing (pp. 11-20).

[HSL20] Huang, Y., Song, Z., Li, K., & Arora, S. (2020, November). Instahide: Instance-hiding schemes for private distributed learning. In International Conference on Machine Learning (pp. 4507-4518). PMLR.

[HR12] Hardt, M., & Roth, A. (2012, May). Beating randomized response on incoherent matrices. In Proceedings of the forty-fourth annual ACM symposium on Theory of computing (pp. 1255-1268).

[HR13] Hardt, M., & Roth, A. (2013, June). Beyond worst-case analysis in private singular vector computation. In Proceedings of the forty-fifth annual ACM symposium on Theory of computing (pp. 331-340).

[JPS16] Johnson, A., Pollard, T., Shen, L. et al. MIMIC-III, a freely accessible critical care database. Sci Data 3, 160035 (2016). https://doi.org/10.1038/sdata.2016.35

[JTT18] Jain, P., Thakkar, O. D., & Thakurta, A. (2018, July). Differentially private matrix completion revisited. In International Conference on Machine Learning (pp. 2215-2224). PMLR.

[INS19] Iyengar, R., Near, J. P., Song, D., Thakkar, O., Thakurta, A., & Wang, L. (2019, May). Towards practical differentially private convex optimization. In 2019 IEEE Symposium on Security and Privacy (SP) (pp. 299-316). IEEE.

[KST12] Kifer, D., Smith, A., & Thakurta, A. (2012, June). Private convex empirical risk minimization and high-dimensional regression. In Conference on Learning Theory (pp. 25-1). JMLR Workshop and Conference Proceedings.

[KMA19] Kairouz, P., McMahan, H. B., Avent, B., Bellet, A., Bennis, M., Bhagoji, A. N., … & Zhao, S. (2019). Advances and open problems in federated learning. arXiv preprint arXiv:1912.04977.

[KV05] Kalai, Adam, and Santosh Vempala. “Efficient algorithms for online decision problems.” Journal of Computer and System Sciences 71.3 (2005): 291-307.

[KLNRS08] Raskhodnikova, S., Smith, A., Lee, H. K., Nissim, K., & Kasiviswanathan, S. P. (2008). What can we learn privately. In Proceedings of the 54th Annual Symposium on Foundations of Computer Science (pp. 531-540).

[LLV07] Li, N., Li, T., & Venkatasubramanian, S. (2007, April). t-closeness: Privacy beyond k-anonymity and l-diversity. In 2007 IEEE 23rd International Conference on Data Engineering (pp. 106-115). IEEE.

[LT19] Liu, J., & Talwar, K. (2019, June). Private selection from private candidates. In Proceedings of the 51st Annual ACM SIGACT Symposium on Theory of Computing (pp. 298-309).

[M17] Mironov, I. (2017, August). Renyi differential privacy. In Computer Security Foundations Symposium (CSF), 2017 IEEE 30th (pp. 263-275). IEEE.

[MKG07] Machanavajjhala, Ashwin; Kifer, Daniel; Gehrke, Johannes; Venkitasubramaniam, Muthuramakrishnan (March 2007). “L-diversity: Privacy Beyond K-anonymity”. ACM Transactions on Knowledge Discovery from Data.

[NRS07] Nissim, K., Raskhodnikova, S., & Smith, A. (2007, June). Smooth sensitivity and sampling in private data analysis. In Proceedings of the thirty-ninth annual ACM symposium on Theory of computing (pp. 75-84).

[NS08] Narayanan, A., & Shmatikov, V. (2008, May). Robust de-anonymization of large sparse datasets. In Security and Privacy, 2008. SP 2008. IEEE Symposium on (pp. 111-125). IEEE.

[PAE16] Papernot, N., Abadi, M., Erlingsson, U., Goodfellow, I., & Talwar, K. (2016). Semi-supervised knowledge transfer for deep learning from private training data. ICLR 2017.

[PTS21] Papernot, N., Thakurta, A., Song, S., Chien, S., & Erlingsson, U. (2020). Tempered sigmoid activations for deep learning with differential privacy. AAAI 2021.

[RCR15] Rudi, A., Camoriano, R., & Rosasco, L. (2015, December). Less is More: Nyström Computational Regularization. In NIPS (pp. 1657-1665).

[SCS13] Shuang Song, Kamalika Chaudhuri, and Anand D Sarwate. Stochastic gradient descent with differentially private updates. In Proceedings of the 2013 IEEE Global Conference on Signal and Information Processing, GlobalSIP ’13, pages 245–248, Washington, DC, USA, 2013. IEEE Computer Society.

[SPG] Chasing Your Long Tails: Differentially Private Prediction in Health Care Settings. Vinith Suriyakumar, Nicolas Papernot, Anna Goldenberg, Marzyeh Ghassemi. Proceedings of the 2021 ACM Conference on Fairness, Accountability, and Transparency.

[SS98] Samarati, Pierangela; Sweeney, Latanya (1998). “Protecting privacy when disclosing information: k-anonymity and its enforcement through generalization and suppression” (PDF). Harvard Data Privacy Lab. Retrieved April 12, 2017

[SSS17] Shokri, R., Stronati, M., Song, C., & Shmatikov, V. (2017, May). Membership inference attacks against machine learning models. In Security and Privacy (SP), 2017 IEEE Symposium on (pp. 3-18). IEEE.

[SSTT21] Song, S., Thakkar, O., & Thakurta, A. (2020). Evading the Curse of Dimensionality in Unconstrained Private GLMs. In AISTATS 2021.

[XT07] Xiao X, Tao Y (2007) M-invariance: towards privacy preserving re-publication of dynamic datasets. In: SIGMOD conference, Beijing, China, pp 689–700

[YEO21] Yala, A., Esfahanizadeh, H., Oliveira, R. G. D., Duffy, K. R., Ghobadi, M., Jaakkola, T. S., … & Medard, M. (2021). NeuraCrypt: Hiding Private Health Data via Random Neural Networks for Public Training. arXiv preprint arXiv:2106.02484.

[ZHS19] Jingzhao Zhang, Tianxing He, Suvrit Sra, and Ali Jadbabaie. Why gradient clipping accelerates training: A theoretical justification for adaptivity. In International Conference on Learning Representations, 2019.

Posted by Nicolas Papernot and Abhradeep Thakurta on October 25, 2021.