模拟退火原理、详细计算过程及其在BP神经网络中的应用

%% 清空环境变量
warning off    % 关闭报警信息
close all      % 关闭开启的窗口
clear          % 清空变量
clc            % 清空命令行

%% 参数初始化
func = @(x,y)x.^2+y.^2+3*sin(2*x)+3*sin(2*y); % 目标函数
iter = 100;       % 内循环迭代次数
T = 1000;         % 初始温度
dT = 0.9;         % 退火因子
eps = 0.00001;    % 终止温度
history_best = struct('f',[],'ind_x',[],'ind_y',[], 'T',[]);  % 构建结构体，用于存放该温度下的最优解和对应的温度
a = -5; b = 5;
x = a + (b-a) * rand(iter,1);   % 在区间（-5，5）之间随机生成100(内循环迭代次数)个x的值
y = a + (b-a) * rand(iter,1);   % 随机生成100个y的值
%% 内循环 注意：x和y是不断改变的，x和y对应的值算出来的是每次的最优解
while T > eps
    for i = 1:iter
        f = func(x(i), y(i));                        % f 为一次迭代后的值
        [x_new, y_new] = generate_new(x(i),y(i),T);  % 在当前参数点(x(i),y(i)）附近随机选一个新点(x_new, y_new)
        f_new = func(x_new, y_new);                  % 产生新值
        if Metrospolis(f, f_new, T)                  % 判断是否接受新值
            x(i) = x_new; y(i) = y_new;              % 如果接受新值，则把新值的x，y存入x，y数组
        end
    end
    % 根据的迭代iter次记录，获取该温度下的最优解
    [f_best, ind_xy] = best_value(func, x, y, iter);
    history_best.f = [history_best.f, f_best];  % 在行向量末尾追加新数值
    history_best.ind_x = [history_best.ind_x, ind_xy(1)];
    history_best.ind_y = [history_best.ind_y, ind_xy(2)];
    history_best.T = [history_best.T, T];

    T = T * dT; % 按照一定的比例下降温度（退火）
end
 %% 获取全局最优解，和对应的x、y值
[most_best, ind] = best_value(func, history_best.ind_x, history_best.ind_y, iter); 
disp(most_best);
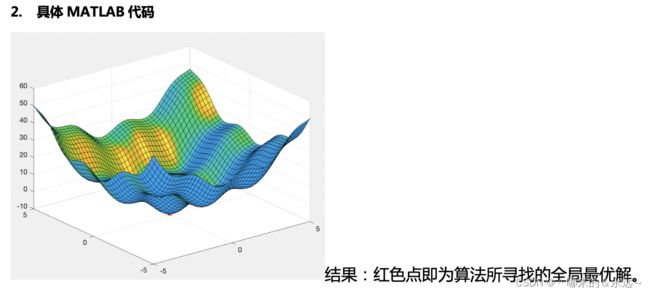
%% 绘图
[xx,yy] = meshgrid(-6:0.2:6,-6:0.2:6);
z = xx.^2+yy.^2+3*sin(2*xx)+3*sin(2*yy);
sl = surfl(xx,yy,z);
% sl.EdgeColor = 'none';
hold on
plot3(ind(1),ind(2),most_best, 'r*',LineWidth=5);

%% 扰动产生新解的过程
function [x_new, y_new] = generate_new(x, y, T)
    while true
        x_new = x + T*(rand() - rand());
        y_new = y + T*(rand() - rand());
        % 重复得到新解，直到产生的新解满足约束条件（-5，5）
        if(-5 < x_new && x_new < 5 && -5 < y_new && y_new < 5 ) 
            break
        end
    end
end

%% Metrospolis准则
function TorF = Metrospolis(f, f_new, T)
    if f_new <= f    % ∆f<0，转移接受，概率为1
        TorF = true;
    else
        x = (f - f_new)/T ;  % ∆f>0，按概率进行转移
        p = exp(x);
        if p > rand()
            TorF = true;
        else
            TorF = false;
        end
    end
end

%% 获取最优目标函数值
function [f_best,idx] = best_value(func, x, y, iter)
    f_list = zeros(1,iter);
    idx = zeros(1,2);

    for i = 1:iter
        f = func(x(i),y(i));  % 计算所有值对应的解
        f_list(i) = f;
    end
    f_best = min(f_list);     % 获取最优解
    [ ~, index] = find(f_list == min(f_list));
    idx(1) = x(index); idx(2) = y(index);  % 最优解下对应的x，y
end

**

四、模拟退火在BP神经网络中的应用

**
借鉴了一篇文章发现模拟退火与BP的结合其实就是：

解释一下Step1和Step2：
1、确定好输入神经元节点个数、隐藏层个数、输出层个数之后，随机赋予搭建好的网络W和b，将W和b送入网络进行训练，得到训练后的权值W和偏置b，并计算该W和b下的误差E1.
2、利用模拟退火算法，将连接权值作为随机扰动，即每一个连接权值加上一个“随机数”，W_new = W +∆W，b_new = b +∆b其实就是产生扰动新解的过程。
3、将W_new 和 b_new作为初始权值和阈值，送入网络进行训练，并计算误差E2.

其实我加了模拟退火对数据进行分类，准确率并没有提升，训练还花很多时间。但有些人可能还是想要了解模拟退火与BP是怎么结合的，所以我这边就根据我的理解编写了代码，不对的部分请多指教。
把数据改成自己的就行。

%% 清空环境变量
warning off    % 关闭报警信息
close all      % 关闭开启的窗口
clear          % 清空变量
clc            % 清空命令行

%% 导入数据
res = load("rock_train_data.mat");

%% 划分训练集和测试集

P_train = res.data(1:1700,1:28)';
T_train = res.data(1:1700,29)';
M = size(P_train, 2); % 数据长度

P_test = res.data(1701:end,1:28)';
T_test = res.data(1701:end,29)';
N = size(P_test, 2); % 数据长度

%% 数据归一化
[p_train, ps_input] = mapminmax(P_train,0,1);
p_test = mapminmax('apply', P_test, ps_input);
t_train = ind2vec(T_train);
t_test = ind2vec(T_test);

inputnum = size(p_train, 1);          % 输入层神经元个数
outputnum = size(t_train, 1);         % 输出层神经元个数
hiddennum = 40;                 % 隐藏层神经元个数

nvar_best = SA_callbackfun(p_train,t_train,p_test, t_test, hiddennum);

disp("退火结束！开始利用获得的最优初始化权重与阈值训练BP神经网络");
%% 新建BP网络
net = newff(p_train, t_train, hiddennum);

%% 设置网络参数：训练次数为1000次，训练目标为0.01，学习速率为0.1
net.trainParam.epochs = 1000;
net.trainParam.goal = 0.01;
net.trainParam.lr = 0.1;
%% 神经网络初始权值和阈值
w1num = inputnum * hiddennum;           % 输入层到隐含层的权值个数
w2num = outputnum * hiddennum;          % 隐含层到输出层的权值个数
w1 = nvar_best(1 : w1num);                      % 初始输入层到隐含层的权值
B1 = nvar_best(w1num + 1 : w1num + hiddennum);  % 隐含层神经元阈值
w2 = nvar_best(w1num + hiddennum + 1 : w1num + hiddennum + w2num);  % 初始隐含层到输出层的权值
B2 = nvar_best(w1num + hiddennum + w2num + 1 : w1num + hiddennum + w2num + outputnum);  % 输出层阈值
net.iw{1, 1} = reshape(w1, hiddennum, inputnum);            % 输入层到隐含层的权值
net.lw{2, 1} = reshape(w2, outputnum, hiddennum);           % 隐含层到输出层的权值
net.b{1} = reshape(B1, hiddennum, 1);
net.b{2} = reshape(B2, outputnum, 1);
%% 训练网络
net = train(net, p_train, t_train);
%% 测试网络
%% sim仿真测试
t_sim1 = sim(net, p_train);
t_sim2 = sim(net, p_test);

%% 数据反归一化
T_sim1 = vec2ind(t_sim1);
T_sim2 = vec2ind(t_sim2);

%% 数据排序
[T_train, index_1] = sort(T_train);
[T_test, index_2] = sort(T_test);

T_sim1 = T_sim1(index_1);
T_sim2 = T_sim2(index_2);

%% 性能评估
error_train = sum((T_sim1 == T_train))/M*100;
error_test = sum((T_sim2 == T_test))/N*100;

%% 绘图
figure
plot(1:M, T_train, 'r-*',1:M,T_sim1,'b-o','LineWidth',1)
legend('真实值','预测值')
xlabel('预测样本')
ylabel('预测结果')
string = {'训练集预测结果对比';['准确率=' num2str(error_train) '%']};
title(string);
xlim([1,M]);

figure
plot(1:N, T_test, 'r-*',1:N,T_sim2,'b-o','LineWidth',1)
legend('真实值','预测值')
xlabel('预测样本')
ylabel('预测结果')
string = {'训练集预测结果对比';['准确率=' num2str(error_test) '%']};
title(string);
xlim([1,N]);

%% 混淆矩阵
figure
cm = confusionchart(T_train, T_sim1);
cm.Title = 'Confusion Matrix for Train Data';
cm.ColumnSummary = 'column-normalized';
cm.RowSummary = 'row-normalized';

figure
cm = confusionchart(T_test, T_sim2);
cm.Title = 'Confusion Matrix for Test Data';
cm.ColumnSummary = 'column-normalized';
cm.RowSummary = 'row-normalized';

function nvar_best = SA_callbackfun(p_train,t_train,p_test, t_test, hiddenSize)
    % P_train： 训练数据
    % T_train： 训练数据对应的标签
    % P_test： 测试数据
    % T_test： 测试数据对应的标签
    % hiddenSize：隐藏层对应的神经元个数
    
    %% BP网络神经元设置
    input_num = size(p_train,1);        % 输入层神经元个数
    output_num = size(t_train,1);       % 输出层神经元个数
    
    hiddenLayerSize = hiddenSize;       % 隐藏层神经元个数
    
    w1Num = input_num*hiddenLayerSize;  % 输入层到隐藏层的权重w个数
    w2Num = hiddenLayerSize*output_num; % 隐藏层到输出层的权重w个数
    b1 = hiddenLayerSize;               % 输入层到隐藏层的偏置b个数
    b2 = output_num;                    % 隐藏层到输出层的偏置b个数
    
    nvar = w1Num+w2Num+b1+b2;           % 总共需要调节的参数个数
    
    %% SA算法主程序
    lb = -1*ones(nvar,1);                 % 参数取值下界
    ub = ones(nvar,1);                    % 参数取值上界
    % 冷却表参数
    MarkovLength = 10;                    % 马可夫链长度(内循环次数)
    DecayScale = 0.85;                    % 衰减参数
    StepFactor = 0.2;                     % Metropolis步长因子，控制扰动新解
    Temperature0 = 8;                     % 初始温度
    Temperatureend = 3;                   % 最终温度
    Boltzmann_con = 1;                    % Boltzmann常数
    AcceptPoints = 0.0;                   % Metropolis过程中总接受点
    
    %% 随机初始化参数
    lb = -1;                   % 参数取值下界
    ub = 1;                    % 参数取值上界
    
    Par_cur = lb + (ub-lb) * rand(nvar,1);   % 用Par_cur表示当前解
    Par_best = lb + (ub-lb) * rand(nvar,1);  % 用Par_best表示冷却中的最好解
        
    
    disp("开始进行模拟退火，进行参数寻优：");
    % 计算误差
    Par_best_err = objfunBP(Par_best,p_train, t_train, hiddenLayerSize,p_test,t_test);
    Par_cur_err = objfunBP(Par_best,p_train, t_train, hiddenLayerSize,p_test,t_test);
            
    %% 每迭代一次退火(降温)一次，直到满足迭代条件为止
    T = Temperature0;
    itr_num = 0;                          % 记录迭代数
    while T>Temperatureend
        
        for i = 1:MarkovLength
            % 在此当前参数点附近随机选下一点
            p=0;
            while p==0
                Par_new = Par_cur+StepFactor.*(rand() - rand());  % 扰动产生新解的过程
                % 防止越界
                if max(Par_new)<ub && min(Par_new)>lb
                    p=1;
                end
            end
            disp("训练Par_new_err")
            % 计算扰动新解的误差
            Par_new_err = objfunBP(Par_best,p_train, t_train, hiddenLayerSize,p_test,t_test);
           
            % 检验当前解是否为全局最优解，即判断经过SA优化的初始化参数训练出来的网络误差大小
            % Metropolis过程
            if (Par_cur_err > Par_new_err)           
                % 接受新解
                Par_cur = Par_new;
                Par_cur_err = Par_new_err;
                AcceptPoints = AcceptPoints+1;
            else
                changer = -1*(Par_new_err - Par_cur_err)/(Boltzmann_con * T);
                p1 = exp(changer);
                if p1 > rand
                    Par_cur = Par_new;
                    Par_cur_err = Par_new_err;
                    AcceptPoints = AcceptPoints+1;
                end
            end
           % 更新MarkovLength过程中的最优解
            if (Par_best_err > Par_new_err)
                Par_best = Par_new;        % 将新解保存为最优解
                Par_best_err = Par_new_err;
            end
        end   
        % 退火
        itr_num = itr_num + 1;
        T = DecayScale*T;                   % 温度更新（降温)
        disp(['第',num2str(itr_num),'次退火结束!']);
        disp(itr_num);
    end
    
    %% 获得最优的nvar
    nvar_best = Par_best';
end

function err= objfunBP(nvar, p_train, t_train, hiddennum, p_test, t_test)
    
    %% 训练与测试BP网络
    %% 输入
    % nvar:网络的初始权值和阈值
    % P:训练样本输入
    % T:训练样本输出
    % hiddennum:隐含层神经元数
    % P_test:测试样本输入
    % T_test:测试样本期望输出
    %% 输出
    % err:预测样本的预测误差的范数
    inputnum = size(p_train, 1);          % 输入层神经元个数
    outputnum = size(t_train, 1);         % 输出层神经元个数
   
    %% 建立BP前馈神经网络
    net = newff(p_train, t_train, hiddennum);

    %% 设置网络参数：训练次数为1000次，训练目标为0.01，学习速率为0.1
    net.trainParam.epochs = 1000;
    net.trainParam.goal = 0.0001;
    net.trainParam.lr = 0.1;
    
    %% 神经网络初始权值和阈值
    w1num = inputnum * hiddennum;           % 输入层到隐含层的权值个数
    w2num = outputnum * hiddennum;          % 隐含层到输出层的权值个数
    w1 = nvar(1 : w1num);                      % 初始输入层到隐含层的权值
    B1 = nvar(w1num + 1 : w1num + hiddennum);  % 隐含层神经元阈值
    w2 = nvar(w1num + hiddennum + 1 : w1num + hiddennum + w2num);  % 初始隐含层到输出层的权值
    B2 = nvar(w1num + hiddennum + w2num + 1 : w1num + hiddennum + w2num + outputnum);  % 输出层阈值
    net.iw{1, 1} = reshape(w1, hiddennum, inputnum);            % 输入层到隐含层的权值
    net.lw{2, 1} = reshape(w2, outputnum, hiddennum);           % 隐含层到输出层的权值
    net.b{1} = reshape(B1, hiddennum, 1);
    net.b{2} = reshape(B2, outputnum, 1);
    %% 训练网络
    net = train(net, p_train, t_train);
    %% 测试网络
    Y = sim(net, p_test);
    err = norm(Y - t_test);
    net.trainParam.show = NaN;
    net.trainParam.showwindow = false;      % 使用高版本MATLAB不显示图形框
end