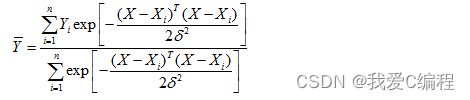m基于GA遗传优化的GRNN广义回归神经网络销售数据预测算法matlab仿真

目录

1.算法描述

2.仿真效果预览

3.MATLAB核心程序

4.完整MATLAB

---

1.算法描述

      随着市场经济的发展和全球化，国内外企业面临着越来越残酷的市场竞争，要想赢得竞争，赢得市场，从事商品销售的单位必须在短时间内，以最低的成本将产品提供给客户，这使得对市场的变化和本身业务的发展前景进行估计。

        制冷压缩机的主要功能是将低压气体提升为高压气体，是制冷设备的核心部件，其广泛应用在空调冰箱等各类电器设备中。因此制冷压缩机有着十分广泛的市场前景，为了获得较为准确的市场预期，我们需要使用已有的理论知识和科学方法，对制冷压缩机的市场发展趋势进行预先估计，从而进一步减少风险，避免企业决策的盲目性。

      遗传算法（Genetic Algorithm）是一类借鉴生物界的进化规律演化而来的随机化搜索方法。它是由美国的J.Holland教授1975年首先提出，其主要特点是直接对结构对象进行操作，不存在求导和函数连续性的限定；具有内在的隐并行性和更好的全局寻优能力；采用概率化的寻优方法，能自动获取和指导优化的搜索空间，自适应地调整搜索方向，不需要确定的规则。遗传算法的这些性质，已被人们广泛地应用于组合优化、机器学习、信号处理、自适应控制和人工生命等领域。它是现代有关智能计算中的关键技术。

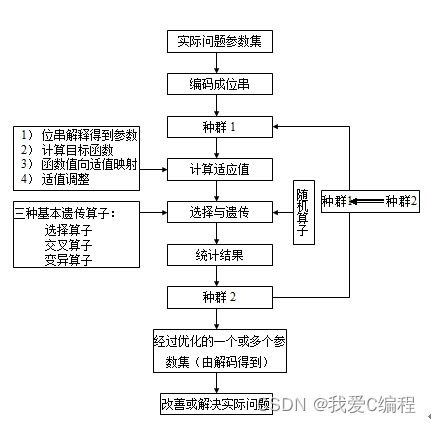
       算法的算法流程图如下图所示：

从图1的算法流程图可知，遗传算法，其主要步骤如下所示：

        步骤一、选择问题解的一个编码，给出一个包含N个染色体的初始种群。

        步骤二、对种群中的每一个染色体 ，分别计算其对应的适应函数值。

        步骤三、若停止规则满足，则算法停止，否则计算概率P，并以此概率分布，从中随机选取N个染色体构成一个新的种群。

        步骤四、通过交叉(交叉概率为)，得到N个染色体的交叉概率值。

        步骤五、以较小的变异概率，使得某染色体的一个基因发生变异，形成新的群体重复第步骤二步。

       对GRNN网络来说，当确定了学习样本，则相应的网络结构和各神经元之间的连接权值也就确定出来，网络的训练实际上只是确定平滑参数的过程。GRNN网络中的即相当于径向基函数的分布密度SPREAD。一般情况下，SPREAD越大，逼近过程就越平滑，但误差也增大；SPREAD越小，函数逼近越精确，但逼近过程也越不平滑。

      平滑参数的取值会在很大程度上影响着广义回归神经网络的预测性能，根据式子：

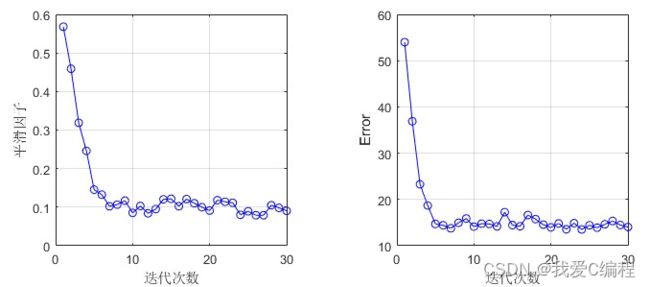
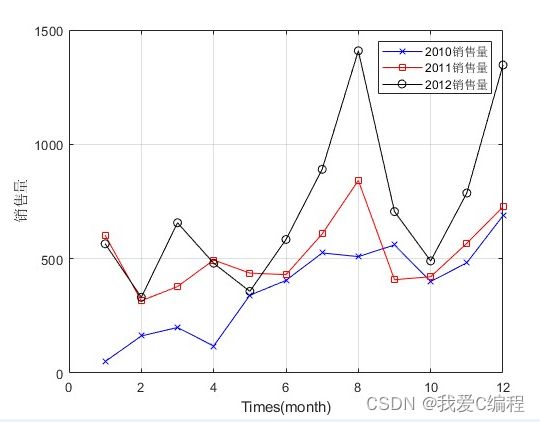
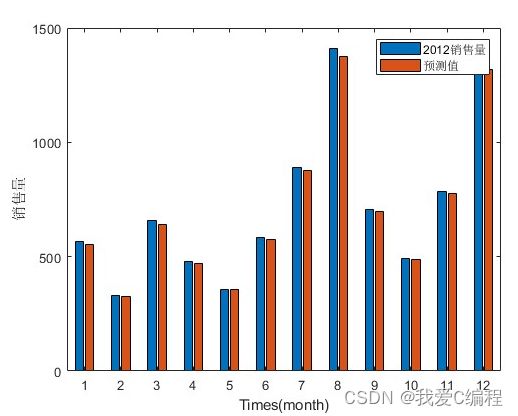
2.仿真效果预览

matlab2022a仿真结果如下：

 

 

 

 

3.MATLAB核心程序

data     = [data2010',data2011',data2012'];
data0    = data;
%归一化
Xmin     = min(data);
Xmax     = max(data);
data     = (data-min(data))/(max(data)-min(data));
 
figure;
plot(data(1:12),'b-x');
hold on
plot(data(13:24),'r-s');
hold on
plot(data(25:36),'k-o');
hold on
legend('2010销售量','2011销售量','2012销售量');
xlabel('Times(month)');
ylabel('销售量');
axis([0,12,0,1]);
grid on;
figure;
plot(data0(1:12),'b-x');
hold on
plot(data0(13:24),'r-s');
hold on
plot(data0(25:36),'k-o');
hold on
legend('2010销售量','2011销售量','2012销售量');
xlabel('Times(month)');
ylabel('销售量');
axis([0,12,0,1500]);
grid on;
%%
%使用遗传算法获得最优的平滑参数
MAXGEN = 30;
NIND   = 50;
Chrom  = crtbp(NIND,1*10);
 
%14个变量的区间
%优化变量如下：
%多边形个数N，1~100
Areas  = [0;
          1];
 
FieldD = [rep([10],[1,1]);Areas;rep([0;0;0;0],[1,1])];
 
alpha  = zeros(NIND,1);
alphas = zeros(MAXGEN,1);
 
 
for a=1:1:NIND 
    a
    alpha(a)= 0.5;       
    %计算对应的目标值
    Result = func_obj(alpha(a),data,Xmax,Xmin);
    E      = mean(abs(Result-data0(25:36)));
    J(a,1) = E;
end
Objv  = J;
gen   = 0; 
 
while gen < MAXGEN;   
      gen
      FitnV=ranking(Objv);    
      Selch=select('sus',Chrom,FitnV);    
      Selch=recombin('xovsp', Selch,0.95);   
      Selch=mut( Selch,0.05);   
      phen1=bs2rv(Selch,FieldD);   
      
      for a=1:NIND  
          alpha(a)= phen1(a,1);      
          %计算对应的目标值
          Result  = func_obj(alpha(a),data,Xmax,Xmin);
          E       = mean(abs(Result-data0(25:36)));
          JJ(a,1) = E;
      end 
      Objvsel      = JJ;    
      [Chrom,Objv] = reins(Chrom,Selch,1,1,Objv,Objvsel);   
      gen          = gen + 1; 
      Error(gen)   = mean(JJ);
      alphas(gen)  = mean(alpha);
end 
Result  = func_obj(alphas(end),data,Xmax,Xmin);
%画图
figure;
subplot(121)
plot(alphas,'b-o');
hold on;
xlabel('迭代次数');
ylabel('平滑因子');
axis square;
grid on;
 
subplot(122)
plot(Error,'b-o');
hold on;
xlabel('迭代次数');
ylabel('Error');
axis square;
grid on;
 
load NET.mat
Result  = sim(net,1:12);
Result  = Result*(Xmax-Xmin)+Xmin;
 
figure
plot(data0(25:36),'b-o');
hold on
plot(Result,'r-s');
legend('2012销售量','预测值');
xlabel('Times(month)');
ylabel('销售量');
grid on;
 
figure
S = [data0(25:36);Result]';
bar(S);
legend('2012销售量','预测值');
xlabel('Times(month)');
ylabel('销售量');
save Rgrnn.mat Result
A = (Result-data0(25:36))./Result;
A = 100*A';
A
02_021m

4.完整MATLAB

matlab源码说明_我爱C编程的博客-CSDN博客

V