SVD 理解及使用

SVD 理解及使用

奇异值分解（SVD）原理与在降维中的应用

奇异值分解（SVD）是机器学习领域中广泛应用的算法，它不光可以用于降维算法中的特征分解，还可以用于推荐系统，以及自然语言处理等领域。是很多机器学习算法的基石。本文就对SVD的原理做一个总结，并讨论SVD是如何被应用于降维的。

关于特征值和特征向量

首先我们先回顾一下特征值和特征向量的定义：
$$Ax=\lambda x⟹(\lambda E-A)x=0$$
其中A是一个n × n的实对称矩阵，x 是一个n维的向量，则我们说$\lambda$是矩阵A的一个特征值，而x是矩阵A的特征值$\lambda$s所对应的特征向量。
求出特征值和特征向量后我们可以讲矩阵A特征进行分解。例如我们求出了矩阵A的n个特征值 ${\lambda }_1\le {\lambda }_2\le ...\le {\lambda }_n$ 以及对应的n个特征值所对应的向量 $\{w_1,w_2,...w_n\}$,如果这n个特征向量线性无关(可以看作是沿x轴的向量和沿着y轴的向量这种类似的，也就是说特征向量之间两两垂直)，那么矩阵A就可以用下式的特征分解表示：
$$A=W\sum W^{-1}$$
其中W是这n个特征向量所拼接成的n×n维矩阵，而$\sum$为这n个特征值为主对角线的n×n维矩阵。

而一般我们会将W对应的n个特征向量进行标准化，即满足$||w_i|{|}_2=1$(转化为单位向量) ,或者说$w_i^T{w}_i=1$,此时W的n个特征向量为标准正交基，即满足$W^{T}W=I$，即$W^T=W^{-1}$。因此我们的特征分解表达式可写为:
$$A=W\sum W^T$$

注意： 在进行特诊分解的时候，矩阵A必须为方阵，若出现行列的长度不同时则需要使用后面的SVD了。

SVD 的定义

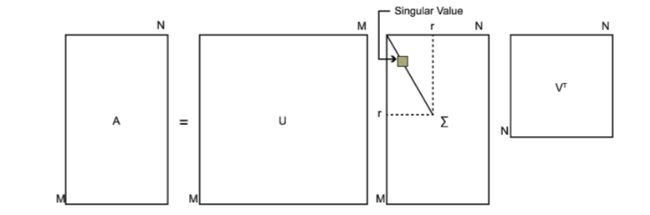
SVD也是对矩阵进行分解，但是和特征分解不同，SVD并不要求分解的矩阵为方块。在SVD中对于一个m×n的矩阵，我们可以定义矩阵的SVD为：
$$A=U\sum V^T$$
其中U是一个m×m的矩阵，$\sum$是一个m×n的矩阵，处理主对角线上的元素外全为0，主对角线上的每个元素都为奇异值，V是一个n×n的矩阵。U和V满足$U^{T}U=I,V^{T}V=I$。

后面我们就来推导这个公式是如何来的

我们可以利用上面特征值分解中得到的结论进行迁移，而上一小节特征值分解中的公式适用于方阵，那么我们如何进行转化呢？

为了使用上一小结我们可以利用这样一个技巧也就是我们先对$A^{T}A$进行特征分解，此时$A^{T}A$为n×n的方阵，可以得到以下公式:
$$\begin{gathered} A=U\sum V^T\Rightarrow A^T=V{\Sigma }^T{U}^T\Rightarrow A^{T}A=V\sum U^{T}U\sum V^T \\ =V{\Sigma }^T{U}^{T}U\Sigma V^T \\ =V{\Sigma }^2{V}^T \end{gathered}$$
在上式的证明中我们使用了:$U^{T}U=I,{\Sigma }^T\Sigma ={\Sigma }^2$。此时我们对应第二节中的结论，可以看出对$A{A}^T$的特征向量组成的就是我们的SVD中的U矩阵。所有不同的只是中间的特特征值和奇异值，也就是说特征值和奇异值满足以下关系：
$${\sigma }_i=\sqrt{{\lambda }_i}$$
简单的描述就是说A的奇异值等于$A^{T}A$对应特征值的开平方。

SVD 的一些性质

关于这部分找了许多相关资料，许多都是按照下面来进行解释的。

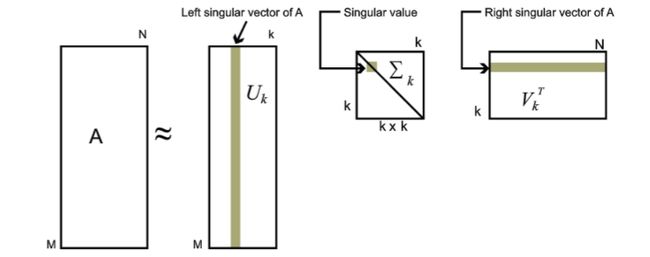
对于奇异值,它跟我们特征分解中的特征值类似，在奇异值矩阵中也是按照从大到小排列，而且奇异值的减少特别的快，在很多情况下，前10%甚至1%的奇异值的和就占了全部的奇异值之和的99%以上的比例。也就是说，我们也可以用最大的k个的奇异值和对应的左右奇异向量来近似描述矩阵。也就是说：
$$A_{m\times n}=U_{m\times n}{\Sigma }_{m\times n}{V}_{n\times n}^T\approx U_{m\times k}{\Sigma }_{k\times k}{V}_{k\times n}^T$$
其中k要比n小很多，也就是一个大的矩阵A可以用三个小的矩阵Um×k,Σk×k,VTk×nUm×k,Σk×k,Vk×nT来表示。如下图所示，现在我们的矩阵A只需要灰色的部分的三个小矩阵就可以近似描述了。(这样我们就减少了我们要存储表达A矩阵数据的大小)

由于这个重要的性质，SVD可以用于PCA降维，来做数据压缩和去噪。

个人的理解

对于奇异向量我们可以理解为要表达A这个矩阵所需要的维度，例如我们有三个向量(1,2)、(3,1)、(1,1) , 那么我们至少需要两个基向量就可以表示所有的这些向量，例如（1,0）和（0,1） 。

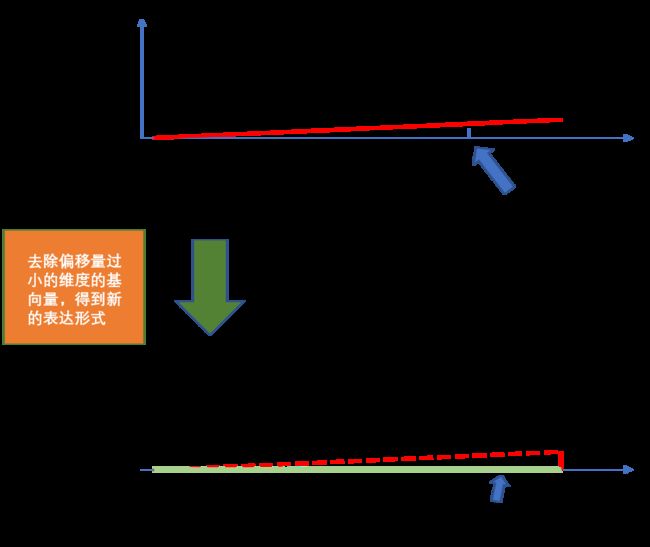
那么如何理解降维降噪的作用呢，我们可以结合下图

可以从上图中看到，原始数据在y轴方向（维度）上的偏移量很小。那么我们就忽略y方向对应的基向量(y对应的这个维度)，对数据进行重新表达（投影）得到L‘ ,而L’又可以很好的代表原始的数据L。这样我们就对原始数据进行了降维处理。
如何理解降噪呢？其实有时候数据中类类似于像y方向上的微小偏移是一些不确定的因素造成的并不是数据真正想表达的（或者说这个维度的信息并不重要)。

理解了上面这个之后我们就可以清楚为什么要删除SVD表达式$A=U\sum V^T$中较小奇异值对应的奇异向量，这里奇异值可以类比于上图的偏移量而奇异向量可理解为上图中y方向对应的向量。

SVD 代码实现

我们利用SVD对图像进行压缩处理。

原图

代码

import math
from itertools import count
from PIL import Image
import numpy as np
import matplotlib.pyplot as plt

def img_compress(img,percent):
  """
      图像压缩

      :param img: 矩阵数据
      :param percent: 奇异向量保留百分比
  """
  U,s,VT = np.linalg.svd(img)   ## 直接获得奇异矩阵分解的三个部分
  Sigma = np.zeros(np.shape(img))
  Sigma[:len(s),:len(s)] = np.diag(s)
  # 根据压缩比 取k值

  count = (int)(sum(s))*percent
  k = -1
  curSum = 0
  while curSum <= count:
      k+=1
      curSum += s[k]
  # 还原后的数据D
  D = U[:,:k].dot(Sigma[:k,:k].dot(VT[:k,:]))
  D[D<0] = 0
  D[D>255] = 255
  return np.rint(D).astype('uint8')

# 图像重建
def rebuild_img(filename,percent,pen):
  img = Image.open(filename,'r')
  a = np.array(img)
  R0 = a[:,:,0]
  G0 = a[:,:,1]
  B0 = a[:,:,2]
  R = img_compress(R0,percent)
  G = img_compress(G0,percent)
  B = img_compress(B0,percent)
  re_img = np.stack((R,G,B),2)
  pen.imshow(re_img)

def test():
  fig=plt.figure(figsize=(20, 12))
  columns = 3
  rows = 3
  for i in range(columns * rows):
    ax = fig.add_subplot(rows, columns, i + 1)
    ax.axis('off')
    ax.set_title(f"{round(1-0.08*i,2)*100}%")
    rebuild_img('pic_1.jpg',1-0.08*i,ax)

if __name__ == '__main__':
  test()
  plt.show()

压缩结果

可以根据测试结果看到使用SVD删除少部分奇异向量后重构得到的数据(上面为图片的方式传达)几乎几乎保留了原始数据的特征。