路径规划-Minimum snap轨迹优化
传统的路径规划pipeline包括路径搜索和轨迹优化两部分。

轨迹优化的目的是生成光滑轨迹,其必要性如下:
- 适合移动机器人的自主移动
- 速度和加速度等动力学状态无法突变
- 移动机器人不必在拐角处加速和减速
- 节约能量
1.预备知识
1.1 轨迹优化的一般过程
- 存在边界条件:起始点和终止点
- 中间节点:包括 A ∗ A^* A∗、 R R T ∗ RRT^* RRT∗寻找到的中继节点
- 平滑规则:给出一个评价函数评价轨迹的光滑程度
1.2 微分平坦(Differential Flatness)
微分平坦对于非线性系统来说,可以类比为线性系统里的能控性。
以无人机的使用为例,其状态空间可以使用4个变量表示: σ = [ x , y , z , Φ ] \sigma=[x,y,z,\Phi] σ=[x,y,z,Φ],其中 Φ \Phi Φ为偏航角。
微分平坦的证明:
无人机的状态空间共有12个变量 σ = [ x , y , z , ϕ , θ , Φ , x ˙ , y ˙ , z ˙ , w x , w y , w z ] \sigma=[x,y,z,\phi,\theta,\Phi,\dot{x},\dot{y},\dot{z},w_x,w_y,w_z] σ=[x,y,z,ϕ,θ,Φ,x˙,y˙,z˙,wx,wy,wz]
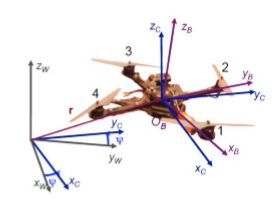
其非线性都动力学可以使用下面的平移方程和转动方程表示:
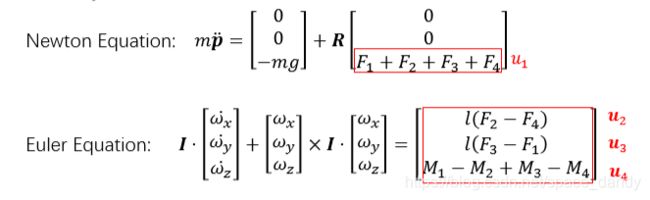
上述方程等价于下述表示形式
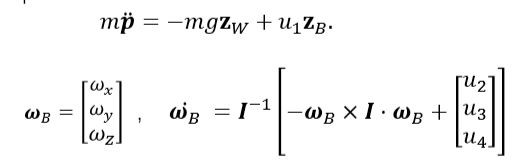
主要证明 [ x , y , z , ϕ , θ , Φ , x ˙ , y ˙ , z ˙ , w x , w y , w z ] [x,y,z,\phi,\theta,\Phi,\dot{x},\dot{y},\dot{z},w_x,w_y,w_z] [x,y,z,ϕ,θ,Φ,x˙,y˙,z˙,wx,wy,wz] 12个状态变量可以被 [ x , y , z , Φ ] [x,y,z,\Phi] [x,y,z,Φ] 4个状态变量通过代数组合表示出来。其中, x ˙ , y ˙ , z ˙ \dot{x},\dot{y},\dot{z} x˙,y˙,z˙三个变量为 x , y , z x,y,z x,y,z的导数,可以直接被其表示。

如上图所示,无人机机体坐标系为 [ x B , y B , z B ] [x_B,y_B,z_B] [xB,yB,zB],得到无人机机体坐标系后可以通过欧拉角等计算得到俯仰角、滚转角和偏航角(即 ϕ , θ , Φ \phi,\theta,\Phi ϕ,θ,Φ)。其中,无人机的合加速度方向为(垂直于无人机机体),即 z B z_B zB可以使用 x , y , z x,y,z x,y,z的二阶导和重力加速度表示:

求取 x B x_B xB和 y B y_B yB,引入中间坐标系 [ x C , y C , z W ] [x_C,y_C,z_W] [xC,yC,zW](见上图),其中:
![]()
θ 4 \theta_4 θ4为偏航角 Φ \Phi Φ,则 x B x_B xB和 y B y_B yB可以通过以下叉乘计算得到
![]()
下面观察 w x , w y , w z w_x,w_y,w_z wx,wy,wz的表示。首先对移动方程求导得到:

w B W w_{BW} wBW表示世界坐标系下看到的机体角速度。同时,对于 u 1 u_1 u1有:
![]()
代回前式,有:
![]()
w B W w_{BW} wBW的计算方式为:
![]()
代入 h w h_w hw的计算公式得到:
h w = − w x ∗ y B + w y ∗ x B h_w=-w_x*y_B+w_y*x_B hw=−wx∗yB+wy∗xB
上式同时两边点乘 y B y_B yB得到 h w ∗ y B = − w x h_w*y_B=-w_x hw∗yB=−wx,同理两边点乘x_B得到 h w ∗ x B = w y h_w*x_B=w_y hw∗xB=wy。整理得:
![]()
由于 w B W = w B C + w C W w_{BW}=w_{BC}+w_{CW} wBW=wBC+wCW,且 w B C w_{BC} wBC不含有 z B z_B zB分量:
![]()
无人机的控制回路
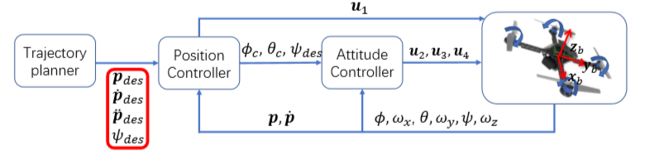
通过轨迹规划得到的位置信息( p d e s p_{des} pdes),速度信息(位置信息的导数),加速度信息(位置信息的二阶导)和偏航角输入位置控制器,计算出推力 u 1 u_1 u1和姿态信息,将姿态信息输入姿态控制器解算出三个方向的力矩 u 2 , u 3 , u 4 u_2,u_3,u_4 u2,u3,u4, u 1 , u 2 , u 3 , u 4 u_1,u_2,u_3,u_4 u1,u2,u3,u4共同完成对无人机的控制。
2.轨迹生成
令生成的轨迹为多项式,原因如下:
- 多项式满足光滑准则
- 容易计算导数
- 方便在3个维度上生成轨迹
2.1 Minimum-snap的建立
- List item
对于一带有多个节点的轨迹图,可以使用分段多项式进行描述:

Minimum Snap的最小化目标函数为snap(jerk的导数,jerk为加速度的导数),对于一段轨迹,最小化jerk选择的阶数为5(2x3-1,3个未知量分别为位置、速度、加速度),最小化snap选择的阶数为7(2x4-1,4个未知量分别为位置、速度、加速度、jerk)。实际过程中,考虑最坏情况,k段距离阶数的选择与1段轨迹相同。
- 等式约束,即一些边界条件:
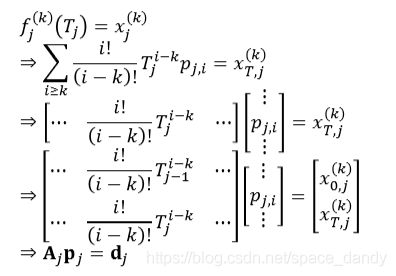
一个简单的例子表示如下:

- 连续性约束(节点两边的n阶导相同):

整理得到最终构造的约束问题为:

该问题为一个典型的二次优化问题(quadratic programming,QP)。
2.2 Minimum-snap的求解
决策变量映射
优化问题优化的多项式的系数 p 1 p_1 p1到 p M p_M pM。
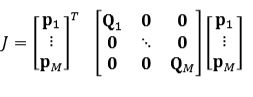
该问题将对轨迹系数的优化问题转化为对各个边界(轨迹上的各个节点)的导数约束的优化问题。通过构建映射矩阵 M j M_j Mj对多项式系数进行映射,得到 M j p j = d j M_jp_j=d_j Mjpj=dj,即:

给出一个构建M矩阵的例子如下:

可以看出M可以通过将某段轨迹初始时刻t=0和末尾时刻t=T代入上市得到。
利用选择矩阵求解
该问题求解的关键在于通过选择矩阵C将映射后的决策变量分解为已经固定的变量 d F d_F dF和未固定的变量 d P d_P dP,代回J如下:

对 d P d_P dP求偏导,使求导后等于0:


