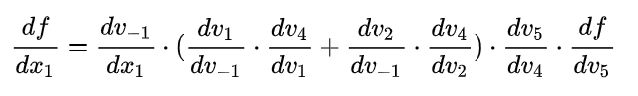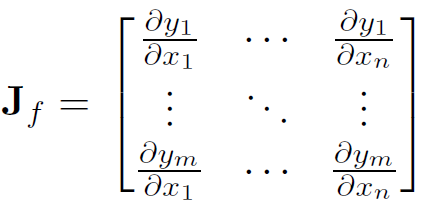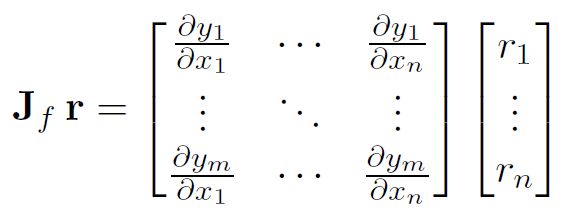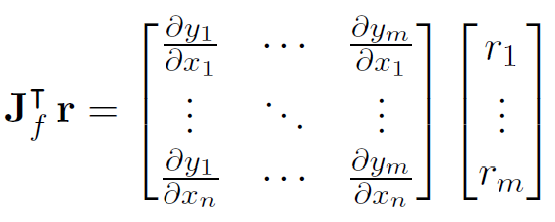深度学习利器之自动微分(2)
深度学习利器之自动微分(2)
文章目录
- 深度学习利器之自动微分(2)
-
- 0x00 摘要
- 0x01 前情回顾
- 0x02 自动微分
-
- 2.1 分解计算
- 2.2 计算模式
- 2.3 样例
- 2.4 前向模式(Forward Mode)
-
- 2.4.1 计算过程
- 3.4.2 推广
- 3.4.3 问题
- 3.5 反向模式(Reverse Mode)
-
- 3.5.1 思路
- 3.5.2 计算过程
- 3.5.3 推广
- 3.5.4 内存问题和inplace 操作
- 3.6 比较
- 0x04 PyTorch
-
- 4.1 原理
-
- 4.1.1 雅克比矩阵
-
- backward 函数
- torch.autograd 类
- 4.1.2 计算图
- 4.1.3 神经网络中的链式法则
- 4.2 PyTorch 功能
-
- 4.2.1 方法1 backward
- 4.2.2 方法2 grad
- 4.3 模拟印证
-
- 4.3.1 原始版本
- 4.3.2 前向模式
- 4.3.3 反向模式
- 0xEE 个人信息
- 0xFF 参考
0x00 摘要
本文和上文以 Automatic Differentiation in Machine Learning: a Survey为基础,逐步分析自动微分这个机器学习的基础利器。
深度学习框架,帮助我们解决的核心问题就是两个:
- 反向传播时的自动梯度计算和更新,也就是自动微分。
- 使用 GPU 进行计算。
本文就具体介绍自动微分究竟是什么。
0x01 前情回顾
上文深度学习利器之自动微分(1)中,我们介绍了一些基础概念,常见微分方法和自动微分的数学基础。
在数学与计算代数学中,自动微分或者自动求导(Automatic Differentiation,简称AD)也被称为微分算法或数值微分。它是一种数值计算的方式,其功能是计算复杂函数(多层复合函数)在某一点处对某个的导数,梯度,Hessian矩阵值等等。
自动微分又是一种计算机程序,是深度学习框架的标配,是反向传播算法的泛化。开发者写的任何模型都需要靠自动微分机制来计算梯度,从而更新模型。它的原理实际上是通过记录运算顺序,利用已经定义好的导数规则,生成一个与正常计算程序对偶的程序。
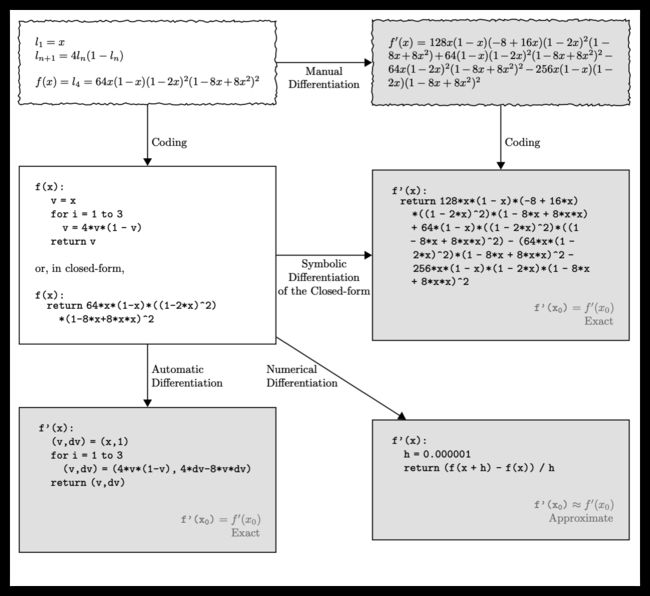
微分的几种比较常用的方法如下:
- 手动求解法(Manual Differentiation) : 完全手动完成,依据链式法则解出梯度公式,带入数值,得到梯度。
- 数值微分法(Numerical Differentiation) :利用导数的原始定义,直接求解微分值。
- 符号微分法(Symbolic Differentiation) : 利用求导规则对表达式进行自动计算,其计算结果是导函数的表达式而非具体的数值。即,先求解析解,然后转换为程序,再通过程序计算出函数的梯度。
- 自动微分法(Automatic Differentiation) :介于数值微分和符号微分之间的方法,采用类似有向图的计算来求解微分值。
具体如下图:
接下来我们就具体研究一下自动微分。
0x02 自动微分
2.1 分解计算
自动微分的精髓在于它发现了微分计算的本质:微分计算就是一系列有限的可微算子的组合。
自动微分法被认为是对计算机程序进行非标准的解释。自动微分基于一个事实,即每一个计算机程序,不论它有多么复杂,都是在执行加减乘除这一系列基本算数运算,以及指数、对数、三角函数这类初等函数运算。于是自动微分先将符号微分法应用于最基本的算子,比如常数,幂函数,指数函数,对数函数,三角函数等,然后代入数值,保留中间结果,最后再通过链式求导法则应用于整个函数。
通过将链式求导法则应用到这些运算上,我们能以任意精度自动地计算导数,而且最多只比原始程序多一个常数级的运算。
我们以如下为例,这是原始公式
y = f ( g ( h ( x ) ) ) = f ( g ( h ( w 0 ) ) ) = f ( g ( w 1 ) ) = f ( w 2 ) = w 3 y=f(g(h(x)))=f(g(h(w_0)))=f(g(w_1))=f(w_2)=w_3 \\ y=f(g(h(x)))=f(g(h(w0)))=f(g(w1))=f(w2)=w3
自动微分以链式法则为基础,把公式中一些部分整理出来成为一些新变量,然后用这些新变量整体替换这个公式,于是得到:
KaTeX parse error: No such environment: align at position 8: \begin{̲a̲l̲i̲g̲n̲}̲ y=f(g(h(x)))=f…
然后把这些新变量作为节点,依据运算逻辑把公式整理出一张有向无环图(DAG)。即,原始函数建立计算图,数据正向传播,计算出中间节点xi,并记录计算图中的节点依赖关系。
因此,自动微分可以被认为是将一个复杂的数学运算过程分解为一系列简单的基本运算, 其中每一项基本运算都可以通过查表得出来。
2.2 计算模式
一般而言,存在两种不同的自动微分模式:
- 前向自动微分(Forward Automatic Differentiation,也叫做 tangent mode AD)或者前向累积梯度(前向模式)。
- 后向自动微分(Reverse Automatic Differentiation,也叫做 adjoint mode AD)或者说反向累计梯度(反向模式)。
两种自动微分模式都通过递归方式来求 dy/dx,只不过根据链式法则展开的形式不太一样。
前向梯度累积会指定从内到外的链式法则遍历路径,即先计算 d w 1 / d x d_{w1}/d_x dw1/dx,再计算 d w 2 / d w 1 d_{w2}/d_{w1} dw2/dw1,最后计算 d y / d w 2 dy/dw_2 dy/dw2,即,前向模式是在计算图前向传播的同时计算微分。因此前向模式的一次正向传播就可以计算出输出值和导数值。
d w i d x = d w i d w i − 1 d w i − 1 d x w i t h w 3 = y \frac{dw_i}{dx}=\frac{dw_i}{dw_{i-1}}\frac{dw_{i-1}}{dx} \qquad with\ w_3=y dxdwi=dwi−1dwidxdwi−1with w3=y
反向梯度累积正好相反,它会先计算 d y / d w 2 dy/dw_2 dy/dw2,然后计算 d w 2 / d w 1 d_{w2}/d_{w1} dw2/dw1,最后计算 d w 1 / d x d_{w1}/d_x dw1/dx。这是我们最为熟悉的反向传播模式,它非常符合「沿模型误差反向传播」这一直观思路。即,反向模式需要对计算图进行一次正向计算, 得出输出值,再进行反向传播。反向模式需要保存正向传播的中间变量值(比如 w i w_i wi),这些中间变量数值在反向传播时候被用来计算导数,所以反向模式的内存开销要大。
d y d w i = d y d w i + 1 d w i + 1 d w i w i t h w 0 = x \frac{dy}{dw_i} = \frac{dy}{dw_{i+1}}\frac{dw_{i+1}}{dw_i} \qquad with \ w_0 = x dwidy=dwi+1dydwidwi+1with w0=x
让我们再梳理一下:
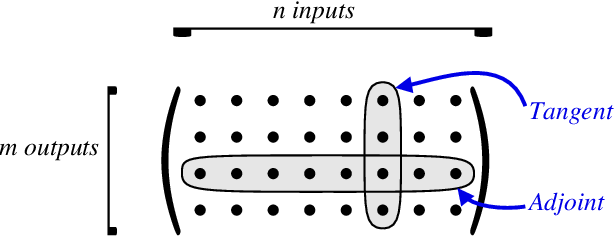
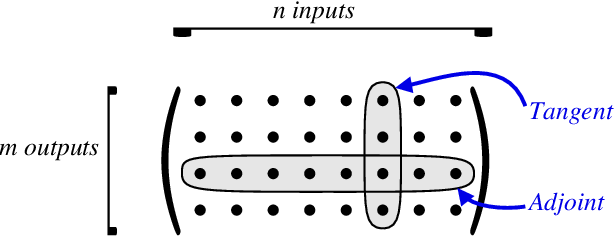
前向自动微分(tangent mode AD)和后向自动微分(adjoint mode AD)分别计算了Jacobian矩阵的一列和一行。(引自 [Hascoet2013])
前向自动微分(tangent mode AD)可以在一次程序计算中通过链式法则
∂ x k ∂ x j 0 = ∂ x k ∂ x k − 1 ∂ x k − 1 ∂ x j 0 \frac{∂x^k}{∂x^0_j} = \frac{∂x^k}{∂x^{k-1}} \frac{∂x^{k-1}}{∂x^0_j} ∂xj0∂xk=∂xk−1∂xk∂xj0∂xk−1
递推得到Jacobian矩阵中与单个输入有关的部分,或者说是Jacobian矩阵的一列。
后向自动微分(adjoint mode AD)利用链式法则
∂ x i L ∂ x k = ∂ x i L ∂ x k + 1 ∂ x k + 1 ∂ x k \frac{∂x^L_i}{∂x^k} = \frac{∂x^L_i}{∂x^{k+1}} \frac{∂x^{k+1}}{∂x^k} ∂xk∂xiL=∂xk+1∂xiL∂xk∂xk+1
可以仅通过一次对计算过程的遍历得到Jacobian矩阵的一行。但它的导数链式法则传递方向和程序执行方向相反,所以需要在程序计算过程中记录一些额外的信息来辅助求导,这些辅助信息包括计算图和计算过程的中间变量。
2.3 样例
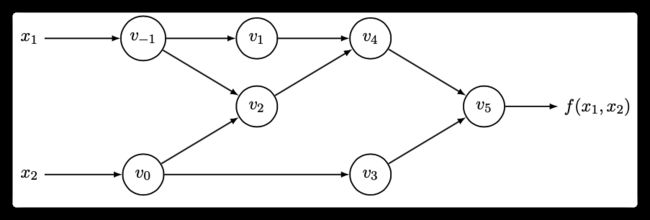
我们以公式 $ f(x_1, x_2) = ln(x_1) + x_1x_2 - sin(x_2)$ 为例,首先把它转换成一个计算图,则如下:
这里对于变量我们使用三段法表示:
-
输入变量 :自变量维度为 n,这里 n = 2,输入变量就是 x 1 , x 2 x_1, x_2 x1,x2 。
-
中间变量 :中间变量这里是 $v_{-1} $ 到 $ v_5$,在计算过程中,只需要针对这些中间变量做处理即可:将符号微分法应用于最基本的算子,然后代入数值,保留中间结果,最后再应用于整个函数。
-
输出变量 :假设输出变量维度为 m,这里 m = 1,输出变量就是 y 1 y_1 y1,也就是 f ( x 1 , x 2 ) f(x_1, x_2) f(x1,x2)。
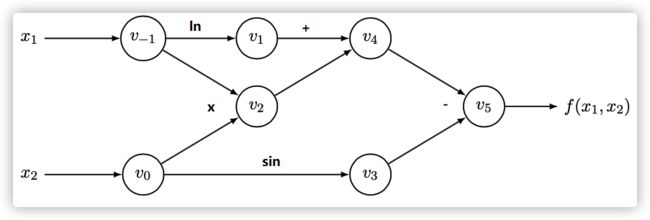
或者加上符号我们更容易理解。
转化成如上DAG(有向无环图)结构之后,我们可以很容易分步计算函数的值,并求取它每一步的导数值,然后,我们把 d f / d x 1 df / dx_1 df/dx1 求导过程利用链式法则表示成如下的形式:
可以看出整个求导可以被拆成一系列微分算子的组合。这里的计算可以分为两种:
- 将这个式子从前往后算的叫前向模式(Forward Mode)。
- 将这个式子从后往前算的叫逆向模式(Reverse Mode)。
2.4 前向模式(Forward Mode)
前向模式从计算图的起点开始,沿着计算图边的方向依次向前计算,最终到达计算图的终点。它根据自变量的值计算出计算图中每个节点的值 以及其导数值,并保留中间结果。一直得到整个函数的值和其导数值。整个过程对应于一元复合函数求导时从最内层逐步向外层求导。
2.4.1 计算过程
下面是前向模式的计算过程,下表中,左半部分是从左往右每个图节点的求值结果和计算过程,右半部分是每个节点对 x 1 x_1 x1的求导结果和计算过程。这里 V ˙ i \dot V_i V˙i 表示 V i V_i Vi 对 x 1 x_1 x1的偏导数。
我们给出一个推导分析,对于节点数值的计算如下:
- 我们给输入节点赋值: v − 1 = x 1 = 2 v_{-1} = x_1 = 2 v−1=x1=2, v 0 = x 2 = 5 v_{0} = x_2 = 5 v0=x2=5。
- 计算 v 1 v_1 v1节点: v 1 = l n v − 1 = l n x 1 = l n 2 v_1 = ln\ v_{-1} = ln\ x_1 = ln\ 2 v1=ln v−1=ln x1=ln 2 。
- 计算 v 2 v_2 v2 节点,节点 v_2 依赖于 v − 1 v_{-1} v−1 和 v 0 v_0 v0,即: v 2 = v − 1 × v 0 = x 1 × x 2 = 2 × 5 = 10 v_2=v_{−1} \times v_0=x_1 \times x_2= 2 \times 5 = 10 v2=v−1×v0=x1×x2=2×5=10
- 计算 v3 节点,$ v_3 = sin \ v_0 = sin \ 5$
- 计算 $ v_4 节 点 , 节点, 节点,v_4 = v_1 + v_2 = 0.693 + 10$
- 计算 v 5 v_5 v5节点, v 5 = v 1 + v 2 = 10.693 + 0.959 v_5 = v_1 + v_2 = 10.693 + 0.959 v5=v1+v2=10.693+0.959
- 最终 $ y = v_5 = 11.652$
此时,我们得到了图中所有节点的数值。而且在计算节点数值的同时,我们也一起计算导数,假设我们求 ∂ y ∂ x 1 \frac{∂y}{∂x_{1}} ∂x1∂y我们也是从输入计算。
-
v − 1 v_{-1} v−1 节点对于 x 1 x_1 x1梯度 : 因为 $v_{-1} = x_1 $,所以 ∂ v − 1 ∂ x 1 = 1 \frac{∂v_{-1}}{∂x{1}} = 1 ∂x1∂v−1=1
-
v 0 v_{0} v0 节点对于 x 1 x_1 x1梯度 : 因为 $v_{0} = x_2 $,这样就和 x 1 x_{1} x1 无关,所以 ∂ v 0 ∂ x 1 = 0 \frac{∂v_{0}}{∂x{1}} = 0 ∂x1∂v0=0
-
v 1 v_{1} v1 节点对于 x 1 x_1 x1梯度 : ∂ v 1 ∂ x 1 = ∂ l o g x 1 ∂ x 1 = 1 x 1 = 1 2 \frac{∂v_{1}}{∂x_{1}} = \frac{∂\ log \ x_1}{∂x_1} = \frac{1}{x_1} = \frac{1}{2} ∂x1∂v1=∂x1∂ log x1=x11=21
-
v 2 v_{2} v2 节点对于 x 1 x_1 x1梯度 : $\frac{∂v_{2}}{∂x_{1}} = \frac{∂v_{-1} }{∂x_1}\times v_0 + \frac{∂v_{0}}{ ∂x_1}\times v_{-1} = 1 \times 5 + 0 \times 2 $
-
v 3 v_{3} v3 节点对于 x 1 x_1 x1梯度 : ∂ v 0 ∂ x 1 × c o s v 0 = 0 × c o s 5 \frac{∂v_{0}}{∂x_{1}} \times cos \ v_0 = 0 \times cos \ 5 ∂x1∂v0×cos v0=0×cos 5
-
v 4 v_{4} v4 节点对于 x 1 x_1 x1梯度 : ∂ v 1 ∂ x 1 = ∂ v 1 ∂ x 1 + ∂ v 2 ∂ x 1 = 0.5 + 5 \frac{∂v_{1}}{∂x_{1}} = \frac{∂ v_1}{∂x_1} + \frac{∂ v_2}{∂x_1} = 0.5 + 5 ∂x1∂v1=∂x1∂v1+∂x1∂v2=0.5+5
-
v 5 v_{5} v5 节点对于 x 1 x_1 x1梯度 : ∂ v 1 ∂ x 1 = ∂ v 4 ∂ x 1 − ∂ v 3 ∂ x 1 = 5.5 − 0 \frac{∂v_{1}}{∂x_{1}} = \frac{∂v_4}{∂x_1} - \frac{∂v_3}{∂x_1} = 5.5 - 0 ∂x1∂v1=∂x1∂v4−∂x1∂v3=5.5−0
-
所以 ∂ y ∂ x 1 = ∂ v 5 ∂ x 1 = 5.5 \frac{∂y}{∂x_{1}} = \frac{∂v_5}{∂x_1} = 5.5 ∂x1∂y=∂x1∂v5=5.5
请注意:
- 计算图各个节点的数值和该节点的导数可同步求出。因为我们已经了解了深度学习,所以从深度学习角度来看,前向模式只需要完成计算出计算图中各节点的值。求导数则可以由反向模式来实现。
- 注意到每一步的求导都会利用到上一步的求导结果,这样不至于重复计算,因此也不会产生像符号微分法的"expression swell"问题。自动微分的前向模式实际上与我们在微积分里所学的求导过程一致。
3.4.2 推广
这个计算过程可以推广到雅克比矩阵,假设一个函数有 n 个输入变量 x i x_i xi,m个输入变量 y j y_j yj,即输入向量 x ∈ R n x∈R^n x∈Rn,而输出向量 y ∈ R m y∈R^m y∈Rm,则这个函数就是映射
f : R n → R m f : R ^n \rightarrow R^m f:Rn→Rm
在这种情况下,每个自动微分的前向传播计算时候,初始输入被设置为 x ˙ = 1 \dot{x} = 1 x˙=1,其余被设置为 0。
可以看出,一次前向计算,可以求出Jacobian矩阵的一列数据。比如 x 3 ˙ = 1 \dot{x_3} = 1 x3˙=1,对应就可以求出来第3列。
即,tangent mode AD可以在一次程序计算中通过链式法则递推得到Jacobian矩阵中与单个输入有关的部分,或者说是Jacobian矩阵的一列。如下图:
但是如果想求出来对所有输入 $x_i\ , , ,i = 1,…,n$ ,我们需要计算 n 次才能求出所有列。
进一步,通过设定 x ˙ = r \dot{x} = r x˙=r,我们可以在一次前向传播中直接计算 Jacobian–vector 乘积。
3.4.3 问题
前向模式的优点在于:实现起来很简单 [Revels2016],也不需要很多额外的内存空间。
前向模式的问题在于:
- 每次前向计算只能计算对一个自变量的偏导数,对于一元函数求导是高效的。但是机器学习模型的参数通常有 1 0 6 10^6 106数量级之多。
- 如果有一个函数,其输入有 n 个,输出有 m个,对于每个输入来说,前向模式都需要遍历计算过程以得到这个输入的导数,求解整个函数梯度需要 n 遍如上计算过程。尤其是神经网络这种 n ≫ m n \gg m n≫m 的模型,前向模式就太低效了,重复遍历计算过程 1 0 6 10^6 106次显然是无法接受的。
于是86年Hinton提出了用后向传播技术训练神经网络 [Rumelhart1986],也就是接下来要说的反向模式(adjoint mode AD)。
3.5 反向模式(Reverse Mode)
3.5.1 思路
后向自动微分是基于链式法则来工作。我们仅需要一个前向过程和反向过程就可以计算所有参数的导数或者梯度。因为需要结合前向和后向两个过程,因此反向自动微分会将所有的操作以一张图的方式存储下来,这张图就是计算图,计算图是一个有向无环图(DAG),它表达了函数和变量的关系。这是深度学习框架的核心之一:如何干净地产生一个计算图,随后再高效地计算它。
反向模式根据计算图从后(最后一个节点)向前计算,依次得到对每个中间变量节点的偏导数,直到到达自变量节点处,这样就得到了每个输入的偏导数。在每个节点处,根据该节点的后续节点(前向传播中的后续节点)计算其导数值。整个过程对应于多元复合函数求导时从最外层逐步向内侧求导。这样可以有效地把各个节点的梯度计算解耦开,每次只需要关注计算图中当前节点的梯度计算。
神经网络的backprop算法就是reverse mode自动微分的一种特殊形式。
从下图可以看出来,reverse mode和forward mode是一对相反过程,reverse mode从最终结果开始求导,利用最终输出对每一个节点进行求导。下图虚线就是反向模式。
3.5.2 计算过程
前向和后向两种模式的过程表达如下,表的左列浅色为前向计算函数值的过程,与前向计算时相同。右面列深色为反向计算导数值的过程。
需要注意的是:左列先计算,顺序是由上自下,右列后计算,顺序是由下往上。右图必须从下往上看,即,先计算输出 y 对节点 v 5 v_5 v5 的导数,用 v 5 ~ \tilde{v_5} v5~表示 ∂ y ∂ v 5 \frac{∂y}{∂v_5} ∂v5∂y,这样的记号可以强调我们对当前计算结果进行缓存,以便用于后续计算,而不必重复计算。
因为前向计算函数值得顺序与前向模式相同,所以我们不讨论,专注看看反向计算导数值的过程。为了更好的说明,我们在原图上插入数值和公式。
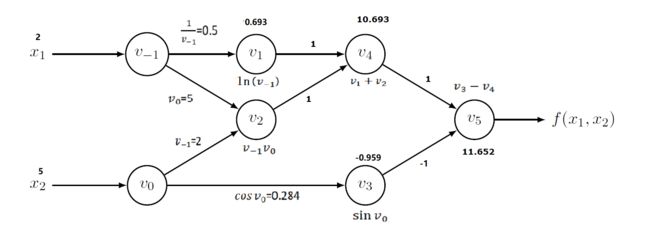
反向计算导数值时,顺序如下:
-
计算 y 对 v 5 v_5 v5的导数值,因为 $ y = v_5$, 所以 ∂ y ∂ v 5 = v 5 ′ = 1 \frac{∂y}{∂v_5} = v'_5 = 1 ∂v5∂y=v5′=1。
-
计算 y 对 v 4 v_4 v4的导数值,因为 v 4 v_4 v4 在图上只有一个后续节点 v 5 v_5 v5, 并且 v 5 = v 3 − v 4 v_5=v_3−v_4 v5=v3−v4,所以依据链式法则得到 ∂ y ∂ v 4 = ∂ y ∂ v 5 × ∂ v 5 ∂ v 4 = v 5 ′ ∂ v 5 ∂ v 4 = v 5 ′ ∂ ( v 3 − v 4 ) ∂ v 4 = v 5 ′ × 1 = 1 \frac{∂y}{∂v_4} =\frac{∂y}{∂v5} \times \frac{∂v5}{∂v4} = v'_5 \frac{∂v_5}{∂v_4} = v'_5 \frac{∂(v_3 - v_4)}{∂v_4} = v'_5 \times 1 = 1 ∂v4∂y=∂v5∂y×∂v4∂v5=v5′∂v4∂v5=v5′∂v4∂(v3−v4)=v5′×1=1,将结果写在 v 4 v_4 v4指向 v 5 v_5 v5的边上。
-
计算 y 对 v 3 v_3 v3的导数值,因为 v 3 v_3 v3 在图上只有一个后续节点 v 5 v_5 v5, 并且 v 5 = v 3 − v 4 v_5=v_3−v_4 v5=v3−v4,所以依据链式法则得到 ∂ y ∂ v 3 = ∂ y ∂ v 5 × ∂ v 5 ∂ v 3 = v 5 ′ ∂ v 5 ∂ v 3 = v 5 ′ ∂ ( v 3 − v 4 ) ∂ v 3 = v 5 ′ × ( − 1 ) = − 1 \frac{∂y}{∂v_3} =\frac{∂y}{∂v5} \times \frac{∂v5}{∂v3} = v'_5 \frac{∂v_5}{∂v_3} = v'_5 \frac{∂(v_3 - v_4)}{∂v_3} = v'_5 \times (-1) = -1 ∂v3∂y=∂v5∂y×∂v3∂v5=v5′∂v3∂v5=v5′∂v3∂(v3−v4)=v5′×(−1)=−1,,将结果写在 v 3 v_3 v3指向 v 5 v_5 v5的边上。
-
计算 y 对 v 1 v_1 v1的导数值,因为 v 1 v_1 v1 在图上只有一个后续节点 v 4 v_4 v4, 并且 v 4 = v 1 + v 2 v_4=v_1+v_2 v4=v1+v2,所以依据链式法则得到 ∂ y ∂ v 1 = ∂ y ∂ v 1 × ∂ v 4 ∂ v 1 = v 4 ′ ∂ v 4 ∂ v 1 = v 4 ′ ∂ ( v 1 + v 1 ) ∂ v 1 = v 4 ′ × 1 = 1 \frac{∂y}{∂v_1} =\frac{∂y}{∂v_1} \times \frac{∂v_4}{∂v_1} = v'_4 \frac{∂v_4}{∂v_1} = v'_4 \frac{∂(v_1 + v_1)}{∂v_1} = v'_4 \times 1 = 1 ∂v1∂y=∂v1∂y×∂v1∂v4=v4′∂v1∂v4=v4′∂v1∂(v1+v1)=v4′×1=1,,将结果写在 v 1 v_1 v1指向 v 4 v_4 v4的边上。
-
计算 y 对 v 2 v_2 v2的导数值,因为 v 2 v_2 v2 在图上只有一个后续节点 v 4 v_4 v4, 并且 v 4 = v 1 + v 2 v_4=v_1+v_2 v4=v1+v2,所以依据链式法则得到 ∂ y ∂ v 2 = ∂ y ∂ v 4 × ∂ v 4 ∂ v 2 = v 4 ′ ∂ v 4 ∂ v 2 = v 4 ′ ∂ ( v 1 + v 2 ) ∂ v 2 = v 4 ′ × 1 = 1 \frac{∂y}{∂v_2} =\frac{∂y}{∂v_4} \times \frac{∂v_4}{∂v_2} = v'_4 \frac{∂v_4}{∂v_2} = v'_4 \frac{∂(v_1 + v_2)}{∂v_2} = v'_4 \times 1 = 1 ∂v2∂y=∂v4∂y×∂v2∂v4=v4′∂v2∂v4=v4′∂v2∂(v1+v2)=v4′×1=1,,将结果写在 v 2 v_2 v2指向 v 4 v_4 v4的边上。
-
接下来要计算 y 对 v 0 v_0 v0的导数值 和 y 对 v − 1 v_{-1} v−1的导数值,因为 v 0 v_0 v0 和 v − 1 v_{-1} v−1 都是后续有两个节点,
- v 0 v_0 v0 在图上有两个后续节点 v 2 v_2 v2 和 v 3 v_3 v3, 并且 v 2 = v − 1 × v 0 v_2=v_{-1} \times v_0 v2=v−1×v0 和 v 3 = s i n v 0 v_3= sin \ v_0 v3=sin v0
- v − 1 v_{-1} v−1 在图上有两个后续节点 v 2 v_2 v2 和 v 1 v_1 v1, 并且 v 2 = v − 1 × v 0 v_2=v_{-1} \times v_0 v2=v−1×v0 和 v 1 = l n v − 1 v_1= ln \ v_{-1} v1=ln v−1
所以我们只能分开计算。
-
计算 ∂ v 3 ∂ v 0 = ∂ s i n v 0 ∂ v 0 = c o s v 0 = 0.284 \frac{∂v_3}{∂v_0} = \frac{∂sin\ v_0}{∂v_0} = cos\ v_0 = 0.284 ∂v0∂v3=∂v0∂sin v0=cos v0=0.284,将结果写在 v 0 v_0 v0指向 v 3 v_3 v3的边上。
-
计算 ∂ v 2 ∂ v 0 = ∂ ( v − 1 v 0 ) ∂ v 0 = v − 1 = 2 \frac{∂v_2}{∂v_0} = \frac{∂(v_{-1}v_0)}{∂v_0} = v_{-1} = 2 ∂v0∂v2=∂v0∂(v−1v0)=v−1=2,将结果写在 v 0 v_0 v0指向 v 2 v_2 v2的边上。
-
计算 ∂ v 2 ∂ v − 1 = ∂ ( v − 1 v 0 ) ∂ v − 1 = v 0 = 5 \frac{∂v_2}{∂v_{-1}} = \frac{∂(v_{-1}v_0)}{∂v_{-1}} = v_0 = 5 ∂v−1∂v2=∂v−1∂(v−1v0)=v0=5,将结果写在 v − 1 v_{-1} v−1指向 v 2 v_2 v2的边上。
-
计算 ∂ v 1 ∂ v − 1 = ∂ ( l n v − 1 ) ∂ v − 1 = 1 x 1 = 0.5 \frac{∂v_1}{∂v_{-1}} = \frac{∂(ln \ v_{-1})}{∂v_{-1}} = \frac{1}{x_1} = 0.5 ∂v−1∂v1=∂v−1∂(ln v−1)=x11=0.5,将结果写在 v − 1 v_{-1} v−1指向 v 1 v_1 v1的边上。
到目前为止,我们已经计算出来了所有步骤的偏导数的数值。现在需要计算 ∂ y ∂ x 1 \frac{∂y}{∂x_1} ∂x1∂y和 ∂ y ∂ x 2 \frac{∂y}{∂x_2} ∂x2∂y。计算 ∂ y ∂ x 1 \frac{∂y}{∂x_1} ∂x1∂y 就是从 y 开始从后向前走,走回到 x 1 x_1 x1,因为有多条路径,所以对于每一条路径,需要将这个路径上的数值连乘起来得到一个乘积数值,然后将这多条路径的乘积数值相加起来,就得到了 ∂ y ∂ x 1 \frac{∂y}{∂x_1} ∂x1∂y 的数值。 ∂ y ∂ x 2 \frac{∂y}{∂x_2} ∂x2∂y的计算方法与此相同。
从 y 到 x 1 x_1 x1 的路径有两条,分别是:
- v 5 → v 4 → v 1 → v − 1 v_5→v_4→v_1→v_{−1} v5→v4→v1→v−1 :其数值乘积是 1∗1∗0.5=0.5。
- v 5 → v 4 → v 2 → v − 1 v_5→v_4→v_2→v_{−1} v5→v4→v2→v−1 :其数值乘积是 1∗1∗ 5= 5。
因此,$\frac{∂y}{∂x_1} = 0.5 + 5 = 5.5 $
从 y 到 x 2 x_2 x2 的路径有两条,分别是:
- v 5 → v 4 → v 2 → v 0 v_5→v_4→v_2→v_0 v5→v4→v2→v0 :其数值乘积是 1∗1∗2=2.0。
- v 5 → v 3 → v 0 v_5→v_3→v_0 v5→v3→v0 :其数值乘积是 (−1)∗0.284=−0.284。
因此,$\frac{∂y}{∂x_1} = 2.0+(−0.284)=1.716 $
3.5.3 推广
如果要同时计算多个变量的偏导数,则可以借助雅克比矩阵完成。假设一个函数有 n 个输入变量 x i x_i xi,m个输入变量 y j y_j yj,即输入向量 x ∈ R n x∈R^n x∈Rn,而输出向量 y ∈ R m y∈R^m y∈Rm,则这个函数就是映射
f : R n → R m f : R ^n \rightarrow R^m f:Rn→Rm
得到雅克比矩阵是:
即通过雅克比矩阵转置与后续节点梯度值的乘积,可以得到当前节点的梯度值。
3.5.4 内存问题和inplace 操作
前向模式在计算之中,计算图各个节点的数值和该节点的导数可同步求出,但是代价就是对于多个输入需要多次计算才行。而反向模式可以通过一次反向传输,就计算出所有偏导数,而且中间的偏导数计算只需计算一次,减少了重复计算的工作量,在多参数的时候后向自动微分的时间复杂度更低,但这是以增加存储量需求为代价的。
因为在反向计算时需要寻找它所有的后续节点,收集这些节点的导数值,然后计算本节点的导数值。整个计算过程中不仅利用了每个节点的后续节点的导数值 ∂ f ∂ v n j \frac{∂f}{∂v_{n_j}} ∂vnj∂f ,还需要利用某些节点的函数值以计算 ∂ v n j ∂ v i \frac{∂v_{n_j}}{∂v_i} ∂vi∂vnj,因此需要在前向计算时保存所有节点的值,供反向计算使用,不必重复计算。
因为反向模式的特点带来了大量内存占用,为了减少内存操作,各个深度学习框架做了很多优化,也带来了很多限制。比如 PyTorch 的求导就不支持绝大部分 inplace 操作。
inplace 指的是在不更改变量的内存地址的情况下,直接修改变量的值。
# 情景 1,不是 inplace,类似 Python 中的 `i=i+1`
a = a.exp()
# 情景 2,是 inplace 操作,类似 `i+=1`
a[0] = 10
为什么不支持,因为如果变量 A 已经参与了正向传播计算,然后它的数值被修改了。但接下来反向传播时候怎么办?反向传播用这个新 A 值肯定是不正确的。但是从哪里去找修改之前的值呢?
一个办法是对于每个变量(因为无法确定哪个变量可能被修改)在做前向传播计算之后,都开辟新的空间来保存这个变量数值,这样以后无论怎么修改都不怕了。但是这样会导致内存剧增。所以只能限制 inplace 操作。
3.6 比较
如下图所示,前向自动微分(tangent mode AD和后向自动微分(adjoint mode AD)分别计算了Jacobian矩阵的一列和一行。(引自 [Hascoet2013])
从矩阵乘法次数的角度来看,前向模式和反向模式的不同之处在于矩阵相乘的起始之处不同。
正向,反向两种模式算的梯度值是一样的,但因为计算顺序不同,所以计算速度有差异。
当输出维度小于输入维度,反向模式的乘法次数要小于前向模式。因此,当输出的维度大于输入的时候,适宜使用前向模式微分;当输出维度远远小于输入的时候,适宜使用反向模式微分。即,后向自动微分更加适合多参数的情况,多参数的时候后向自动微分的时间复杂度更低,只需要一遍reverse mode的计算过程,便可以求出输出对于各个输入的导数,从而轻松求取梯度用于后续优化更新。
0x04 PyTorch
我们接下来大体看看 PyTorch 的自动微分,为后续分析打下基础。
4.1 原理
PyTorch 反向传播的计算主要是通过autograd类实现了自动微分功能,而autograd 的基础是:
- 数学基础:复合函数,链式求导法则和雅克比矩阵;
- 工程基础 :Tensor 构成的计算图(DAG有向无环图);
4.1.1 雅克比矩阵
在数学上,如果你有一个向量值函数 y ⃗ = f ( x ⃗ ) \vec{y}=f(\vec{x}) y=f(x) ,那么梯度 y ⃗ \vec{y} y 关于 x ⃗ \vec{x} x 的梯度是一个雅可比矩阵 J,雅可比矩阵 J 包含以下所有偏导组合:
J = [ ∂ f ∂ x 1 . . . ∂ f ∂ x n ] = { ∂ f 1 ∂ x 1 ⋯ ∂ f 1 ∂ x n ⋮ ⋱ ⋮ ∂ f m ∂ x 1 ⋯ ∂ f m ∂ x n } J = [\frac{∂f}{∂x_1} ... \frac{∂f}{∂x_n}] = \left\{ \begin{matrix} \frac{∂f_1}{∂x_1} & \cdots & \frac{∂f_1}{∂x_n}\\ \vdots & \ddots & \vdots \\ \frac{∂f_m}{∂x_1} & \cdots & \frac{∂f_m}{∂x_n} \end{matrix} \right\} J=[∂x1∂f...∂xn∂f]=⎩⎪⎨⎪⎧∂x1∂f1⋮∂x1∂fm⋯⋱⋯∂xn∂f1⋮∂xn∂fm⎭⎪⎬⎪⎫
或者是:
J = ( ∂ y ∂ x 1 . . . ∂ y ∂ x n ) = ( ∂ y 1 ∂ x 1 ⋯ ∂ y 1 ∂ x n ⋮ ⋱ ⋮ ∂ y m ∂ x 1 ⋯ ∂ y m ∂ x n ) J = \left(\begin{array}{cc} \frac{\partial \bf{y}}{\partial x_{1}} & ... & \frac{\partial \bf{y}}{\partial x_{n}} \end{array}\right) = \left(\begin{array}{ccc} \frac{\partial y_{1}}{\partial x_{1}} & \cdots & \frac{\partial y_{1}}{\partial x_{n}}\\ \vdots & \ddots & \vdots\\ \frac{\partial y_{m}}{\partial x_{1}} & \cdots & \frac{\partial y_{m}}{\partial x_{n}} \end{array}\right) J=(∂x1∂y...∂xn∂y)=⎝⎜⎛∂x1∂y1⋮∂x1∂ym⋯⋱⋯∂xn∂y1⋮∂xn∂ym⎠⎟⎞
上面的矩阵表示f(X)相对于X的梯度。注意:雅可比矩阵实现的是 n 维向量 到 m 维向量的映射。
我们下面看看 PyTorch 的思路。
backward 函数
在现实中,PyTorch 是使用backward函数进行反向求导。
def backward(self, gradient=None,...)
backward 方法根据gradient参数的不同有2种可能:
- 如果gradient 是标量,我们可以直接计算完整的雅克比矩阵。如果缺省则使用默认值 1,即 backward(torch.tensor(1.))。
- 如果 gradient 是向量 vector。PyTorch 不会显式构造整个雅可比矩阵(实际的梯度),而是直接计算 Jacobian 乘积(Jacobian vector product),这通常更简单有效,而且存储真正的梯度会浪费大量空间。
torch.autograd 类
backward 方法最终调用的是torch.autograd 类。在 PyTorch 之中,torch.autograd 类从数学来说就是一个雅可比向量积计算引擎。
我们假设如下:一个启用梯度的张量X, X = [ x 1 , x 2 , … , x n ] X = [x_1,x_2,…,x_n] X=[x1,x2,…,xn], 假设这是某个机器学习模型的权值。X 经过一些运算形成一个向量 Y , Y = f ( X ) = [ y 1 , y 2 , … , y m ] Y = f(X) = [y_1, y_2,…,y_m] Y=f(X)=[y1,y2,…,ym]。然后使用Y计算标量损失l。假设向量 v 恰好是标量损失 l 关于向量 Y 的梯度,则向量 v 称为**grad_tensor(梯度张量)**,
对于一个向量输入 v ⃗ \vec{v} v,backward方法计算的是 $ J^{T}\cdot \vec{v}$ 。参数 grad_tensor 就是这里的 v,需要与 Tensor 本身有相同的size。如果 v ⃗ \vec{v} v 恰好是标量函数的梯度 l = g ( y ⃗ ) l=g\left(\vec{y}\right) l=g(y),即当gradient为标量时候,
v ⃗ = ( ∂ l ∂ y 1 ⋯ ∂ l ∂ y m ) T \vec{v} = \left(\begin{array}{ccc}\frac{\partial l}{\partial y_{1}} & \cdots & \frac{\partial l}{\partial y_{m}}\end{array}\right)^{T} v=(∂y1∂l⋯∂ym∂l)T
损失函数 l = g ( y ⃗ ) l=g\left(\vec{y}\right) l=g(y) 是一个从向量 y ⃗ \vec{y} y 到标量 l 的映射,那么 l 对于 y 的梯度是 ( ∂ l ∂ y 1 . . . ∂ l ∂ y m ) (\frac{∂l}{∂y_1} ... \frac{∂l}{∂y_m}) (∂y1∂l...∂ym∂l)。根据链式法则, l = g ( y ⃗ ) l = g(\vec{y}) l=g(y) 和 y ⃗ = f ( x ⃗ ) \vec{y} = f(\vec{x}) y=f(x) 则标量 l 关于 x ⃗ \vec{x} x的梯度就是 向量-雅可比积:
J T ⋅ v ⃗ = ( ∂ y 1 ∂ x 1 ⋯ ∂ y m ∂ x 1 ⋮ ⋱ ⋮ ∂ y 1 ∂ x n ⋯ ∂ y m ∂ x n ) ( ∂ l ∂ y 1 ⋮ ∂ l ∂ y m ) = ( ∂ l ∂ x 1 ⋮ ∂ l ∂ x n ) J^{T}\cdot \vec{v}=\left(\begin{array}{ccc} \frac{\partial y_{1}}{\partial x_{1}} & \cdots & \frac{\partial y_{m}}{\partial x_{1}}\\ \vdots & \ddots & \vdots\\ \frac{\partial y_{1}}{\partial x_{n}} & \cdots & \frac{\partial y_{m}}{\partial x_{n}} \end{array}\right)\left(\begin{array}{c} \frac{\partial l}{\partial y_{1}}\\ \vdots\\ \frac{\partial l}{\partial y_{m}} \end{array}\right)=\left(\begin{array}{c} \frac{\partial l}{\partial x_{1}}\\ \vdots\\ \frac{\partial l}{\partial x_{n}} \end{array}\right) JT⋅v=⎝⎜⎛∂x1∂y1⋮∂xn∂y1⋯⋱⋯∂x1∂ym⋮∂xn∂ym⎠⎟⎞⎝⎜⎛∂y1∂l⋮∂ym∂l⎠⎟⎞=⎝⎜⎛∂x1∂l⋮∂xn∂l⎠⎟⎞
这种计算雅可比矩阵并将其与向量v相乘的方法使PyTorch能够轻松地为非标量输出提供外部梯度。
4.1.2 计算图
前面提到过,训练分几步执行:
- 原始函数建立计算图,将问题转化成一种有向无环图。
- 进行正向传播,计算出中间节点,并记录计算图中的节点依赖关系。
- 反向传播,从输出开始遍历计算图,计算输出对于每个节点的导数。
可以看出来,计算图是这里的关键,是自动微分的工程基础。计算图就是用图的方式来表示计算过程,每一个数据都是计算图的一个节点,数据之间的计算即流向关系由节点之间的边来表示。它将多输入的复杂计算表达成了由多个基本二元计算组成的有向图,并保留了所有中间变量,这种结构天然适用于利用链式法则进行自动求导,可以完全向用户隐藏求导过程。
比如该图所表示的运算为 ( a + b ) × c (a+b) \times c (a+b)×c。其中节点 v 1 v_1 v1 表示中间结果, v 2 v_2 v2 表示最终结果。计算图的一个核心特征是可以通过传递"局部计算”来获得最终结果。
深度学习框架中,底层结构都是由张量组成的计算图,当然PyTorch在实际前向传播过程中,并没有显示地构造出计算图,但是其计算路径的确是沿着计算图的路径来进行,而向后图是由autograd类在向前传递过程中自动动态创建的。
4.1.3 神经网络中的链式法则
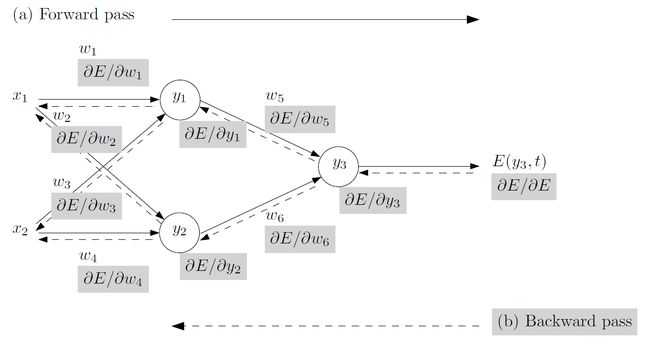
下面我们看一个简单的神经网络模型中链式求导法则应用的例子,摘录自 https://blog.paperspace.com/pytorch-101-understanding-graphs-and-automatic-differentiation/:
某神经网络中有5个神经元,其中 w 1 w_1 w1至 w 4 w_4 w4 是权重矩阵,L 是输出,其计算关系如下:
b = w 1 ∗ a c = w 2 ∗ a d = w 3 ∗ b + w 4 ∗ c L = 10 − d b=w_1∗a \\ c=w_2∗a\\ d=w_3∗b+w_4∗c\\ L=10−d b=w1∗ac=w2∗ad=w3∗b+w4∗cL=10−d
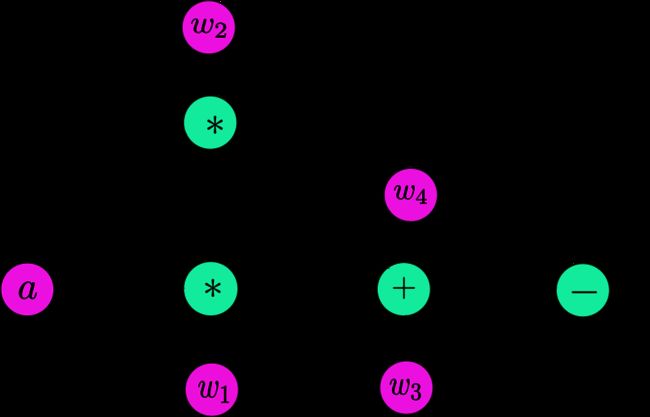
则其组成的前向计算图如下:
其求导规则是:
$$
\frac{∂L}{∂w_4} = \frac{\partial{L}}{\partial{d}} * \frac{\partial{d}}{\partial{w_4}}\
\frac{\partial{L}}{\partial{w_3}} = \frac{\partial{L}}{\partial{d}} * \frac{\partial{d}}{\partial{w_3}} \
\frac{\partial{L}}{\partial{w_2}} = \frac{\partial{L}}{\partial{d}} * \frac{\partial{d}}{\partial{c}} * \frac{\partial{c}}{\partial{w_2}} \
\frac{\partial{L}}{\partial{w_1}} = \frac{\partial{L}}{\partial{d}} * \frac{\partial{d}}{\partial{b}} * \frac{\partial{b}}{\partial{w_1}}
$$
对应如下图:
在pytorch中,反向传播计算过程就和上图类似。
比如,如果计算 L 对 w2 的偏导,就是按照如下计算图的路径:
∂ L ∂ w 2 = ∂ L ∂ d ∗ ∂ d ∂ c ∗ ∂ c ∂ w 2 \frac{\partial{L}}{\partial{w_2}} = \frac{\partial{L}}{\partial{d}} * \frac{\partial{d}}{\partial{c}} * \frac{\partial{c}}{\partial{w_2}} \\ ∂w2∂L=∂d∂L∗∂c∂d∗∂w2∂c
即,先求 L 对于 d 的偏导数,再求 d 对 c 的偏导数,再求 c 对 w 2 w_2 w2 的偏导数,最后把所有乘起来,就是最终答案。
另外,雅克比矩阵可表示所有L对所有权重的偏导:
J = [ ∂ L ∂ w 1 , ∂ L ∂ w 2 , ∂ L ∂ w 3 , ∂ L ∂ w 4 ] J = [\frac{\partial{L}}{\partial{w_1}}, \frac{\partial{L}}{\partial{w_2}}, \frac{\partial{L}}{\partial{w_3}}, \frac{\partial{L}}{\partial{w_4}}] J=[∂w1∂L,∂w2∂L,∂w3∂L,∂w4∂L]
反向传播过程中一般用来传递上游传来的梯度,从而实现链式法则。
I可以表示损失函数,y表示输出,x表示中间的数据或者权重参数。中间层可以类比,每一层都可以看做是一个雅克比矩阵,v可能就是一个矩阵了。通过迭代可以求得loss对任意参数的导数。
雅克比矩阵的这个特点使得将外部梯度输入到一个带有非标量输出的模型变得非常简单。
4.2 PyTorch 功能
PyTorch 有两种求导方法。
4.2.1 方法1 backward
backward 是 通过 torch.autograd.backward()求导。具体定义如下:
def backward(self, gradient=None, retain_graph=None, create_graph=False, inputs=None):
r"""
Args:
gradient (Tensor or None): Gradient w.r.t. the
tensor. If it is a tensor, it will be automatically converted
to a Tensor that does not require grad unless ``create_graph`` is True.
None values can be specified for scalar Tensors or ones that
don't require grad. If a None value would be acceptable then
this argument is optional.
retain_graph (bool, optional): If ``False``, the graph used to compute
the grads will be freed. Note that in nearly all cases setting
this option to True is not needed and often can be worked around
in a much more efficient way. Defaults to the value of
``create_graph``.
create_graph (bool, optional): If ``True``, graph of the derivative will
be constructed, allowing to compute higher order derivative
products. Defaults to ``False``.
inputs (sequence of Tensor): Inputs w.r.t. which the gradient will be
accumulated into ``.grad``. All other Tensors will be ignored. If not
provided, the gradient is accumulated into all the leaf Tensors that were
used to compute the attr::tensors. All the provided inputs must be leaf
Tensors.
"""
if has_torch_function_unary(self):
return handle_torch_function(
Tensor.backward,
(self,),
self,
gradient=gradient,
retain_graph=retain_graph,
create_graph=create_graph,
inputs=inputs)
torch.autograd.backward(self, gradient, retain_graph, create_graph, inputs=inputs)
其参数为:
gradient: 如果张量是非标量(即其数据有多个元素)且需要梯度,则backward函数还需要指定“梯度”。它应该是类型和位置都匹配的张量。retain_graph: 如果设置为False,用于计算梯度的图形将被释放。通常在调用backward后,会自动把计算图销毁,如果要想对某个变量重复调用backward,需要将该参数设置为True。create_graph: 当设置为True的时候可以用来计算更高阶的梯度。inputs:需要计算梯度的张量。如果没有提供,则梯度被累积到所有叶子张量上。
需要注意的是,这个函数只是提供求导功能,并不返回值,返回的总是None。
简单的自动求导
如果Tensor类表示的是一个标量(即它包含一个元素的张量),则不需要为backward()指定任何参数。
a = torch.tensor(1.0, requires_grad=True)
b = torch.tensor(2.0, requires_grad=True)
z = x**3+b
z.backward()
print(z, a.grad, b.grad)
输出
tensor([ 8., 10., 12.])
tensor([147., 192., 243.])
如果使用inputs参数,比如:
torch.autograd.backward([z], inputs=[a])
则只会在 a 上累积,b上不会计算梯度。
复杂的自动求导
但是如果需要计算梯度的Tensor类有更多的元素,即张量是一个向量或者是一个矩阵,则需要指定一个gradient参数,它是形状匹配的张量,比如:
import torch
x = torch.randn(2, 2, dtype=torch.double, requires_grad=True)
y = torch.randn(2, 2, dtype=torch.double, requires_grad=True)
def fn():
return x ** 2 + y * x + y ** 2
gradient = torch.ones(2, 2)
torch.autograd.backward(fn(), gradient, inputs=[x, y])
print(x.grad)
print(y.grad)
输出
tensor([[-1.0397, -2.4018],
[-0.5114, 0.2455]], dtype=torch.float64)
tensor([[-0.9240, -2.5764],
[-1.4938, 1.2254]], dtype=torch.float64)
4.2.2 方法2 grad
方法二是通过torch.autograd.grad()来求导。该函数会自动完成求导过程,而且会自动返回对于每一个自变量求导的结果。这是和backward不一样的地方。
具体定义如下:
def grad(
outputs: _TensorOrTensors,
inputs: _TensorOrTensors,
grad_outputs: Optional[_TensorOrTensors] = None,
retain_graph: Optional[bool] = None,
create_graph: bool = False,
only_inputs: bool = True,
allow_unused: bool = False
) -> Tuple[torch.Tensor, ...]:
r"""Computes and returns the sum of gradients of outputs with respect to
the inputs.
``grad_outputs`` should be a sequence of length matching ``output``
containing the "vector" in Jacobian-vector product, usually the pre-computed
gradients w.r.t. each of the outputs. If an output doesn't require_grad,
then the gradient can be ``None``).
If ``only_inputs`` is ``True``, the function will only return a list of gradients
w.r.t the specified inputs. If it's ``False``, then gradient w.r.t. all remaining
leaves will still be computed, and will be accumulated into their ``.grad``
attribute.
.. note::
If you run any forward ops, create ``grad_outputs``, and/or call ``grad``
in a user-specified CUDA stream context, see
:ref:`Stream semantics of backward passes`.
Args:
outputs (sequence of Tensor): outputs of the differentiated function.
inputs (sequence of Tensor): Inputs w.r.t. which the gradient will be
returned (and not accumulated into ``.grad``).
grad_outputs (sequence of Tensor): The "vector" in the Jacobian-vector product.
Usually gradients w.r.t. each output. None values can be specified for scalar
Tensors or ones that don't require grad. If a None value would be acceptable
for all grad_tensors, then this argument is optional. Default: None.
retain_graph (bool, optional): If ``False``, the graph used to compute the grad
will be freed. Note that in nearly all cases setting this option to ``True``
is not needed and often can be worked around in a much more efficient
way. Defaults to the value of ``create_graph``.
create_graph (bool, optional): If ``True``, graph of the derivative will
be constructed, allowing to compute higher order derivative products.
Default: ``False``.
allow_unused (bool, optional): If ``False``, specifying inputs that were not
used when computing outputs (and therefore their grad is always zero)
is an error. Defaults to ``False``.
"""
outputs = (outputs,) if isinstance(outputs, torch.Tensor) else tuple(outputs)
inputs = (inputs,) if isinstance(inputs, torch.Tensor) else tuple(inputs)
overridable_args = outputs + inputs
if has_torch_function(overridable_args):
return handle_torch_function(
grad,
overridable_args,
outputs,
inputs,
grad_outputs=grad_outputs,
retain_graph=retain_graph,
create_graph=create_graph,
only_inputs=only_inputs,
allow_unused=allow_unused,
)
if not only_inputs:
warnings.warn("only_inputs argument is deprecated and is ignored now "
"(defaults to True). To accumulate gradient for other "
"parts of the graph, please use torch.autograd.backward.")
grad_outputs_ = _tensor_or_tensors_to_tuple(grad_outputs, len(outputs))
grad_outputs_ = _make_grads(outputs, grad_outputs_)
if retain_graph is None:
retain_graph = create_graph
return Variable._execution_engine.run_backward(
outputs, grad_outputs_, retain_graph, create_graph,
inputs, allow_unused, accumulate_grad=False)
参数如下:
outputs: 结果节点,微分函数的输出,即需要求导的那个函数。inputs: 叶子节点,即返回的梯度,即函数的自变量。grad_outputs: Jacobian-vector 积中的向量。retain_graph: 如果设置为False,用于计算梯度的图形将被释放。通常在调用backward后,会自动把计算图销毁,如果要想对某个变量重复调用backward,需要将该参数设置为True。create_graph: 当设置为True的时候可以用来计算更高阶的梯度。allow_unused: 默认为False, 即必须要指定input,如果没有指定的话则报错。
例子如下:
import torch
x = torch.randn(2, 2, requires_grad=True)
y = torch.randn(2, 2, requires_grad=True)
z = x ** 2 + y * x + y ** 2
z.backward(torch.ones(2, 2), create_graph=True)
x_grad = 2 * x + y
y_grad = x + 2 * y
grad_sum = 2 * x.grad + y.grad
x_hv = torch.autograd.grad(
outputs=[grad_sum], grad_outputs=[torch.ones(2, 2)],
inputs=[x], create_graph=True)
print(x.grad)
print(y.grad)
输出
tensor([[ 2.3553, -1.9640],
[ 0.5467, -3.1051]], grad_fn=)
tensor([[ 1.8319, -2.8185],
[ 0.5835, -2.5158]], grad_fn=)
4.3 模拟印证
接下来,我们用 PyTorch 代码来大致模拟印证一下自动微分的过程。
4.3.1 原始版本
以下是原始版本,就是直接用一个公式来计算出梯度。
import torch
x1 = torch.tensor(2., requires_grad=True)
x2 = torch.tensor(5., requires_grad=True)
y = torch.log(x1) + x1 * x2 - torch.sin(x2)
grads = torch.autograd.grad(y, [x1, x2])
print('y is :', y)
print('grad is : ', grads[0],grads[1]) #
输出为如下,其中 grads[0],grads[1] 分别是y 对于 x1 和 x2 的梯度。
y is : tensor(11.6521, grad_fn=<SubBackward0>)
grad is : tensor(5.5000) tensor(1.7163)
4.3.2 前向模式
下面我们看看前向模式的大致模拟,我们把中间计算用变量表示出来,其中 dv1~dv4 就是梯度。
可以看到在前向过程中的变量数值和梯度数值,大家可以和前面推导的计算过程印证看看。
import torch
x1 = torch.tensor(2., requires_grad=True)
x2 = torch.tensor(5., requires_grad=True)
v1 = torch.log(x1)
v2 = x1 * x2
v3 = torch.sin(x2)
v4 = v1 + v2
y = v4 - v3
dv1 = torch.autograd.grad(v1, [x1], retain_graph=True)
dv2 = torch.autograd.grad(v2, [x1], retain_graph=True)
dv3 = torch.autograd.grad(v3, [x2], retain_graph=True)
dv4 = torch.autograd.grad(v4, [x1, x2], retain_graph=True)
grads = torch.autograd.grad(y, [x1, x2])
print('v1 is :', v1)
print('v2 is :', v2)
print('v3 is :', v3)
print('v4 is :', v4)
print('y is :', y)
print('dv1 is :', dv1)
print('dv2 is :', dv2)
print('dv3 is :', dv3)
print('dv4 is :', dv4)
print('grad is : ', grads[0],grads[1])
输出是:
v1 is : tensor(0.6931, grad_fn=<LogBackward>)
v2 is : tensor(10., grad_fn=<MulBackward0>)
v3 is : tensor(-0.9589, grad_fn=<SinBackward>)
v4 is : tensor(10.6931, grad_fn=<AddBackward0>)
y is : tensor(11.6521, grad_fn=<SubBackward0>)
dv1 is : (tensor(0.5000),)
dv2 is : (tensor(5.),)
dv3 is : (tensor(0.2837),)
dv4 is : (tensor(5.5000), tensor(2.))
grad is : tensor(5.5000) tensor(1.7163)
4.3.3 反向模式
下面我们看看反向模式的大致模拟,我们把中间计算用变量表示出来,其中 dv系列变量就是梯度。
可以看到在反向过程中的变量数值和梯度数值,大家可以和前面推导的计算过程印证看看。
import torch
x1 = torch.tensor(2., requires_grad=True)
x2 = torch.tensor(5., requires_grad=True)
v1 = torch.log(x1)
v2 = x1 * x2
v3 = torch.sin(x2)
v4 = v1 + v2
y = v4 - v3
dv4 = torch.autograd.grad(y, [v4], retain_graph=True)
dv3 = torch.autograd.grad(y, [v3], retain_graph=True)
dv2 = torch.autograd.grad(v4, [v2], retain_graph=True)
dv1 = torch.autograd.grad(v4, [v1], retain_graph=True)
dv0 = torch.autograd.grad(v3, [x2], retain_graph=True)
dv21 = torch.autograd.grad(v2, [x1], retain_graph=True)
dv22 = torch.autograd.grad(v2, [x2], retain_graph=True)
dv11 = torch.autograd.grad(v1, [x1], retain_graph=True)
grads = torch.autograd.grad(y, [x1, x2])
print('v1 is :', v1)
print('v2 is :', v2)
print('v3 is :', v3)
print('y is :', y)
print('dv4 is :', dv4)
print('dv3 is :', dv3)
print('dv2 is :', dv2)
print('dv1 is :', dv1)
print('dv0 is :', dv0)
print('dv21 is :', dv21)
print('dv22 is :', dv22)
print('dv11 is :', dv11)
print('grad is : ', grads[0],grads[1])
输出是
v1 is : tensor(0.6931, grad_fn=<LogBackward>)
v2 is : tensor(10., grad_fn=<MulBackward0>)
v3 is : tensor(-0.9589, grad_fn=<SinBackward>)
y is : tensor(11.6521, grad_fn=<SubBackward0>)
dv4 is : (tensor(1.),)
dv3 is : (tensor(-1.),)
dv2 is : (tensor(1.),)
dv1 is : (tensor(1.),)
dv0 is : (tensor(0.2837),)
dv21 is : (tensor(5.),)
dv22 is : (tensor(2.),)
dv11 is : (tensor(0.5000),)
grad is : tensor(5.5000) tensor(1.7163)
0xEE 个人信息
★★★★★★关于生活和技术的思考★★★★★★
微信公众账号:罗西的思考
如果您想及时得到个人撰写文章的消息推送,或者想看看个人推荐的技术资料,敬请关注。
![]()
0xFF 参考
https://blog.paperspace.com/pytorch-101-understanding-graphs-and-automatic-differentiation/
Yann LeCun:深度学习已死,可微分编程万岁!
自动微分技术
TensorFlow可微编程实践2—自动微分符号体系
https://en.wikipedia.org/wiki/Automatic_differentiation
Pytorch学习2020春-1-线性回归
自动微分(Automatic Differentiation)
自动微分(Automatic Differentiation)简介——tensorflow核心原理
浅谈 PyTorch 中的 tensor 及使用
【深度学习之美01】什么是(机器/深度)学习?
【深度学习之美15】如何感性认识损失函数?
【深度学习之美18】到底什么是梯度?
【深度学习之美21】BP算法详解之前向传播
【深度学习之美22】BP算法详解之链式法则
【深度学习之美23】BP算法详解之反向传播
【深度学习理论】一文搞透梯度下降Gradient descent
梯度下降算法(Gradient Descent)的原理和实现步骤
梯度下降方法与求导
【深度学习理论】纯公式手推+代码撸——神经网络的反向传播+梯度下降
深度学习—反向传播的具体案例
神经网络中 BP 算法的原理与 Python 实现源码解析
机器学习之——自动求导
Automatic Differentiation in Machine Learning: a Survey, https://arxiv.org/pdf/1502.05767.pdf
人工智能引擎——自动微分
自动微分(Automatic Differentiation)简介
The Autodiff Cookbook
Automatic Differentiation in Machine Learning: a Survey
自动微分(Automatic Differentiation)简介
PyTorch 的 backward 为什么有一个 grad_variables 参数?
自动微分到底是什么?这里有一份自我简述
BACKPACK: PACKING MORE INTO BACKPROP
深度 | 从概念到实践,我们该如何构建自动微分库
梯度下降是最好的程序员:Julia未来将内嵌可微编程系统
自动微分技术
微分编程(一):传统自动微分的三宗罪
一天实现自己的自动微分
【深度学习理论】一文搞透pytorch中的tensor、autograd、反向传播和计算图
PyTorch自动微分基本原理
[PyTorch 学习笔记] 1.5 autograd 与逻辑回归
PyTorch 的 Autograd
OpenMMLab:PyTorch 源码解读之 torch.autograd:梯度计算详解
https://zhuanlan.zhihu.com/p/348555597)
AI 框架基础技术之自动求导机制 (Autograd)
自动微分(Automatic Differentiation)简介
[12] Laurent Hascoet and Valérie Pascual. The tapenade automatic differentiation tool: Principles, model, and specification. ACM Transactions on Mathematical Software (TOMS), 39(3):20, 2013.
TensorFlow可微编程实践1—自动微分简介
TensorFlow可微编程实践2—自动微分符号体系
https://zhuanlan.zhihu.com/p/163892899