群智能算法(遗传算法, 粒子群算法, 蚁群算法原理与实例分析)
群智能算法:遗传算法, 粒子群算法, 蚁群算法的原理与实例分析
- 1. 问题重述
-
- 1.1 解决步骤
- 1.2 问题粗析
- 2. 遗传算法求解
-
- 2.1 步骤
- 2.2 结果
- 2.3 结果分析
- 2.4 遗传算法小结
- 3. 粒子群算法求解
-
- 3.1 步骤
- 3.2 结果
- 3.3 结果分析
- 3.4 小结
解决函数极值问题(二元), 采用三种群智能算法实现, 并进行比较分析
1. 问题重述
求解函数: f ( x , y ) = 6.452 ( x + 0.125 y ) ( cos x − cos ( 2 y ) ) 2 0.8 + ( x − 4.2 ) 2 + 2 ( y − 7 ) 2 + 3.226 y f(x, y)=\frac{6.452(x+0.125 y)(\cos x-\cos (2 y))^{2}}{\sqrt{0.8+(x-4.2)^{2}+2(y-7)^{2}}}+3.226 y f(x,y)=0.8+(x−4.2)2+2(y−7)26.452(x+0.125y)(cosx−cos(2y))2+3.226y的最大值, 其中 x ∈ [ 0 , 10 ) , y ∈ [ 0 , 10 ) x \in[0,10), \quad y \in[0,10) x∈[0,10),y∈[0,10)
1.1 解决步骤
- 利用现成函数绘制图形并求解出在给定区间的最大值
- 选用群智能算法(遗传算法, 粒子群算法, 蚁群算法), 初步设定参数, 分析结果
- 改变参数分析算法的性能
- 总结
1.2 问题粗析
利用Matlab绘制函数图形,及使用函数计算最大值如下, 可得函数在该区间的最大值在99.99附近.
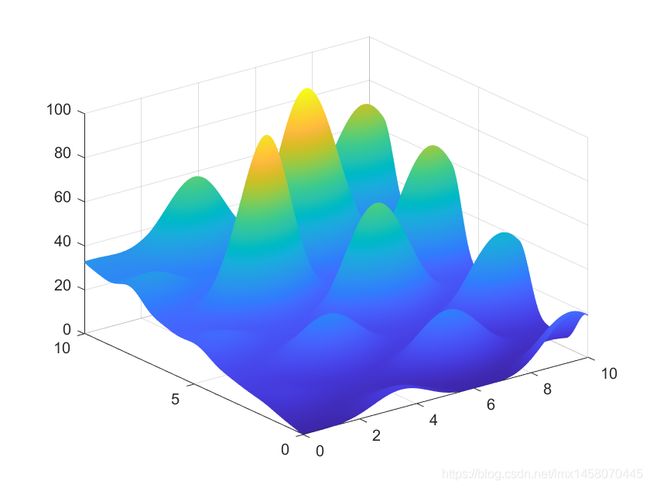
代码如下:
% 代码1 粗略绘制函数图形并求最值
clc
clear
clf
x = linspace(0,10,1000);
y = linspace(0,10,1000);
[X,Y] = meshgrid(x,y);
Z = 6.452*(X+0.125.*Y).*((cos(X)-cos(2.*Y)).^2)./sqrt(0.8+(X-4.2).^2+2.*(Y-7).^2)+3.226.*Y;
mesh(X,Y,Z)
hold on
2. 遗传算法求解
2.1 步骤
- 实数编码
- 群体设定
- 适应度函数
- 选择(复制)
- 交叉
- 变异
2.2 结果
利用Matlab的GA函数, 首先用默认参数进行试验, 发现易陷入局部最优解(如下图)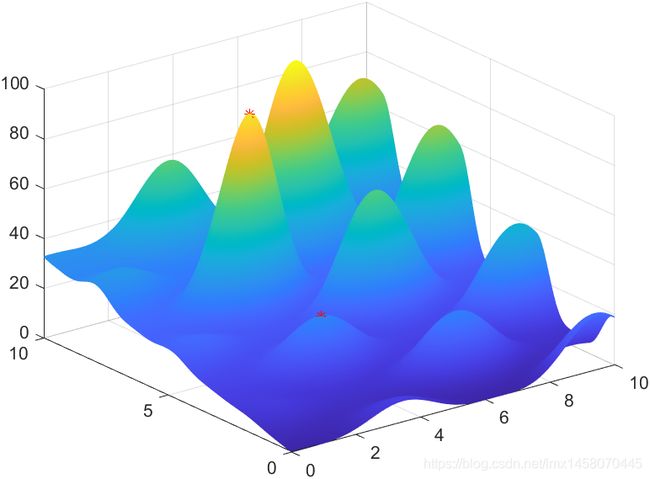
代码如下:
% 代码2 遗传算法
fun = @(x) 1/(6.452*(x(1)+0.125.*x(2)).*((cos(x(1))-cos(2.*x(2))).^2)./sqrt(0.8+(x(1)-4.2).^2+2.*(x(2)-7).^2)+3.226.*x(2));
nvars = 2;
A = [1, 0; 0, 1; -1, 0; 0, -1]; % Ax不大于b
b = [10; 10; 0; 0];
lb = [];
ub = [];
nonlcon = [];
IntCon = [];
options = optimoptions(@ga)
[x,fval,exitFlag,output,population,scores] = ga(fun,nvars,A,b,[],[],lb,ub,nonlcon,IntCon,options)
通过optimoptions函数对GA算法的options参数进行修改, 测试结果发现, 在种群规模不太小(>20), 将交配概率与变异概率分别设置为0.8和0.2, 容易找到最优解.
此时, 最优解的坐标为(6.0914, 7.7991, 99.9953).

代码如下:
fun = @(x) 1/(6.452*(x(1)+0.125.*x(2)).*((cos(x(1))-cos(2.*x(2))).^2)./sqrt(0.8+(x(1)-4.2).^2+2.*(x(2)-7).^2)+3.226.*x(2));
nvars = 2;
A = [1, 0; 0, 1; -1, 0; 0, -1]; % Ax不大于b
b = [10; 10; 0; 0];
lb = [];
ub = [];
nonlcon = [];
IntCon = [];
options = optimoptions(@ga, ...
'PopulationType', 'doubleVector',...
'PopulationSize', 50,... % 种群规模
'EliteCount', 1,... % 最佳个体保存
'CrossoverFraction', 0.8, ... % 交配概率
'MigrationDirection', 'forward',...
'MigrationInterval', 20,...
'MigrationFraction', 0.2,... % 变异概率
'Generations', 100,... % 迭代次数
'TimeLimit', Inf,...
'FitnessLimit', -Inf,...
'StallTest', 'averageChange',...
'StallTimeLimit', Inf,...
'TolFun',1.0e-06,...
'Tolcon',1.0e-03,...
'NonlinConAlgorithm','auglag',...
'InitialPenalty', 10,...
'PenaltyFactor', 100,...
'PlotInterval', 1,...
'MutationFcn', {@mutationadaptfeasible [1] [1]},... % 修改
'CreationFcn', @gacreationlinearfeasible,... % 修改
'FitnessScalingFcn', @fitscalingrank,...
'SelectionFcn', @selectionstochunif,...
'CrossoverFcn', @crossoverintermediate,... % 修改
'Display', 'final',...
'Vectorized', 'off')
[x,fval,exitFlag,output,population,scores] = ga(fun,nvars,A,b,[],[],lb,ub,nonlcon,IntCon,options)
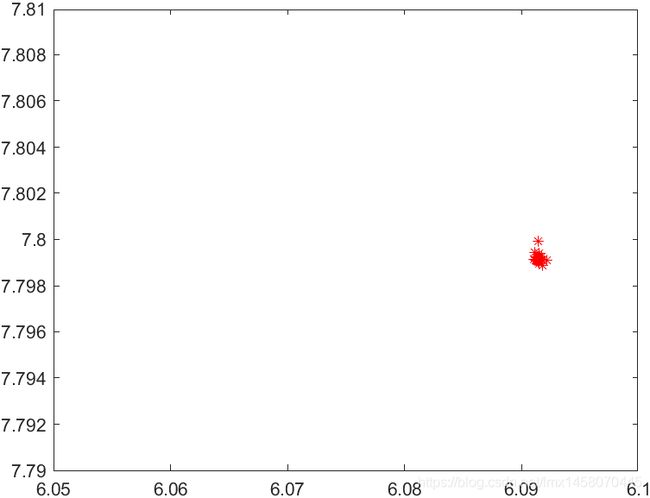
2.3 结果分析
clc
clf
figure(2)
plot(population(:,1),population(:,2),'*r')
xlim([6.05 6.10])
ylim([7.79 7.81])
2.4 遗传算法小结
- 在代码调试的过程中, 先是用默认参数进行试验, 发现如不设置参数, 能得出正确结果, 但是在使用optimoptions函数获取options参数后, 再赋值成一模一样的参数, 则得不到理想结果, 容易陷入局部最优解.
问题解决: 通过手动赋值所有参数, 采取控制变量法,每次修改其中一个参数, 最终对 ′ M u t a t i o n F c n ′ , ′ C r e a t i o n F c n ′ , ′ C r o s s o v e r F c n ′ 'MutationFcn', 'CreationFcn', 'CrossoverFcn' ′MutationFcn′,′CreationFcn′,′CrossoverFcn′三个参数进行默认值的修改(依据警告以及 d o c u m e n t a t i o n documentation documentation), 最终确定当
′ M u t a t i o n F c n ′ = @ m u t a t i o n a d a p t f e a s i b l e [ 1 ] [ 1 ] 'MutationFcn'={@mutationadaptfeasible [1] [1]} ′MutationFcn′=@mutationadaptfeasible[1][1],
′ C r e a t i o n F c n ′ = @ g a c r e a t i o n l i n e a r f e a s i b l e 'CreationFcn'=@gacreationlinearfeasible ′CreationFcn′=@gacreationlinearfeasible,
′ C r o s s o v e r F c n ′ = @ c r o s s o v e r i n t e r m e d i a t e 'CrossoverFcn'=@crossoverintermediate ′CrossoverFcn′=@crossoverintermediate
时, 算法得到正确结果. - 解决问题1后, 对种群规模, 交配概率, 变异概率等参数进行修改, 结果显示, 在在种群规模不太小(>20), 将交配概率与变异概率分别设置为0.8和0.2, 容易找到最优解.
- 在使用遗传算法对二元函数进行最值求解时, 没有选用根据步骤逐行书写代码, 而是使用Matlab自带的GA函数, 通过optimoptions对参数进行准确配置, 进而得到结果.
- 逐行书写代码有利于加深算法的数学理解, 原理的实现. 但在工程性方面, 自行书写代码性能不如算法工程师所写的GA函数, 因此, 在充分理解原理的基础上, 直接调用函数(或使用APP), 不仅有利于之后的再次使用, 而且对于各种参数的配置有了一定经验, 对于使用遗传算法解决其他类型问题有一定帮助.
3. 粒子群算法求解
3.1 步骤
- 下载工具箱, 并在Matlab中设置工具箱的路径;
- 定义待优化函数 t e s t f u n c test_func testfunc;
- 调用PSO算法的核心函数: p s o _ T r e l e a _ v e c t o r i z e d ( ) pso\_Trelea\_vectorized() pso_Trelea_vectorized().
3.2 结果
通过下载安装 P S O t PSOt PSOt工具箱, 对 t e s t _ f u n c . m test\_func.m test_func.m与 t e s t _ m a i n . m test\_main.m test_main.m文件进行编写, 设置初始参数后, 结果如下图所示.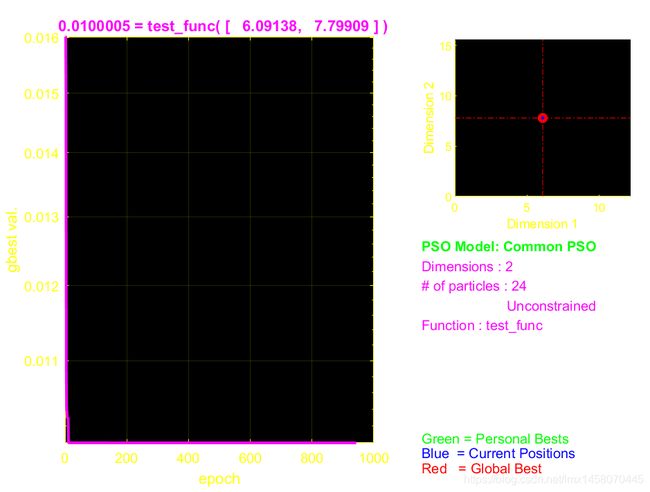
由图可知, 在迭代了大约700次后, PSO算法得出最大值点坐标(6.0914, 7.7991, 99.9953), 与遗传算法获得结果一致.
代码如下:
% test_func函数
function z=test_func(in)
nn=size(in);
x=in(:,1);
y=in(:,2);
nx=nn(1);
for i=1:nx
temp = 1/(6.452*(x(i)+0.125.*y(i)).*((cos(x(i))-cos(2.*y(i))).^2)./sqrt(0.8+(x(i)-4.2).^2+2.*(y(i)-7).^2)+3.226.*y(i));
z(i,:) = temp;
end
% test_main.m文件
clear
clc
x_range=[0,10]; %参数x变化范围
y_range=[0,10]; %参数y变化范围
range = [x_range;y_range]; %参数变化范围(组成矩阵)
Max_V = 0.2*(range(:,2)-range(:,1)); %最大速度取变化范围的10%~20%
n=2; %待优化函数的维数,此例子中仅x、y两个自变量,故为2
pso_Trelea_vectorized('test_func',n,Max_V,range) %调用PSO核心模块
3.3 结果分析
PSO算法中, 调用 p s o _ T r e l e a _ v e c t o r i z e d ( ) pso\_Trelea\_vectorized() pso_Trelea_vectorized()函数的 P S O p a r a m s PSOparams PSOparams参数含义如下表所示(自己查资料总结):
| 参数 | 含义 |
|---|---|
| P(1) | 命令窗显示的间隔数, 默认为100, 0则不显示中间过程 |
| P(2) | 最大迭代次数, 如算法不收敛, 自动停止, 默认为2000 |
| P(3) | 初始粒子数, 越多则越有可能收敛到全局最优值, 默认为24 |
| P(4) | 加速度参数, 影响局部最优值, 默认为2 |
| P(5) | 加速度参数, 影响全局最优值, 默认为2 |
| P(6) | 初始时刻加权值, 默认0.9 |
| P(7) | 收敛时刻加权值, 默认0.4 |
| P(8) | 当迭代次数超过此值时, 加权取其最小, 默认为1500 |
| P(9) | 终止算法的阈值, 连续两次迭代中对于的种群最优值小于此阈值时,算法停止, 默认为1e-25 |
| P(10) | 终止算法的阈值, 连续n次迭代函数的梯度没有变化,则算法停止 |
| P(11) | 说明优化的情况, NaN表示非约束下的优化问题 |
| P(12) | 0则表示通常的PSO算法 |
| P(13) | 0表示随机产生种子, 1表示用户自行产生种子 |
3.4 小结
- 在调用 p s o _ T r e l e a _ v e c t o r i z e d ( ) pso\_Trelea\_vectorized() pso_Trelea_vectorized()函数过程中, 出现 f o r c e r o w forcerow forcerow函数无法识别的问题, 通过查看PSOt文件夹, 发现在子文件夹路径下存在 f o r c e r o w . m forcerow.m forcerow.m文件, 将PSOt及其子文件夹全部添加到搜索路径后, 问题解决.
- 在使用粒子群算法对二元函数进行最值求解时, 通过网络下载PSOt工具箱, 编写 t e s t _ f u n c . m 函 数 test\_func.m函数 test_func.m函数,设置参数 x , y x,y x,y的变化范围,最大速度的取值,待优化函数的维数等参数, 进行调用, 得到结果.逐行书写代码有利于加深算法的数学理解, 原理的实现. 但在工程性方面, 自行书写代码性能不如算法工程师所写的 P s o _ P r e l e a _ v e c t o r i z e d Pso\_Prelea\_vectorized Pso_Prelea_vectorized函数, 因此, 在充分理解原理的基础上, 直接调用函数(或使用APP), 不仅有利于之后的再次使用, 而且对于各种参数的配置有了一定经验, 对于使用粒子群算法解决其他类型问题有一定帮助.
- 粒子群算法适合解决二元函数最优值问题, 仅需要调整少数几个参数即可实现函数的优化.