可泛化的表征学习

部分内容参考：寻找领域不变量：从生成模型到因果表征

在迁移学习和域自适应中，我们常常需要寻找领域不变的表征（Domain-invariant Representation），这种表示可被认为是学习到各领域之间的共性，并基于此共性进行迁移。而获取这个表征的过程就与深度学习中的“表征学习”联系紧密。生成模型，对比学习和最近流行的因果表征学习都可以视为获取良好的领域不变表征的工具。

生成模型

生成模型的视角是在模型中引入隐变量（Latent Variable），而学到的隐变量为数据提供了一个隐含表示（Latent Representation）。生成模型描述了隐变量$z$生成观测数据$x$的过程：

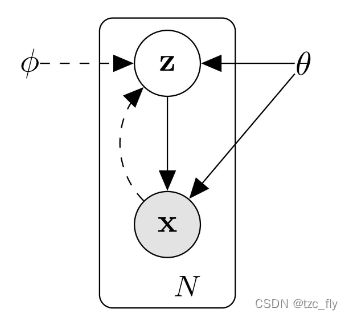
用概率可以表示为：$$p_{\theta }(x)=\sum _z{p}_{\theta }(x,z)=\sum _z{p}_{\theta }(z)p_{\theta }(x|z)$$其中，$p_{\theta }(x)$表示在生成器模型参数为$\theta$时，$x$出现的概率，$p_{\theta }(x,z)$则是$z$和$x$联合出现的概率，$p_{\theta }(x|z)$代表输入数据为$z$，生成$x$的概率。积分（求和）项${\sum }_z{p}_{\theta }(z)p_{\theta }(x|z)$很难计算。

变分自编码器

VAE的思想是采用变分近似后验分布$q_{\varphi }(z|x)$（对应编码器），数据的生成过程$p_{\theta }(x|z)$视为解码器。如下图所示：

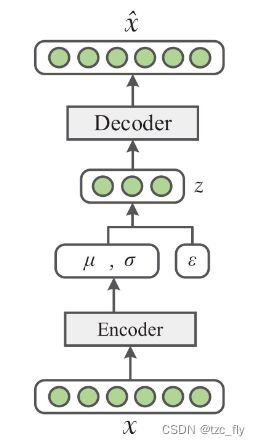
变分自编码器的优化目标为最大化与$x$关联的变分下界：$$max{L}_{VAE}(x;\theta ,\varphi )=-KL(q_{\varphi }(z|x)||p_{\theta }(z))+E_{z\sim q_{\varphi }(z|x)}(log{p}_{\theta }(x|z))$$第一项使近似的$z$后验分布$q(z|x)$和先验分布$p_{\theta }(z)$（人为设为高斯分布）尽可能接近（这样的目的是使解码器的输入尽可能服从高斯分布，从而使解码器对随机输入也有很好的输出），第二项为解码器的对数似然。

接下来是如何从近似后验分布$q(z|x)$采样$z$，因为$z$不是由一个函数产生，而是由一个随机采样过程产生（它的输出会随我们每次查询而发生变化），故直接用一个神经网络$z=g(x)$表示是不合理的，需要一个重参数化技巧：$$z=g_{\varphi }(ϵ,x)=\mu +\sigma \odot ϵ$$$$\mu ,\sigma =Encode{r}_{\varphi }(x)$$$$ϵ\sim N(\text{0},\text{I})$$这样就能使得$z$来自随机采样，并通过反向传播训练。

条件变分自编码器

这是在VAE基础上增加了条件信息$c$（数据$x$的标签信息）：

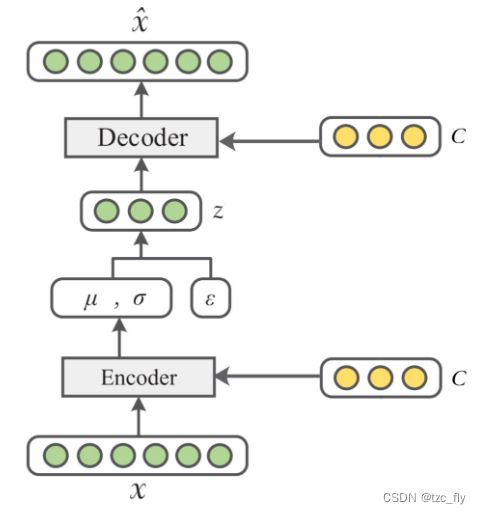
因此，优化目标表示为：$$max{L}_{CVAE}(x,c;\theta ,\varphi )=-KL(q_{\varphi }(z|x,c)||p_{\theta }(z|c))+E_{z\sim q_{\varphi }(z|x,c)}(log{p}_{\theta }(x|z,c))$$对于在MNIST训练完的VAE和CVAE，可以可视化隐向量$z\sim q_{\varphi }(z|x)$和$z\sim q_{\varphi }(z|x,c)$：

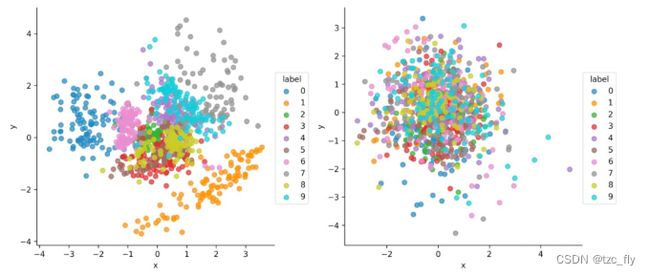
可以看到CVAE的隐空间相比VAE的隐空间没有编码标签信息，而是编码其他关于数据$x$的分布信息，这可以视为一种解耦的表征学习（disentangled representation learning）：将不同标签的分布解耦开，比如0到9的10个分布都归一化到标准正态分布。

就领域自适应任务而言，训练生成模型获得了隐向量之后就已经完成目标，之后可以将隐向量拿到其它领域的任务中去用了。不过有时训练生成模型的最终目的还是为了生成原始数据。接下来对比两者的图像生成效果。

关于VAE的重点理解

注意观察重参数的式子：$$z=g_{\varphi }(ϵ,x)=\mu +\sigma \odot ϵ$$我们首先要明白，$z$并不是服从标准正态分布的，它服从$N(\mu ,\sigma )$。在引入$KL(q_{\varphi }(z|x)||p_{\theta }(z))$之前，VAE的学习目标仅有对数似然，换言之，此时关于编码器是未知的，为了规范化（正则化）编码器，VAE强行将所有$z$的分布$q_{\varphi }(z|x)$对齐到一个固定的分布即$p_{\theta }(z)$。这样做的好处在于，将距离较远的簇的分布拉近，最终可以表现为所有$z$的分布都比较集中，这可以确保整体分布的连续性。

因此，对于VAE的隐变量，不仅在整体上呈现标准正态分布，具体的局部簇也符合某个高斯分布（具体的局部簇对应一个category）。

扩展内容：特征提取+对抗训练

本节内容来自：Federated Learning with Domain Generalization

首先提及联邦学习Federated Learning，联邦学习分为四个步骤：

• 所有客户端分别独立地在本地数据上进行训练；
• 客户端对模型参数或者模型参数的梯度进行加密，上传到服务器；
• 服务器对搜集到的客户端的模型参数或者梯度进行聚合，并且是安全聚合（Secure Aggregation）；
• 服务器将模型下发到各个客户端；

FL使一组客户端能够在集中服务器的帮助下联合训练机器学习模型。客户端在训练期间不需要向服务器提交本地数据，因此客户端的本地训练数据受到保护。在FL中，分布式客户端独立收集其本地数据，因此每个客户端的数据集可能自然形成不同的源域。实际上，在多个源域上训练的模型在不可见的目标域上可能具有较差的泛化性能。

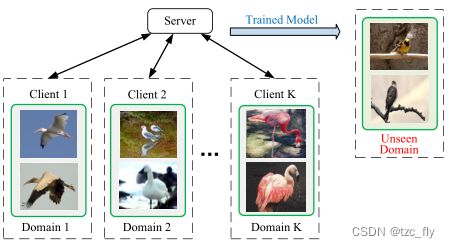
在FL中，$K$个不同的客户端协同训练一个机器学习模型来完成对象分类任务。每个客户端的数据形成一个不同的源域。该工作的目标是开发一个解决方案来学习一个分类器（在多个源域上），该分类器可以在Unseen domain上也能表现良好。

提取领域不变的表示也可以通过简单的 “特征提取器 + GAN 对抗训练” 来得到。如下图Client1设置了一个生成器根据随机噪声和标签编码（one-hot向量形式）来生成 “伪” 特征，并训练判别器来区分特征提取器得到的特征和"伪" 特征。此外，还采用了随机投影层来使得判别器更难区分这两种特征，使得对抗网络更稳定。

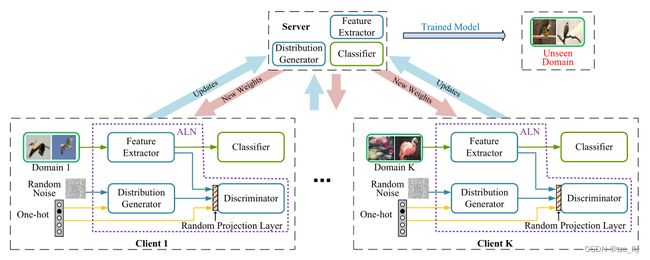
• 直观理解，上图的精髓在于：每个Client都将各自的source domain对齐到reference分布上，而reference分布是人为设置的先验分布（one-hot+随机噪声），因此使得source domain的特征投影到同一个空间下，从而可以学习到用于域泛化的领域不变表示（domain-invariant representation）。

---

总结上面3个生成模型，我们可以发现其之所以可以学习域不变表征，是因为我们将隐变量的后验分布人为对齐到固定的先验分布，限制了特征的表征空间。

---

对比学习

在自监督预训练中，我们要求该过程能够学习出一些对建模$p(y|x)$（对应于下游分类任务）同样有用的特征。因为如果$y$与$x$的成因相关，则$p(x)$应当和$p(y|x)$存在联系，故试图找到变化潜在因素的自监督表示学习会非常有用。自然语言处理中的经典模型 BERT 便是基于自监督学习的思想。

对比学习属于自监督，通过构造anchor样本，正样本，负样本之间的关系来学习表征。对于任意anchor样本$x$，我们用$x^{+}$和$x^{-}$分别表示正样本和负样本，$f(\cdot )$表示要训练的特征提取器。此时，学习目标为限制anchor与负样本的距离远大于与正样本的距离（此处的距离为在表征空间的距离）：$$d(f(x),f(x^{+}))\ge d(f(x),f(x^{-}))$$其中，$d(\cdot ,\cdot )$为距离的度量，常用的是余弦相似度：$$cos(a,b)=\frac{a\cdot b}{||a||\times ||b||}$$当$a,b$归一化后，余弦相似度等价于向量内积。

此外，互信息也可以作为相似度的度量。在经典的 SimCLR 架构按照如下图所示的图像增强（比如旋转裁剪等）方式产生正样本：

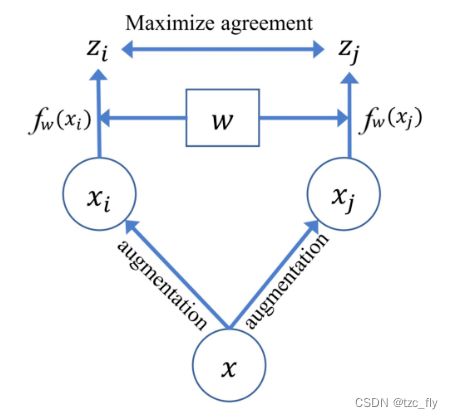
如上图所示，它对每张输入的图片进行两次随机数据增强（如旋转剪裁等）来得到$x_i,x_j$。对于$x_i$来说，$x_j$为其正样本，数据集剩下$N-1$个样本为负样本。

对比学习一般也是用来获取 embeddings，然后用于下游的有监督任务中。

---

依靠正样本和负样本的对比刺激，对比学习可以运用数据增强来捕捉正确的域不变特征。在泛化视角，这相比 “单纯的数据增强+直接监督学习正样本” 显得更加明确。

但我个人认为，对比学习可以学习泛化表征的另一个原因在于，对比学习侧重于学习样本之间的信息，这样做可以将样本均匀地在超球面空间上拉开距离，但是注意，前提是需要包含足够数据，模型才能学会将样本投影到同一个全局的超球面空间，这或许是CLIP这种大模型在大数据支撑下表现出色的原因。

因此，对比学习的两个特点应该是：

• 从小范围样本pairs级别看，模型学习到域不变特征；
• 从大范围的数据集规模看，模型将样本均匀映射到超球面，避免了不同类别分布的过度集中。

---

因果推断视角

本节内容来自：Causality Inspired Representation Learning for Domain Generalization

前面提到在对比学习中可以运用数据增强来捕捉域不变特征，然而这种数据增强的框架也可以从因果表征学习的视角来看。因果推断中的因果不变量同样也可以对应到领域不变的表征。

原始数据$X$由因果因子$S$（图像本身的语义）和非因果因子$U$（图像的风格）混合决定，且只有$S$能够影响原始数据的类别标签。

我们不能将原始数据量化为$X=f(S,U)$，因为因果和非因果因子一般不能观测到并且不能被形式化。

我们的任务应该是将因果因子$S$从原始数据提取出来，而这可以在因果干预$P(Y|do(U),S)$的帮助下完成。下面将对CIRL进行具体描述。

CIRL提出背景

为了提高泛化能力，人们提出了很多DG方法（Domain generalization），但目前存在一个固有问题，这些努力只是试图弥补OOD数据造成的问题，并对数据和标签之间的统计相关性建模，而没有解释潜在的因果机制。例如，在图像分类任务中，很可能所有长颈鹿都在草地上，表现出高度的统计依赖性，当目标域中的背景变化时，这很容易误导模型做出错误的预测。毕竟，长颈鹿的头部、颈部等特征才构成了长颈鹿。

CIRL引入结构因果模型（SCM）来形式化DG问题，旨在挖掘数据和标签之间的内在因果机制，并获得更好的泛化能力。具体来说，假设category-related信息作为因果因子（causal factors），因果因子与label的关系独立于domain。比如数字识别中的"shape"。而独立于category的信息被认为是非因果因子（non-causal factors），这通常是与domain相关的信息，例如数字识别中的"handwriting style"（笔迹风格）。每个原始数据$X$由因果因子$S$和非因果因子$U$混合而成，只有前者对类别标签$Y$产生因果影响，如下图所示。

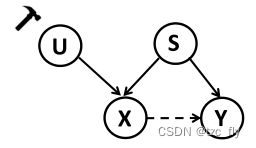
• DG的SCM，实线箭头表示父节点导致子节点；而虚线箭头表示存在统计相关性。$X$是原始数据，$Y$是标签。

我们的目标是从原始输入$X$中提取因果因子$S$，然后重建不变的因果机制，其可以基于因果干预$P(Y|do(U),S)$完成。$do(\cdot )$表示对变量的干预。

CIRL认为，因果因子$S$应满足三个属性：

• 从非因果因素$U$中分离出来；
• $S$的因式分解应该是联合独立的；
• 足以完成分类任务$X\to Y$是指包含所有因果信息。

如下图a所示，与$U$的混合使$S$包含潜在的（underlying）非因果信息，而联合依赖因子分解（dependent factorization）时会使$S$冗余，进一步导致遗漏一些潜在的因果信息。相反，图b中的因果因子$S$是满足所有要求的理想因子。受此启发，提出了一种因果激励表示学习（CIRL，Causality Inspired Representation Learning）算法，强制所学习的表示具有图b的性质，然后利用表示的每个维度模拟因果因子的因式分解，从而具有更强的泛化能力。

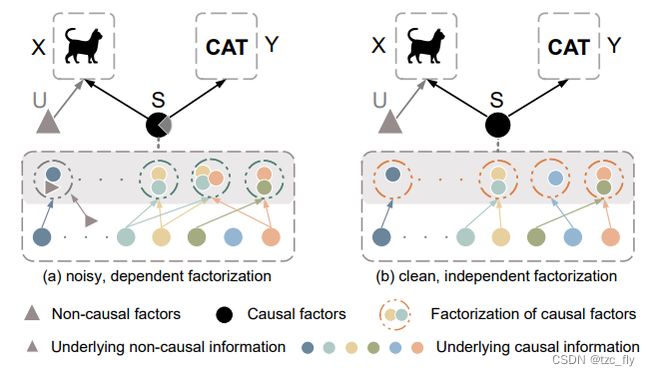
• 因果因子的三个特性的说明。

简而言之，对于每个输入，我们首先利用因果干预模块（causal intervention module），通过生成带有扰动领域相关信息的新数据，将因果因子$S$与非因果因子$U$分开。与原始数据相比，生成的数据具有不同的非因果因子$U$，但具有相同的因果因子$S$，因此表征被强制保持不变。此外，利用因子分解模块（factorization module），使表征的每个维度联合独立，然后可以用来近似因果因子。此外，为了便于分类，使用对抗掩码模块，该模块反复检测包含相对较少因果信息的维度，并通过掩码器和表征生成器之间的对抗学习，迫使它们包含更多新颖的因果信息。

基础：补充内容

在开始了解具体方法前，我们需要了解两个原则：

• 原则1-Common Cause Principle（共同原因原则）：如果两个观测值$X$和$Y$在统计上是相关的，那么就存在一个变量$S$，它会对两者产生因果影响，并解释所有依赖性，即当条件为$S$时，$X$和$Y$是独立的；
• 原则2-Independent Causal Mechanisms（独立因果机制）：每个变量的条件分布及其原因（即其机制）不会影响其他机制。

对于原则1，我们将SCM形式化以描述DG问题：$$X:=f(S,U,V_1),S\perp U\perp V_1$$$$Y:=h(S,V_2)=h(g(X),V_2),V_1\perp V_2$$其中，$X,Y$代表输入图像和对应的label，$S$代表影响$X$和$Y$的因果因子，比如与类别相关的信息，如数字识别中的"shape"，而$U$表示仅影响$X$的非因果因子，通常是与领域相关的信息比如"style"。$V_1$、$V_2$是共同独立的无法解释的噪声变量（$\perp$代表相互独立）。对于$f$、$h$、$g$，它们可以看作是未知的结构函数。因此，对于任何分布$P(X,Y)$，如果因果因子$S$给定，就存在一个条件分布$P(Y|S)$，比如：不变的因果机制（invariant causal mechanism）。基于上述讨论，如果我们能够获得因果因子，那么通过优化$h$：$$h^{\ast }=\arg \underset{h}{\min }{E}_P[l(h(g(X)),Y)]=\arg \underset{h}{\min }{E}_P[l(h(S),Y)]$$其中，$l(\cdot ,\cdot )$代表交叉熵损失。

不幸的是，因果因子$S$并不是事先提供给我们的，我们得到的是原始图像$X$，而这些图像通常是非结构化的。直接重建因果因子和机制是不切实际的，因为它们是不可观测和不明确的。然而，显而易见的是，因果因子仍然需要遵守某些要求。以前的工作声明，因果因子应该是共同独立的，如原则2所示。

因为$S$代表所有因果因子的集合$\left\{s_1,s_2,...,s_N\right\}$，原则2告诉我们：

• 改变或干预一种机制$P(s_i|P{A}_i)$不会改变其他任何机制$P(s_j|P{A}_j)$，$i\ne j$，$P{A}_i$代表causal graph中$s_i$的父节点，可以将其视为$s_i$包含的因果信息。
• 了解机制$P(s_i|P{A}_i)$并不能得到机制$P(s_j|P{A}_j)$的信息。

因此，我们可以将因果因子的联合分布分解为下列条件分布：$$P(s_1,s_2,...,s_N)=\prod _{i=1}^{N}P(s_i|P{A}_i)$$因此，我们强调，基于共同原因原则（原则1）中因果变量的定义和ICM原则（原则2）中因果机制的性质，因果因子$S$应满足三个基本属性：

• 因果因子$S$应该与非因果因子$U$分开，即$S\perp U$，因此，对$U$进行干预不会影响$S$；
• 因子分解$s_1,s_2,...,s_N$应该是联合独立的；
• 因果因子$S$应足以满足分类任务$X\to Y$的因果关系，即包含可以解释$X,Y$之间所有统计相关性的信息。

基于这3个属性，我们建议通过强迫网络的表示具有与因果因子相同的属性来学习因果表征，而不是直接理想化地重构因果因子。

CIRL方法

CIRL由3个模块组成：causal intervention module（因果干预模块），causal factorization module（因果因子分解模块）和adversarial mask module（对抗掩码模块），CIRL框架如下图：

• CIRL对非因果因子采用因果干预来生成增强后的图像，然后将原始和增强图像的表征送到因子分解模块，该模块使用分解损失函数来迫使图像表征和非因果因子分离。最后，通过对抗掩码模块让生成器和掩码器之间形成对抗，使得表征更适用于之后的分类任务。

因果干预模块

我们首先旨在通过因果干预将因果因子$S$从非因果因子$U$的混合中分离出来。我们已经知道因果因子$S$应该对$U$的干预保持不变，即$P(S|do(U))$不变。在DG的相关工作中，我们确实知道一些领域相关信息无法确定输入的类别，可以将其视为非因果因素，并通过一些技术捕获。例如，傅里叶变换有一个众所周知的特性：傅里叶谱的相位分量保留了原始信号的高级语义，而振幅分量包含低级统计信息。因此，我们通过干扰振幅信息而对$U$进行干预，同时保持相位信息不变。形式上，给定原始输入图像$x^o$，其傅里叶变换可以表示为：$$\mathcal{F}(x^o)=A(x^o)\times e^{-j\times P(x^o)}$$其中，$A(x^o),P(x^o)$分别表示振幅（amplitude）和相位（phase）分量。傅里叶变换$\mathcal{F}(\cdot )$和其逆变换${\mathcal{F}}^{-1}(\cdot )$可以用FFT进行有效计算。然后，我们通过在原始图像$x^o$的振幅谱和从任意源域随机采样的图像$(x^{\prime }{)}^o$之间进行线性插值扰动振幅信息：$$A(x^o)=(1-\lambda )A(x^o)+\lambda A((x^{\prime }{)}^o)$$其中，$\lambda \sim U(0,\eta )$，$\eta$控制扰动强度。然后，我们将扰动振幅谱与原始相位分量结合，用傅里叶逆变换生成增强后的图像$x^a$：$$\mathcal{F}(x^a)=A(x^o)\times e^{-j\times P(x^o)},x^a={\mathcal{F}}^{-1}(\mathcal{F}(x^a))$$将CNN模型实现的表示生成器记为$g(\cdot )$，表示记为$r=g(x)\in R^{1\times N}$，其中$N$是维数，为了模拟对$U$的干预保持不变的因果因子，优化$g$：$$\underset{g}{\max }\frac{1}{N}\sum _{i=1}^{N}COR({\tilde{r}}_i^o,{\tilde{r}}_i^a)$$其中，${\tilde{r}}_i^o,{\tilde{r}}_i^a$分别代表$R^o=[(r_1^o{)}^T,...,(r_B^o{)}^T{]}^T\in R^{B\times N}$和$R^a=[(r_1^a{)}^T,...,(r_B^a{)}^T{]}^T\in R^{B\times N}$的第$i$列Z-score标准化。$B$代表batch-size。

$r_j^o=g(x_j^o)$和$r_j^a=g(x_j^a)$，$j\in \left\{1,...,B\right\}$。我们利用COR函数（计算相关性）来衡量干预前后表征的相关性。因此，我们可以通过使其独立于$U$来实现用表征$R$模拟因果因子$S$的第一步。

因果因子分解模块

如原则2，因果因子$s_1,...,s_N$的因子分解应该是联合独立的，不需要其他因子的信息，因此，我们应该使表征的任何两个维度相互独立：$$\underset{g}{\min }\frac{1}{N(N-1)}\sum _{i\ne j}COR({\tilde{r}}_i^o,{\tilde{r}}_i^a)$$为了节省计算成本，我们统一$g$的两个优化目标，建立相关性矩阵$C$（correlation matrix）：$$C_{ij}=\frac{<{\tilde{r}}_i^o,{\tilde{r}}_i^a>}{||{\tilde{r}}_i^o||\cdot ||{\tilde{r}}_i^a||},i,j\in 1,2,...,N$$其中，$<\cdot ,\cdot >$表示内积操作。因此，因此，$R^o$和$R^a$的同一维度可以被视为需要最大化相关性的正对（positive pairs），而不同维度可以被看作需要最小化相关性的负对（negative pairs）。基于此，得到了因子分解损失$L_{Fac}$：$$\underset{g}{\min }{L}_{Fac}=\frac{1}{2}||C-I|{|}_F^2$$优化上面的目标可以使相关矩阵$C$的对角元素近似于1，这意味着非因果因子干预前后的表示是不变的。这表明我们可以有效地将因果因子从非因果因子的混合中分离出来。此外，它还使$C$的非对角线元素接近0，即强制让表征的维度联合独立。因此，通过最小化$L_{Fac}$，我们可以使表征满足理想因果因子的前两个特性。

对抗掩码模块

为了成功完成分类任务$X\to Y$，表征应该是因果充分的，即包含所有支撑信息。最直接的方法是在多个源域中使用监督标签$y$：$$L_{cls}=l(h(g(x^o)),y)+l(h(g(x^a)),y)$$其中，$h$是分类器。然而，这种直截了当的方法不能保证我们所学表征的每个维度都是重要的（不能包含足够的潜在因果信息用于分类）。具体来说，可能存在携带相对较少因果信息的劣质维度（inferior dimensions），对分类做出较小贡献。因此，我们应该检测这些维度并强制它们做出更多贡献。由于在因子分解模块的帮助下，维度也需要联合独立，因此，检测到的inferior dimensions被渲染为包含更多新的因果信息，而其他维度没有包含这些信息，这使得整个表示更具因果性。

因此，为了检测inferior dimensions，我们设计一个对抗性掩码模块。我们构建了一个基于神经网络的掩码，用$w$表示，以学习每个维度的贡献（输出向量$m\in R^N$），这些维度对应于较大的比率$\kappa \in (0,1)$被视为superior dimensions（优质维度），其余被视为inferior dimensions。

我们将表征乘以获得的掩码$m$和$1-m$，可以分别突出表征的superior dimensions和inferior dimensions。然后，我们将它们输入两个不同的分类器$h_1,h_2$，$L_{cls}$被写成：$$L_{cls}^{sup}=l(h_1(r^o\odot m^o),y)+l(h_1(r^a\odot m^a),y)$$$$L_{cls}^{inf}=l(h_2(r^o\odot (1-m^o)),y)+l(h_2(r^a\odot (1-m^a)),y)$$从上面式子可以看到这是一个对抗的行为，CIRL的最终优化目标为：$$\underset{g,h_1,h_2}{\min }{L}_{cls}^{sup}+L_{cls}^{inf}+L_{Fac}$$$$\underset{w}{\min }{L}_{cls}^{sup}-L_{cls}^{inf}$$