网络流-最大流问题详解（C++实现）

一，算法背景与理论

1.1 前言

1，本文将深入探讨最大流问题的dinic算法求解。
2，本文代码通过C++实现，不涉及算法竞赛知识，代码实现着重于结构化以及功能而非性能。
3，本文关注点在最大流的实现，而其中遇到的其他算法不会深入讨论(深度优先搜索DFS，广度优先搜索BFS)

1.2 基本概念介绍

在最大流问题中，网络可以看成一个带权重的有向无环图。

• 源点(S)： 该有向图中的一个特殊的点，只出不进，被称作源点。
• 汇点(T)： 该有向图中另一个特殊的点，只进不出，被称作汇点。
• 容量(maxV)： 记录每条边最大可通过的流量。
• 流量(flow)： 记录当前边上通过的流量。
• 最大流(maxFlow)： 从源点出发，通过重重有向边容量的约束，最终能到达汇点的最大流量被称作最大流。

简单来说：就好比水厂送水，源点相当于水厂，汇点相当于你家，每个有向边相当于每条输水管道，而容量相当于每条输水管道的最大容纳量。于是最大流问题就可以理解成为计算同一时间你家最多能获得多少水。

1.3 算法步骤详解

以下图为例：

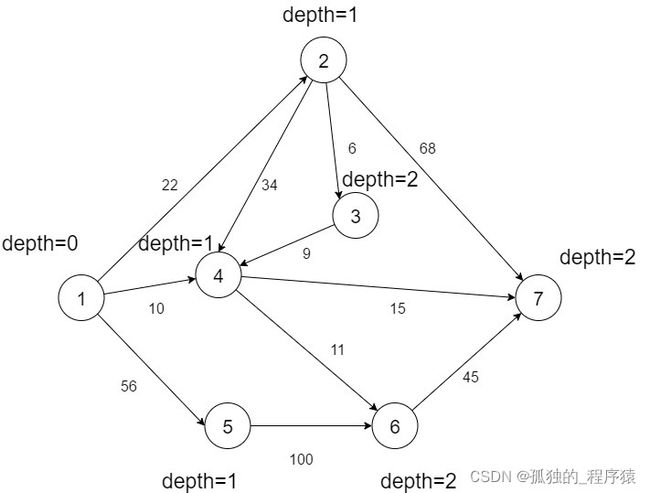
其中节点1为源点，节点7为汇点，通过观察上图，我们很容易得到该图最大流是：

1->2->7 flow:22
1->4->7 flow:10
1->5->6->7 flow:45
maxFlow = 77

那么如何通过计算机实现这一过程呢?

了解过算法的都应该知道图的遍历可以通过深度优先搜索的方式进行。于是我们就可以很容易的通过深度优先搜索从源点开始向汇点进行搜索，并且在搜索过程中不断更新边的权值。为此我们引入残量的概念。残量： 记录当前边所剩余的容量(即最大容量-当前流量)。

当一条边的残量为0，则这条边可以看作是一条断边。

那么如何知晓此时汇点达到了最大流？

可以利用BFS计算每一个节点的深度，我们引入增广路的概念。
增广路： 能使汇点流量增大的通路。

于是最大流问题也可以理解为找增广路的过程，当整个图中不在存在增广路的时候也就说明此时汇点流量达到了最大值。
利用BFS标记节点深度，当汇点深度无法被标记的时候，就说明整个图中再也没有能到达汇点的通路，也就是没有增广路。

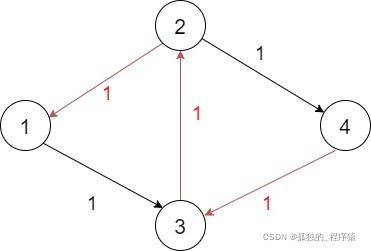
但有的时候总会遇到预料之外的情况，如下图：

通过图像，我们很清楚的知道若使汇点流量最大，最优通路应该是：

1->2->4 flow:1
1->3->4 flow:1
maxFlow=2

可是假如当出现以下情况时:

此时DFS为我们选择了1->2->3->4这条路，但显然不是最优的情况，可是因为是有向图，搜索无法回退。

如何使算法反悔？

可以通过加反边的方式实现算法反悔，为每两个连接的节点之间添加一条残量为0的反边。DFS经过时使原始边减去当前流量的同时为反边加上当前流量，从而实现反悔。简单来说就是当水不想从这个管道输送的时候，这个管道就将把水退回上一个节点。

所以整体算法思路就是BFS确定节点深度，DFS搜索更新残量并返回此次搜索为汇点增加的流量值，然后继续BFS确定新的节点深度，再DFS搜索更新残量并返回此次搜索为汇点增加的流量值，直到BFS发现无法到达源点时，算法停止。

1.4 算法示例

以下图为例，首先通过BFS确定每一个节点，并规定当前节点只能由depth-1的节点扩展得到，例如depth=2的节点，只能由depth=1的节点扩展得到。这样做首先是避免了大量不必要的搜索，其次是解决了加反边后产生的回路造成的死循环的影响。

经过一轮DFS后剩余的边如下图所示(这里省略了所有残量为0的边)：

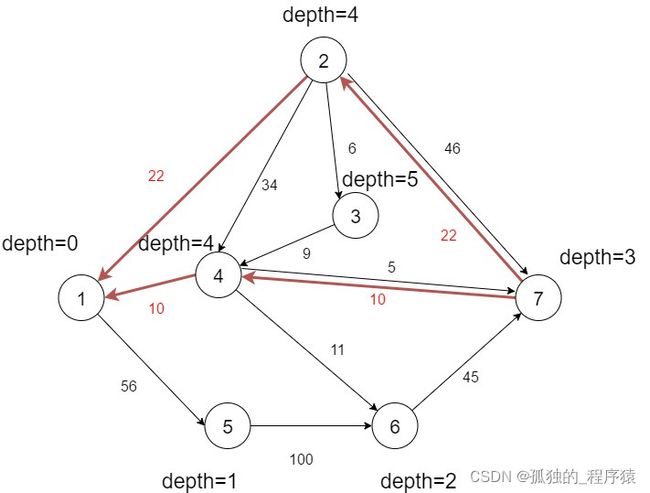
此时汇点流量为 32:

1->2->7 flow:22
1->4->7 flow:10

再利用BFS计算更新每个节点的深度，然后继续通过DFS进行搜索,得到1->5->6->7 flow:45，循环往复直到不存在增广路，最终得到最大流为77。

二，代码展示

代码无非是解决以下几个问题：
1,读取图信息，本文是通过读取txt文本文件来获取网络流信息，然后在NetworkFlow.h中确定汇点与源点。

// 创建网络图
    1 2 22
    1 4 10
    1 5 56
    2 3 6
    2 4 34
    2 7 68
    3 4 9
    4 6 11
    5 6 100
    4 7 15
    6 7 45

2，创建网络流图，本文利用结构体作为节点数据类型，结构体包含3个变量，分别是当前节点深度，当前节点存储的数据(这个感觉写的时候有点多此一举)，当前节点包含的边集，由一个键值对表示，分别代表指向的节点编号以及边的最大容量。然后利用map存储图所有的节点。

3，为所有节点加反边。

4，利用BFS计算节点深度。

5，利用DFS找到增广路，并更新残量。，在本文的dfs函数中出现了三个变量，flow，rest，delta。其中flow表示当前路线上所能承载的最大流量，rest是当前边的残量，delta是该条路上将要更新的流量值。

6，继续执行4，5两步直到汇点的深度为-1，即不存在增广路是停止。

2.1 NetworkFlow.h

    #pragma once
    #include 
    #include 
    #include 
    #include 
    #include 
    
    using namespace std;
    
    #define INF 0x3F3F3F	// 理论最大值
    #define T 7				// 汇点
    #define S 1				// 源点
    
    // 定义网络节点
    typedef struct node {
    	int data;
    	
    	// 存储边集，这里使用set数据结构感觉会更好，加反向边的时候会方便很多。
    	vector<pair<int, int>> edge;
    
    	int depth=-1;
    
    	node(int data, vector<pair<int, int>> edge) {
    		this->data = data;
    		this->edge = edge;
    	}
    }Node;
    
    // 初始化网路
    map<int, Node> initNetwork();
    
    // 格式化文件输入的数据
    vector<int> formatInput(string str);
    
    // 加反向边
    map<int, Node> addReverseEdge(map<int, Node> networkFlow);
    
    // 深度优先搜索计算节点深度
    bool bfs(map<int, Node> &networkFlow);
    
    // 深度优先搜索求增广路
    int dfs(int currentNode, int flow, map<int, Node> &networkFlow);
    
    // dinic算法求最大流
    int dinic(map<int, Node> networkFlow);
    
    // 重置深度
    void resetting(map<int, Node> &networkFlow);

2.2 NetworkFlow.cpp

    #include 
    #include 
    
    #include "NetworkFlow.h"
    
    
    using namespace std;
    
    // 初始化图结构
    map<int, Node> initNetwork() {
    
    	map<int, Node> networkFlow;
    	map<int, Node>::iterator iter;
    
    	ifstream network("./network.txt");
    	string str;
    
    	if (!network.is_open()) {
    		cout << "File can't open" << endl;
    		exit(0);
    	}
    
    	while (getline(network, str)){
    		vector<int> formatNodeInfo = formatInput(str);
    		
    		int prev = formatNodeInfo[0];
    		int next = formatNodeInfo[1];
    		int volume = formatNodeInfo[2];
    		
    		iter = networkFlow.find(prev);
    		if (iter == networkFlow.end()){
    			networkFlow.insert(pair<int, Node>(prev, Node(prev, {})));
    		}
    
    		iter = networkFlow.find(next);
    		if (iter == networkFlow.end()) {
    			networkFlow.insert(pair<int, Node>(next, Node(next, {})));
    		}
    
    		iter = networkFlow.find(prev);
    		iter->second.edge.push_back(pair<int, int>(next, volume));
    	}
    	return networkFlow;
    }
    
    // 格式化输入数据
    vector<int> formatInput(string str) {
    	vector<int> formatNodeInfo;
    	for (int i = 0; i < str.length(); i++) {
    		string temp = "";
    		while (str[i] != ' ' && i < str.length()) {
    			temp = temp + str[i];
    			i++;
    		}
    		formatNodeInfo.push_back(atoi(temp.c_str()));
    		temp.clear();
    	}
    	return formatNodeInfo;
    }
    
    // 加反向边
    map<int, Node> addReverseEdge(map<int, Node> networkFlow) {
    	map<int, Node> resultNetwork = networkFlow;
    	
    	map<int, Node>::iterator iter;
    
    	for (iter = networkFlow.begin(); iter != networkFlow.end(); iter++) {
    		for (auto item : iter->second.edge) {
    			int next = item.first;
    			int volume = item.second;
    
    			map<int, Node>::iterator iter_temp;
    
    			iter_temp = resultNetwork.find(next);
    			if (iter_temp != resultNetwork.end()) {
    				iter_temp->second.edge.push_back(pair<int, int>(iter->first, 0));
    			}
    			else {
    				cout << "添加反向边错误，未找到指向节点" << endl;
    			}
    
    		}
    	}
    	return resultNetwork;
    }
    
    // 广度优先搜索求节点深度
    bool bfs(map<int, Node> &networkFlow) {
    	resetting(networkFlow);
    	queue<int> q;
    	q.push(S);
    	networkFlow.find(S)->second.depth = 0;
    	map<int, Node>::iterator iter;
    	while (!q.empty()) {
    		int currentNode = q.front();
    		q.pop();
    		iter = networkFlow.find(currentNode);
    		if (iter == networkFlow.end()) {
    			cout << "bfs错误" << endl;
    			exit(0);
    		}
    		else {
    			for (auto i : iter->second.edge) {
    				int next = i.first;
    				int volume = i.second;
    				map<int, Node>::iterator iter_next = networkFlow.find(next);
    				if (volume != 0 && iter_next->second.depth == -1) {
    					iter_next->second.depth = iter->second.depth + 1;
    					q.push(i.first);
    				}
    			}
    		}
    	}
    	return networkFlow.find(T)->second.depth != -1;
    }
    
    // 深度优先搜索求增广路
    int dfs(int currentNode, int flow, map<int, Node> &networkFlow) {
    	if (currentNode == T) {
    		return flow;
    	}
    	int rest = flow;
    	map<int, Node>::iterator iter = networkFlow.find(currentNode);
    	map<int, Node>::iterator iter_next;
    
    	// 计算当前节点度数
    	int numOfEdge = iter->second.edge.size();
    	for (int i = 0; i < numOfEdge; i++) {
    		int nextNode = iter->second.edge[i].first;
    		int volume = iter->second.edge[i].second;
    
    		iter_next = networkFlow.find(nextNode);
    		if (iter->second.depth+1 == iter_next->second.depth && volume != 0 && rest != 0) {
    			int delta = dfs(iter_next->first, min(volume, rest), networkFlow);
    			if (!delta) {
    				iter_next->second.depth = 0;
    			}
    			// 更新边的容量，正边减，反边加
    			iter->second.edge[i].second -= delta;
    			vector<pair<int, int>>::iterator iter_ve;
    			for (iter_ve = iter_next->second.edge.begin(); iter_ve != iter_next->second.edge.end(); iter_ve++) {
    				if (iter_ve->first == currentNode) {
    					break;
    				}
    			}
    			iter_ve->second += delta;
    			rest -= delta;
    		}
    	}
    	return flow - rest;
    }
    
    // dinic算法求最大流
    int dinic(map<int, Node> networkFlow) {
    	int result = 0;
    	while (bfs(networkFlow)) {
    		result += dfs(S, INF, networkFlow);
    	}
    	return result;
    }
    
    // 重置深度
    void resetting(map<int, Node> &networkFlow) {
    	map<int, Node>::iterator iter;
    	for (iter = networkFlow.begin(); iter != networkFlow.end(); iter++) {
    		iter->second.depth = -1;
    	}
    }