数据结构—图/无向图/连通图/连通分量/邻接矩阵/表/广度深度遍历
1
在下图所示的各无向图中:

(1)找出所有的简单环。
(2)哪些图是连通图?对非连通图给出其连通分量。
正确答案:
(1)所有的简单环:(同一个环可以任一顶点作为起点)
(a)1231
(b)无
©1231、2342、12341
(d)无
(2)连通图:
(a)、©、(d)是连通图,
(b)不是连通图,因为从1到2没有路径。具体连通分量为:

2
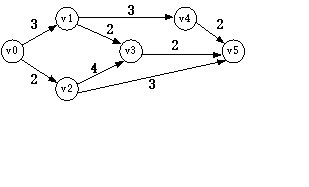
(1) 该图是强连通的吗? 若不是,则给出其强连通分量。
(2) 请给出所有的简单路径及有向环。
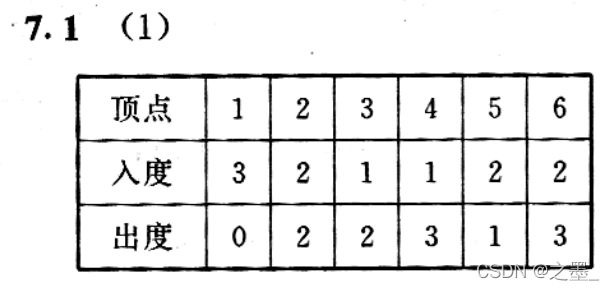
(3) 请给出每个顶点的度,入度和出度。
正确答案:
(1)该图是强连通的
所谓强连通是指有向图中任意顶点都存在到其他各顶点的路径
(2)简单路径是指在一条路径上只有起点和终点可以相同的路径:
有v1v2、v2v3、v3v1、v1v4、v4v3、v1v2v3、v2v3v1、v3v1v2、v1v4v3、v4v3v1、v3v1v4
另包括所有有向环,有向环如下:
v1v2v3v1、v1v4v3v1(这两个有向环可以任一顶点作为起点和终点)
(3)每个顶点的度、入度和出度:
D(v1)=3 ID(v1)=1 OD(v1)=2
D(v2)=2 ID(v2)=1 OD(v2)=1
D(v3)=3 ID(v3)=2 OD(v3)=1
D(v4)=2 ID(v4)=1 OD(v4)=1
1
在一个具有n个顶点的无向连通图中至少有( )条边
正确答案:
第一空: n-1
2
设G是一个含有6个顶点的无向图,该图至多有( )条边
正确答案:
第一空: 15
3
在一个具有n个顶点的有向图中,构成强连通图时至少有( )条边
正确答案:
第一空: n
4
非空无向图的邻接矩阵是一个( )。
正确答案:
第一空: 对称矩阵
5
一个图的邻接矩阵是对称矩阵,则该图是( )。
正确答案:
第一空: 无向图或有向图
6
在含有n个顶点e条边的不带权无向图的邻接矩阵中,零元素的个数为( )
正确答案:
第一空: n2-2e
6
在含有n个顶点e条边的不带权无向图的邻接矩阵中,零元素的个数为( )
正确答案
第一空: n2-2e
7
一个图的邻接表表示中有奇数个边结点,则该图是( )
正确答案:
第一空: 有向图
8
如果从无向图的任一顶点出发进行一次广度优先遍历即可访问所有顶点,则该图一定是( )
正确答案:
第一空: 连通图
9
对有n个顶点、e条边且使用邻接表存储的有向图进行深度优先遍历,其算法的时间复杂度是( )
正确答案:
第一空: O(n+e)
10
对有n个顶点、e条边且使用邻接矩阵存储的有向图进行广度优先遍历,其算法的时间复杂度是( )
正确答案:
第一空: O(n2)
11
在用邻接表表示图时,拓扑排序算法时间复杂度为( )。
(A) O(n) (B) O(n+e) © O(nn) (D) O(nn*n)
正确答案:
第一空: B
12
设无向图的顶点个数为n,则该图最多有( )条边。
(A)n-1 (B)n(n-1)/2 ©n(n+1)/2 (D) n2
正确答案:
第一空: B
13
无向图G=(V,E),其中:V={a,b,c,d,e,f},E={(a,b),(a,e),(a,c),(b,e),(c,f),(f,d),(e,d)},对该图进行深度优先遍历,得到的顶点序列正确的是( )
(A)a,b,e,c,d,f (B)a,c,f,e,b,d ©a,e,b,c,f,d (D)a,e,d,f,c,b
正确答案:
第一空: D
3
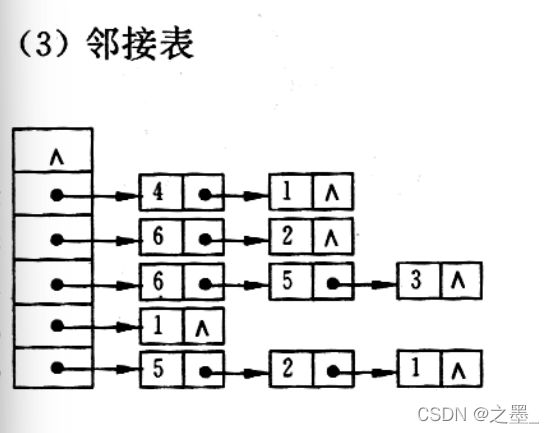
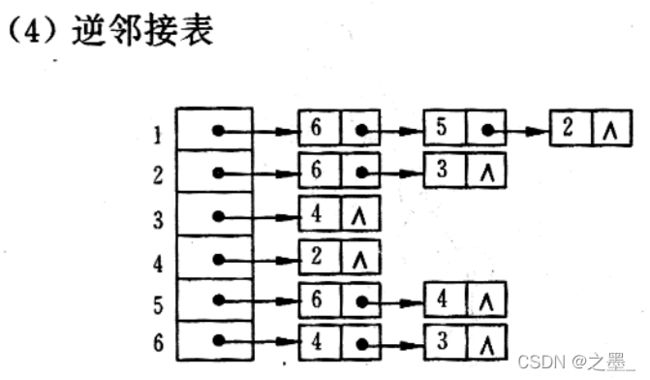
对n个顶点的有向图G,采用邻接表存储,请回答下列有关问题:
(1)如何求图中的边数?
(2)如何判断顶点i到顶点j是否有边相连?
(3)如何求任意一个顶点i的入度?
正确答案:
答案:
(1)累加每个边单链表中的结点个数即为边数
(2)判断第i个边单链表中是否有顶点j的结点,若有表示顶点i到顶点j有边,否则没有边
(3)扫描所有边单链表,累加顶点i的结点个数即为顶点i的入度
我的答案:
对于有向图用邻接表存储时:
(1)边数就等于 邻接表中 边表中的边结点的个数 即若边结点个数为n 边数为 n
(2)可观察顶点 i 的邻接边表 若它的adjvex域有另一顶点位置结点,则表示有一条 i 到j 的边 j到i同理
(3)任意一个顶点的出度就等于该顶点的边表中结点的个数 入度则要遍历各个顶点的边表,若存在i顶点则个数+1 最终得到总个数
4
对于稠密图和稀疏图,采用邻接矩阵和邻接表哪个更好些?
正确答案:
答案:邻接矩阵适合于稠密图,因为其存储空间与边数无关。邻接表适合于稀疏图,因为其存储空间与边数有关,边数越多,存储空间越大。
我的答案:
稠密图用邻接矩阵存储更好 稀疏图用邻接表存储更好
因为邻接矩阵需要存储所有的结点信息 非零结点和零结点均会被存储 邻接表只存储非零结点
稀疏图的非零结点较少 用邻接表存储效率更高 用稠密图会造成空间的浪费 所以稀疏图用邻接表存储
稠密图的非零结点多而零结点较少 所以稠密图用邻接矩阵能更高效利用空间
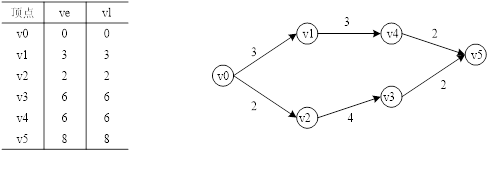
5
AOE网G如下所示,求关键路径。(要求标明每个顶点的最早发生时间和最迟发生时间,并画出关键路径)
(1)最早发生时间和最迟发生时间: (2)关键路径:
6
对n个顶点的无向图和有向图,采用邻接矩阵和邻接表表示时,如何判别下列有关问题?
(1) 图中有多少条边?
(2)任意两个顶点i和j是否有边相连?
(3) 任意一个顶点的度是多少?
正确答案:
对于n个顶点的无向图和有向图,用邻接矩阵表示时:
(1)设m为矩阵中非零元素的个数 无向图的边数=m/2 有向图的边数=m
(2)无论是有向图还是无向图,在矩阵中第i行,第j列的元素若为非零值,则该两顶点有边相连。
(3)对于无向图,任一顶点i的度为第i行中非零元素的个数。
对于有向图,任一顶点i的入度为第i列中非零元素的个数,出度为第i行中非零元素的个数,度为入度出度之和。 当用邻接表表示时:
(1)对于无向图,图中的边数=边表中结点总数的一半。 对于有向图,图中的边数=边表中结点总数。
(2)对于无向图,任意两顶点间是否有边相连,可看其中一个顶点的邻接表,若表中的adjvex域有另一顶点位置的结点,则表示有边相连。
对于有向图,则表示有出边相连。 (3)对于无向图,任意一个顶点的度则由该顶点的边表中结点的个数来决定。
对于有向图,任意一个顶点的出度由该顶点的边表中结点的个数来决定,入度则需遍历各顶点的边表。(用逆邻接表可容易地得到其入度。)
我的答案:
无向图:
邻接表:
(1)
边数等于边结点的个数➗2
(2)
顶点i的G->adjlist[i]为头结点的单链表中若有j的边表结点则i和j有边相连
(3)
顶点i的度等于 G->adjlist[i]为头结点的单链表中边表结点的个数
邻接矩阵:
(1)
图的边数等于邻接矩阵中为1的元素个数➗2
(2)
邻接矩阵的g.edgs[i][j]若为非零,则代表i和j有边相连否则无边相连
(3)
顶点i的度等于第i行中非零元素的个数
有向图:
邻接表:(1)
边数等于边结点个数
(2)
从头结点为G->adjlist[i]的单链表中找到编号为j的边表结点,说明i到j有边,对应的从G->adjlist[j]同理
(3)
顶点i的出度等于g->adjlist[i]为头结点的单链表中边表结点的个数,入度则遍历所有边结点,G->adjlist[j]为头结点的单链表中有i则顶点i的入度+1,度数等于入度和出度之和
邻接矩阵:
(1)
图的边数等于邻接矩阵中非零和非∞的元素个数
(2)
g.edgs[i][j]为非0和非∞则表示i到j有边 e.edgs[j][i]则表示j到i有边
(3)
顶点i的出度等于第i行中元素为非0非∞的个数 入度等于第i列非0非∞元素个数
7
n个顶点的连通图至少有几条边?强连通图呢?
正确答案:
n个顶点的连通图至少有n-1条边,强连通图至少有2(n-1)条边。