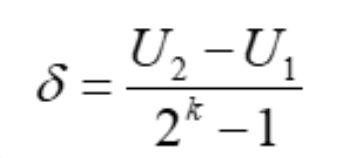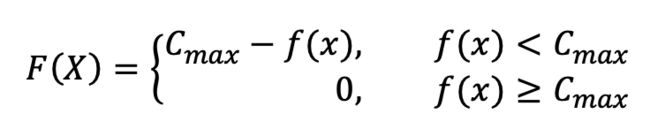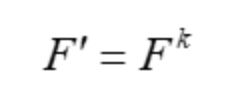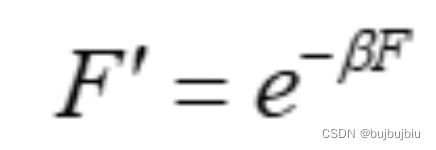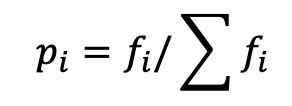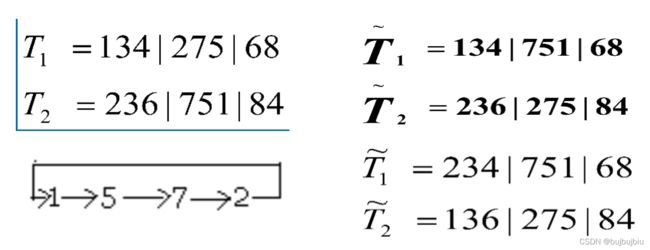遗传算法GA原理及实现（python实现GA求解TSP代码）

目录

1.遗传算法描述

1.1遗传算法构成要素

1.2遗传算法流程

2.遗传算法设计

2.1编码与解码

 2.2适应度函数

 2.3选择算子

 2.4交叉算子

 2.5变异算子

2.6初始化种群

2.7算法终止

3.GA求解TSP(python)

---

1.遗传算法描述

遗传算法（Genetic Algorithms,GA）是1962年由美国Michigan大学的Holland教授提出的模拟自然界遗传机制和生物进化论而成的一种并行随机搜索最优化方法。

遗传算法将“优胜劣汰，适者生存”的生物进化原理引入优化参数形成的编码串联群体中，按所选择的适应度函数并通过遗传中的复制、交叉及变异对个体进行筛选，使适适应度高的个体被保留下来，组成新的群体，新的群体既继承了上一代的信息，又优于上一代。这样周而复始，群体中个体适应度不断提高，直到满足一定的条件。遗传算法的算法简单，可并行处理，并能到全局最优解。

在遗传算法中,染色体应的是数据或数组,通常是由一维的串结构数据来表示,串上各个位置对应基因的取值。基因组成的串就是染色体，或者称为基因型个体(individuals)。一定数量的个体组成了群体(population)。群体中个体的数目称为群体大小(populationsize)，也称为群体规模。而各个个体对环境的适应程度叫做适应度(fitness)

1.1遗传算法构成要素

（1）染色体编码

群体中的个体使用固定长度的二进制符号串表示，初始群体中各个个体的基因值用均匀分布的随机数生成，如X：100111001000101101表示一个个体，其染色体长度为18。

（2）个体适应度评价

按与个体适应度成正比的概率来决定当前群体中每个个体遗传到下一代群体中的机会多少。适应度函数是非负的，而目标函数有负有正，因此需要预先确定好由目标函数值到个体适应度之间的转换规则

（3）遗传算子

• 选择运算：比例选择算子
• 交叉运算：单点交叉算子
• 变异运算：基本位变异算子

（4）运行参数

遗传算法可定义为一个元组：

• M：群体大小，即群体中个体数量，一般取20-100
• T：遗传运算的终止进化代数，一般取100-500
• F：个体适应度评价函数
• s,c,m：选择操作算子，交叉操作算子，变异操作算子
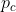• ：交叉概率，一般取0.6～0.99
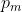• ：变异概率，一般取0.005～0.01

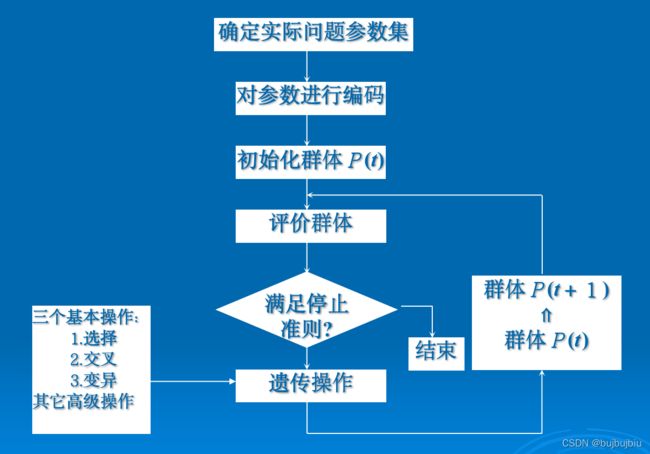
1.2遗传算法流程

（1）选择编码策略，把参数集合Ｘ和域转换为相应编码空间Ｓ

（2）定义适应值函数

（3）定义遗传策略，包括选择群体大小、选择、交叉、变异方法以及确定交叉概率、变异概率等遗传参数

（4）随机初始化生成群体Ｐ(t)

（5）计算群体中个体的适应值 

（6）按照遗传策略，运用选择、交叉和变异操作作用于群体，形成下一代群体

（7）判断群体性能是否满足某一指标，或者已完成预定迭代次数，不满足则返回步骤（6），或者修改遗传策略再返回步骤（6）

2.遗传算法设计

2.1编码与解码

（1）编码

从问题的解(solution)到基因型的映射称为编码，即把一个问题的可行解从其解空间转换到遗传算法的搜索空间的转换方法。遗传算法在进行搜索之前先将解空间的解表示成遗传算法的基因型串(也就是染色体)结构数据，这些串结构数据的不同组合就构成了不同的点。常见的编码方法有二进制编码、实数编码，格雷码编码、 浮点数编码、各参数级联编码、多参数交叉编码等。

• 二进制编码：假设某参数的取值范围为，用长度为k二进制编码符号串来表示该参数，则总共能产生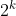种不同的编码，参数编码时对应关系如下：

 其中为二进制编码精度，公式为：

例子：变量x的定义域为[－2，5]，要求其精度为。  

需将[－2，5]分成至少7 000 000个等长小区域，而每个小区域用一个二进制串表示。 于是串长至少等于23，这是因为： 。这样，计算中的任何一个二进制串都对应[-2，5]中的一个点。  

• 实数编码：对于问题的变量是实向量的情形，可直接采用十进制进行编码，这样可以直接在解的表现形式上进行遗传操作，便于引入与问题领域相关的启发式信息以增加系统的搜索力。 

例子：作业调度问题（JSP）

种群个体编码常用m×n的矩阵（n为从加工开始的天数，m为工件的优先顺序）。表示工件在第日的加工时间。下表是一个随机生成的个体所示。 

• 有序编码： 对很多组合优化问题，目标函数的值不仅与表示解的字符串中各字符的值有关，而且与其所在字符串中的位置有关。这样的问题称为有序问题。若目标函数的值只与表示解的字符串中各字符的位置有关而与其具体的字符值无关，则称为纯有序问题，如采用顶点排列的旅行商问题。

例子： TSP

有10个城市的TSP问题，城市序号为{1，2，…，10}，则编码位串表示对城市采用按序号升序方法访问行走路线。 1   3   5   7   9   2   4   6   8    10 表示按特定 “1 →3 →5 →7 →9 →2 →4 →6 →8 →10 →1” 依次访问各个城市。

•  结构式编码：对很多问题其更自然的表示是树或图的形式，这时采用其它形式的变可能很困难。这种将问题的解表达成树或图的形式的编码称为结构式编码。

 （2）解码

假设一个染色体的编码为，对应解码公式为

 2.2适应度函数

适应度值非负。适应度函数表明个体或解的优劣性。对于不同的问题，适应度函数的定义方式不同。根据具体问题，计算群体P(t)中各个个体的适应度。将目标函数值变成个体适应度

（1）目标函数最大值的优化：为一个适当相对比较小的数

 （2）目标函数最小值的优化：为一个适当相对比较大的数字

 选取方法：预先指定的一个较小（大）的数；进化到当前代为止的最小（大）目标函数值；当前代或最近几代群体中的最小（大）目标函数值。

适应度尺度变换是指算法迭代的不同阶段，能够通过适当改变个体的适应度大小，进而避免群体间适应度相当而造成的竞争减弱，导致种群收敛于局部最优解。适应度尺度变换包括线性尺度变换、乘幂尺度变换以及指数尺度变换。

（1）线性尺度变换：a为比例系数，b为平移系数，F为变换前适应度尺度，变换后适应度尺度

（2）乘幂尺度变换：将原适应度尺度F取k次幂

（3）指数尺度变换

 2.3选择算子

选择算子：从当前代群体中选择出一些比较优良的个体，并将其复制到下一代群体中。选择原则有适应值比例，排名，局部竞争机制。

常用选择算子：比例选择算子，指个体被选中并遗传到下一代群体中的概率与该个体的适应度大小成正比。

比例选择算子方法：轮盘选择。个体适应度越高，被选中的概率越大

——个体被选中的概率

——个体的适应度 

——群体累加适应度

 2.4交叉算子

交叉算子：从种群中随机选择两个个体，通过两个染色体的交换组合，把父串的优秀特征遗传给子串，从而产生新的优秀个体。

常用交叉算子：单点交叉算子 。

单点交叉算子方法：对群体中的个体进行两两随机配对；每一对相互配对的个体，随机设置某一基因座之后的位置为交叉点；对每一对相互配对的个体，依设定的交叉概率 pc 在其交叉点处相互交换两个个体的部分染色体，从而产生出两个新的个体。

其它交叉算子：双点交叉，多点交叉，均匀交叉（每个位置都以等概率进行交叉），算术交叉

 交叉检测：有时交叉会产生不合法的个体，如何保证所产生的个体合法？一种方法是为参与交换的数增加一个映射，将该映射应用于未交换的等位基因即可。

例子：设城市数的旅行商问题，对两个个体进行交叉，中间竖线表示交叉点。得到的下一代个体不是合法的（存在圈），为参与交换的数增加一个映射，将此映射应用于未交换的等位基因得到的个体是合法的

 2.5变异算子

变异算子：对于基本遗传算法中用二进制编码符号串所表示的个体，若需要进行变异操作的某一基因座上的原有基因值为 0 ，则变异操作将该基因值变为 1 ，反之，若原有基因值为 1 ，则变异操作将其变为 0 。

常见变异算子：基本位变异算子

方法：对个体的每一个基因座，依变异概率指定其为变异点；对每一个指定的变异点，对其基因值做取反运算或用其它等位基因值来代替， 从而产生出一个新的个体。

2.6初始化种群

初始群体中的个体一般是随机产生的。 我们往往希望在问题解空间均匀采样，随机生成一定数目的个体（为群体规模的2倍，即2n），然后从中挑出较好的个体构成初始群体。 对于二进制编码，染色体位串上的每一位基因在{0，1}上随机均匀选择，所以群体初始化至少需要L×n次随机取值。

2.7算法终止

（1）预先规定最大演化代数

（2）连续多代后解的适应值没有明显改进，则终止

（3）达到明确的解目标，则终止。

3.GA求解TSP(python)

（1）编码：整数排列编码，对于n个城市的TSP问题，染色体为n段，每一段为对应城市的编号，如10个城市的TSP问题{0,1,2,3,4,5,6,7,8,9)，则[1 3 8 2 0 6 4 7 5 9]为一个合法的染色体。

（2）解码：获取每个个体对应城市的横坐标line_x和纵坐标line_y

（2）适应度函数：设走遍n个城市的总距离为dis，则设置适应度函数为

（3）按照适应度函数比值选择个体即轮盘选择

（4）交叉：对个体A：[1 3 8 2 0 6 4 7 5 9]随机判断每个点是否交叉：[False  True  True False  True False  True False False  True]，保留False对应的城市keep：[1 2 6 7 5]，选择另一个交叉个体B：[4 8 0 6 5 9 1 2 3 7]，判断B中不在keep里的城市：[ True  True  True False False  True False False  True False]，选择True为交换城市swap：[4 8 0 9 3]，将keep和swap连接起来成为新的个体：[1 2 6 7 5 4 8 0 9 3]

（5）变异：对每个点生成随机概率与变异概率比较判断是否需要变异，随机找到另一个变异点，交换两点的数值，如[7 4 6 0 1 5 9 3 2 8]变异后变成[7 4 0 6 1 5 8 3 2 9]，位置3,4和位置7,9变异

（6）进化：依照适应度函数对初始群体进行整体选择，依次对每个个体进行交叉和变异，更新群体

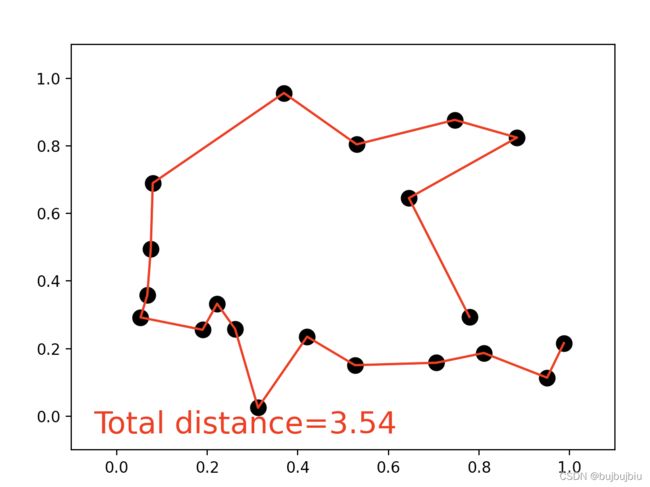
（7）主函数：给定初始种群和城市坐标进行解码获取坐标数据，计算每个个体的总距离和适应度函数，通过适应度函数进化，找到每一次进化适应度函数最高的个体索引，绘图并显示总距离

以下代码来自莫烦python，其中一些numpy用法见numpy笔记（vstack，random.permutation，empty_like，empty，diff，random.choice，random.randint，isin）_bujbujbiu的博客-CSDN博客

import numpy as np
import matplotlib.pyplot as plt

class GA(object):
    def __init__(self,chrom_size,corss_rate,mutation_rate,pop_size):
        self.chrom_size = chrom_size # 染色体长度
        self.cross_rate = corss_rate # 交叉概率
        self.mutate_rate = mutation_rate # 变异概率
        self.pop_size = pop_size # 种群大小
        self.pop = np.vstack([np.random.permutation(chrom_size) for i in range(pop_size)]) # 初始种群编码

    # 解码
    def translate(self,city_position):
        line_x = np.empty_like(self.pop,dtype=np.float64)
        line_y = np.empty_like(self.pop,dtype=np.float64)
        for i,d in enumerate(self.pop): # 按顺序遍历一个解的城市
            city_coord = city_position[d] # 记录城市的坐标
            line_x[i,:] = city_coord[:,0] # 城市的横坐标，shape(pop_size,city_number)
            line_y[i,:] = city_coord[:,1] # 城市的纵坐标，shape(pop_size,city_number)
        return line_x,line_y

    # 适应度函数
    def fitness(self,line_x,line_y):
        total_distance = np.empty((line_x.shape[0],),dtype=np.float64)
        for i,(x,y) in enumerate(zip(line_x,line_y)):
            total_distance[i] = np.sum(np.sqrt(np.square(np.diff(x))+np.square(np.diff(y)))) # 计算每个解的总距离,shape(pop_size,)
        fitness = np.exp(self.chrom_size*2/total_distance) # 计算适应度函数,shape(pop_size,)
        return fitness,total_distance

    # 选择
    def select(self,fitness):
        index = np.random.choice(np.arange(self.pop_size),size=self.pop_size,replace=True,p=fitness/fitness.sum()) # 按适应度函数进行选择
        return self.pop[index]

    # 交叉
    def crossover(self,parent,pop):
        if np.random.rand() < self.cross_rate:
            other = np.random.randint(0,self.pop_size,1) # 另一个交叉个体
            cross_point = np.random.randint(0,2,self.chrom_size,dtype=np.bool) # 交叉点
            keep_city = parent[~cross_point] # parent中留下来的城市
            swap_city = pop[other,np.isin(pop[other].ravel(),keep_city,invert=True)] # other中不在keep_city里的其它城市
            parent[:] = np.concatenate((keep_city,swap_city)) # 连接两个部分变成新个体
        return parent

    # 变异
    def mutate(self,child):
        for point in range(self.chrom_size): # 对于每个个体的点
            if np.random.rand() < self.mutate_rate:
                swap_point = np.random.randint(0,self.chrom_size) # 找到变异点
                swapA,swapB = child[point],child[swap_point] # 交换两点的数值
                child[point],child[swap_point] = swapB,swapA
        return child

    # 进化
    def evolve(self,fitness):
        pop = self.select(fitness)
        pop_copy = pop.copy()
        for parent in pop:
            child = self.crossover(parent,pop_copy)
            child = self.mutate(child)
            parent[:] = child
        self.pop = pop

class TSP(object):
    def __init__(self,city_number):
        self.city_position = np.random.rand(city_number,2)
        plt.ion()

    def plot(self,lx,ly,total_dis):
        plt.cla()
        plt.scatter(self.city_position[:,0].T,self.city_position[:,1].T,s=100,c='k')
        plt.plot(lx.T,ly.T,'r-')
        plt.text(-0.05, -0.05, "Total distance=%.2f" % total_dis, fontdict={'size': 20, 'color': 'red'})
        plt.xlim((-0.1,1.1))
        plt.ylim((-0.1,1.1))
        plt.pause(0.01)

city_number = 20
cross_rate = 0.1
mutate_rate = 0.09
pop_size = 500
generations = 500

GA_TSP = GA(city_number,cross_rate,mutate_rate,pop_size)
env = TSP(city_number)
for gen in range(generations):
    lx,ly = GA_TSP.translate(env.city_position)
    fitness,total_dis = GA_TSP.fitness(lx,ly)
    GA_TSP.evolve(fitness)
    best_index = np.argmax(fitness)
    print('gen:',gen,'|best fitness:%.2f'%fitness[best_index])
    env.plot(lx[best_index],ly[best_index],total_dis[best_index])
plt.ioff()
plt.show()