遗传算法解决TSP问题
一.原理及问题描述
1.遗传算法原理
遗传算法的概念简单来说,就是利用种群搜索技术将种群作为一组问题解,通过对当前种群施加类似生物遗传环境因素的选择、交叉、变异等一系列的遗传操作来产生新一代的种群,并逐步使种群优化到包含近似最优解的状态。
2.TSP问题描述
TSP问题,即旅行商问题,是指对于给定的n个城市,旅行商从某一城市出发不重复的访问其余城市后回到出发城市,要求找出一条路线,路程最短。
3.用遗传算法解决TSP问题思路
3.1 问题的表示
路径表示是表示旅程对应的基因编码的最自然,最简单的表示方法。它在编码,解码,存储过程中相对容易理解和实现。例如:旅程(5-1-7-8-9-4-6-2-3)可以直接表示为(5 1 7 8 9 4 6 2 3)
3.2 交叉运算
一般有以下三种交叉方式
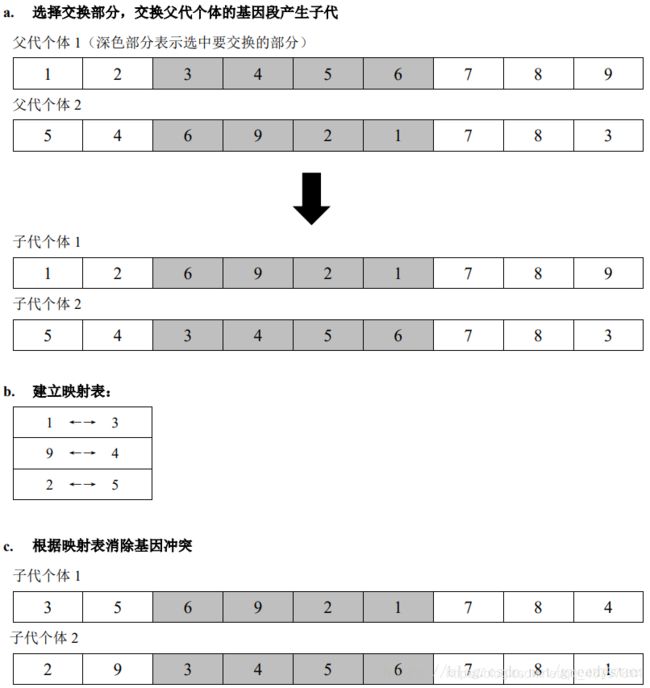
- Partial-Mapped Crossover(部分映射交叉)
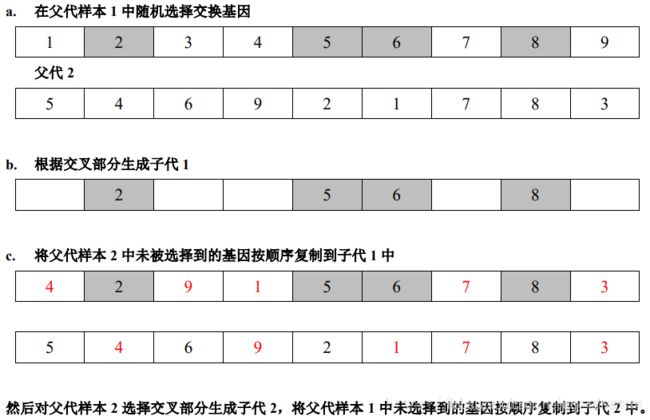
- Order Crossover(顺序交叉)
- Position-based Crossover(基于位置的交叉)
本算法
- 先确定两个城市序列中进行交换的城市
- 交换城市时,若城市序列中包含重复城市,则增加一个交换操作
交叉函数
function [A,B]=cross(A,B)
L=length(A);
if L<10
W=L;
elseif ((L/10)-floor(L/10))>=rand&&L>10
W=ceil(L/10)+8;
else
W=floor(L/10)+8;
end
%%W为需要交叉的位数
p=unidrnd(L-W+1);%随机产生一个交叉位置
%fprintf('p=%d ',p);%交叉位置
for i=1:W
x=find(A==B(1,p+i-1));
y=find(B==A(1,p+i-1));
[A(1,p+i-1),B(1,p+i-1)]=exchange(A(1,p+i-1),B(1,p+i-1));
[A(1,x),B(1,y)]=exchange(A(1,x),B(1,y));
end
end
3.3 变异运算
变异算子随机进行多次,每次在个体基因序列中选择两个位置的基因进行交换。
即直接将同一序列中的两个城市进行交换。
变异函数
function a=Mutation(A)
index1=0;index2=0;
nnper=randperm(size(A,2));
index1=nnper(1);
index2=nnper(2);
%fprintf('index1=%d ',index1);
%fprintf('index2=%d ',index2);
temp=0;
temp=A(index1);
A(index1)=A(index2);
A(index2)=temp;
a=A;
end
3.4 适应度函数
遗传算法在进化搜索中基本不利用外部信息,仅以适应度函数为依据,利用种群中每个个体的适应度值来进行搜索。
%适应度函数fit.m,每次迭代都要计算每个染色体在本种群内部的优先级别,类似归一化参数。越大约好!
function fitness=fit(len,m,maxlen,minlen)
fitness=len;
for i=1:length(len)
fitness(i,1)=(1-(len(i,1)-minlen)/(maxlen-minlen+0.0001)).^m;
end
二.代码脚本
clear;
clc;
%%%%%%%%%%%%%%%输入参数%%%%%%%%
N=25; %%城市的个数
M=100; %%种群的个数
ITER=2000; %%迭代次数
%C_old=C;
m=2; %%适应值归一化淘汰加速指数
Pc=0.8; %%交叉概率
Pmutation=0.05; %%变异概率
%%生成城市的坐标
pos=randn(N,2);
%%生成城市之间距离矩阵
D=zeros(N,N);
for i=1:N
for j=i+1:N
dis=(pos(i,1)-pos(j,1)).^2+(pos(i,2)-pos(j,2)).^2;
D(i,j)=dis^(0.5);
D(j,i)=D(i,j);
end
end
%%生成初始群体
popm=zeros(M,N);
for i=1:M
popm(i,:)=randperm(N);%随机排列,比如[2 4 5 6 1 3]
end
%%随机选择一个种群
R=popm(1,:);
figure(1);
scatter(pos(:,1),pos(:,2),'rx');%画出所有城市坐标
axis([-3 3 -3 3]);
figure(2);
plot_route(pos,R); %%画出初始种群对应各城市之间的连线
axis([-3 3 -3 3]);
%%初始化种群及其适应函数
fitness=zeros(M,1);
len=zeros(M,1);
for i=1:M%计算每个染色体对应的总长度
len(i,1)=myLength(D,popm(i,:));
end
maxlen=max(len);%最大回路
minlen=min(len);%最小回路
fitness=fit(len,m,maxlen,minlen);
rr=find(len==minlen);%找到最小值的下标,赋值为rr
R=popm(rr(1,1),:);%提取该染色体,赋值为R
for i=1:N
fprintf('%d ',R(i));%把R顺序打印出来
end
fprintf('\n');
fitness=fitness/sum(fitness);
distance_min=zeros(ITER+1,1); %%各次迭代的最小的种群的路径总长
nn=M;
iter=0;
while iter<=ITER
fprintf('迭代第%d次\n',iter);
%%选择操作
p=fitness./sum(fitness);
q=cumsum(p);%累加
for i=1:(M-1)
len_1(i,1)=myLength(D,popm(i,:));
r=rand;
tmp=find(r<=q);
popm_sel(i,:)=popm(tmp(1),:);
end
[fmax,indmax]=max(fitness);%求当代最佳个体
popm_sel(M,:)=popm(indmax,:);
%%交叉操作
nnper=randperm(M);
% A=popm_sel(nnper(1),:);
% B=popm_sel(nnper(2),:);
%%
for i=1:M*Pc*0.5
A=popm_sel(nnper(i),:);
B=popm_sel(nnper(i+1),:);
[A,B]=cross(A,B);
% popm_sel(nnper(1),:)=A;
% popm_sel(nnper(2),:)=B;
popm_sel(nnper(i),:)=A;
popm_sel(nnper(i+1),:)=B;
end
%%变异操作
for i=1:M
pick=rand;
while pick==0
pick=rand;
end
if pick<=Pmutation
popm_sel(i,:)=Mutation(popm_sel(i,:));
end
end
%%求适应度函数
NN=size(popm_sel,1);
len=zeros(NN,1);
for i=1:NN
len(i,1)=myLength(D,popm_sel(i,:));
end
maxlen=max(len);
minlen=min(len);
distance_min(iter+1,1)=minlen;
fitness=fit(len,m,maxlen,minlen);
rr=find(len==minlen);
fprintf('minlen=%d\n',minlen);
R=popm_sel(rr(1,1),:);
for i=1:N
fprintf('%d ',R(i));
end
fprintf('\n');
popm=[];
popm=popm_sel;
iter=iter+1;
%pause(1);
end
%end of while
figure(3)
plot_route(pos,R);
axis([-3 3 -3 3]);
figure(4)
plot(distance_min);
三. 结果分析和结论
1.结果分析
以下是城市的个数 N=25;
种群的个数 M=100;
迭代次数 ITER=2000;
适应值归一化淘汰加速指数 m=2;
交叉概率 Pc=0.8;
变异概率 Pmutation=0.05;
随机产生城市坐标得出的结果
首先画出这25个城市的坐标,以及各城市之间的连线,然后
由此发现,随机产生城市坐标不易于定向分析其他参数对此算法的影响
故,优化算法将随机生成的城市坐标储存导入使用
N=25;
citys=randn(N,2);
save citys.mat
在此基础上,我们尝试修改其他变量来分析结果:
<1>
以下是城市的个数 N=25;
种群的个数 M=100;
迭代次数 ITER=2000;
适应值归一化淘汰加速指数 m=2;
交叉概率 Pc=0.8;
变异概率 Pmutation=0.05 时的结果
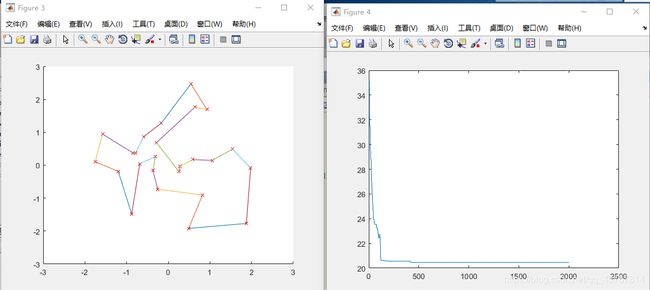
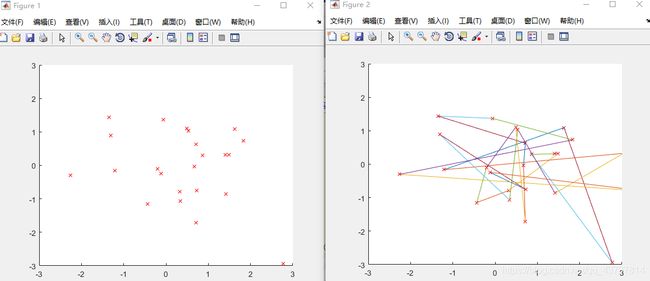
 图1是城市的坐标分布,一共25个城市,图2是初始种群的路线,图3即最终的最短路线,图4是迭代2000次的路径总长的变化,
图1是城市的坐标分布,一共25个城市,图2是初始种群的路线,图3即最终的最短路线,图4是迭代2000次的路径总长的变化,
最短路径:
23 1 25 24 2 4 21 13 7 22 3 6 11 14 16 17 5 8 15 20 10 9 12 18 19
最短长度为24.03694。
<2>
以下是城市的个数 N=25;
种群的个数 M=200;
迭代次数 ITER=2000;
适应值归一化淘汰加速指数 m=2;
交叉概率 Pc=0.8;
变异概率 Pmutation=0.05



图1是城市的坐标分布,一共25个城市,图2是初始种群的路线,图3即最终的最短路线,图4是迭代2000次的路径总长的变化
最短路径:
19 18 12 9 10 15 8 17 16 6 11 14 25 1 24 2 23 22 3 7 5 13 20 21 4
最短长度为:25.21108
为简便设计以下表格
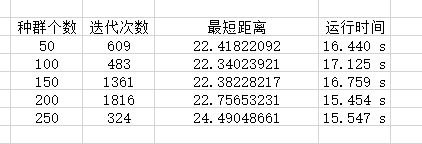
种群个数改变时
由此可知,种群数量增加时,路径总长达到收敛时的迭代次数并不成正比,而是大体先增后减,迭代次数与运行时间也不成正比,说明适当的种群数量有利于加快运行时间和计算最短路径,由我的数据可大约推测出最优种群数量区间为【150,250】。
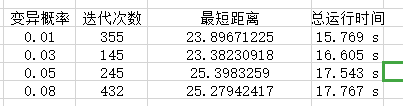
变异概率改变时,随着变异概率的增加,迭代次数先减少再增加,运行时间相反,在变异概率在【0.01,0.03】时较佳。
2.结论
由于遗传算法的整体搜索策略和优化计算是不依赖梯度信息,只需要影响搜索方向的目标函数和相应的适应度函数,所以它的应用比较广泛。利用遗传算来进行大规模问题的组合优化是一种比较有效的方法。但是遗传算法也有不足之处,它对算法的精确度、可行度、计算复杂性等方面还没有有效的定量分析方法。通过本文的算法也可以清晰地认识到,遗传算法所求得的解不一定是最优解。