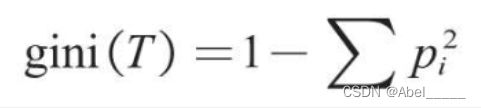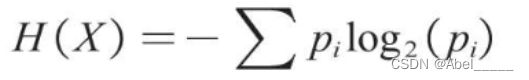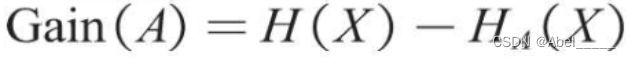决策树算法学习

1、决策树简介

决策树（decision tree）：是一种基本的分类与回归方法，此处主要讨论分类的决策树。

决策树通常有三个步骤：特征选择、决策树的生成、决策树的修剪。

在分类问题中，表示基于特征对实例进行分类的过程，可以认为是if-then的集合，也可以认为是定义在特征空间与类空间上的条件概率分布。

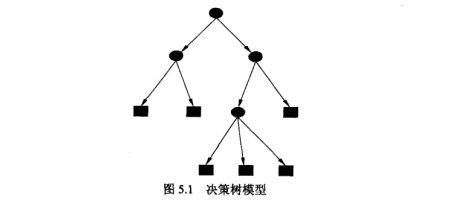
用决策树分类：从根节点开始，对实例的某一特征进行测试，根据测试结果将实例分配到其子节点，此时每个子节点对应着该特征的一个取值，如此递归的对实例进行测试并分配，直到到达叶节点，最后将实例分到叶节点的类中。

下图为决策树示意图，圆点——内部节点，方框——叶节点

 决策树的概念并不复杂，主要是通过连续的逻辑判断得出最后的结论，其关键在于如何建立这样一棵“树”。

2、Gini系数（CART决策树）

决策树模型的建树依据主要用到的是基尼系数的概念。

采用基尼系数进行运算的决策树也称为CART决策树。

基尼系数（gini）用于计算一个系统中的失序现象，即系统的混乱程度（纯度）。基尼系数越高，系统的混乱程度就越高（不纯），建立决策树模型的目的就是降低系统的混乱程度（体高纯度），从而得到合适的数据分类效果。

基尼系数的计算公式如下。

其中pi为类别i在样本T中出现的频率，即类别为i的样本占总样本个数的比率。

 当引入某个用于分类的变量（如“满意度＜5”）时，分类后的基尼系数公式如下。

 其中S1、S2为划分后的两类各自的样本量，gini（T1）、gini（T2）为两类各自的基尼系数。

3、信息熵、信息增益

除了基尼系数，还有另一种衡量系统混乱程度的经典手段——信息熵。

在搭建决策树模型时，信息熵的作用和基尼系数是基本一致的，都可以帮助合理地划分节点。

信息熵H(X)的计算公式如下。

其中X表示随机变量，随机变量的取值为X1，X2，X3…，在n分类问题中便有n个取值，例如，在员工离职预测模型中，X的取值就是“离职”与“不离职”两种；pi表示随机变量X取值为Xi的发生频率，且有Σpi＝1。

为了衡量不同划分方式降低信息熵的效果，还需要计算分类后信息熵的减少值（原系统的信息熵与分类后系统的信息熵之差），该减少值称为熵增益或信息增益，其值越大，说明分类后的系统混乱程度越低，即分类越准确。

基尼系数涉及平方运算，而信息熵涉及相对复杂的对数函数运算，因此，目前决策树模型默认使用基尼系数作为建树依据，运算速度会较快。

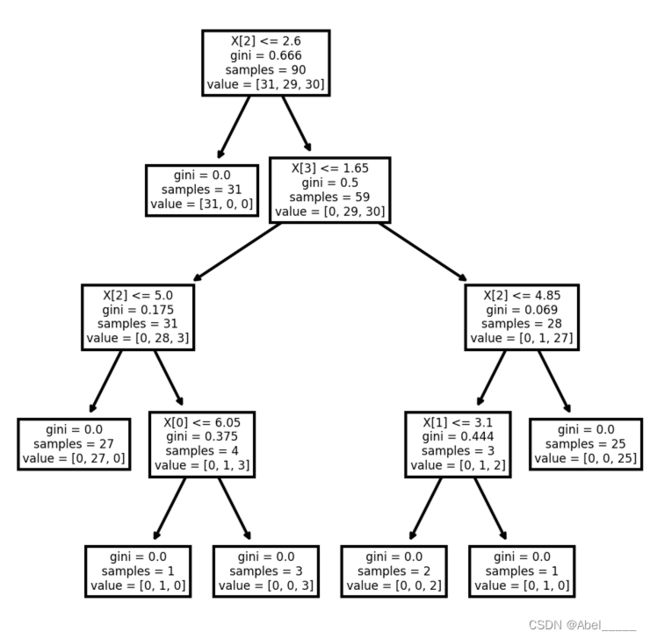
4、具体实现

首先导入鸢尾花(Iris)数据集

通过sklearn中的决策树算法来构建决策树，分类树用到DecisionTreeClassifier函数实现，criterion是判断先构建哪个节点的标准，可以选择gini或者entropy；选择entropy就是通过信息增益来选择先判断的节点；选择gini则是计算基尼系数来判断

iris = load_iris()
X_train, X_test, y_train, y_test = model_selection.train_test_split(iris.data, iris.target, test_size=0.4, random_state=1)
model = tree.DecisionTreeClassifier(criterion='gini',splitter='best',max_depth=7)
model.fit(X_train,y_train)
score = model.score(X_test,y_test)

 最后通过可视化生成鸢尾花(Iris)决策树

 5、实验总结

        通过这次实验对决策树有了更深入的了解，决策树说通俗点就是一棵能够替我们做决策的树，或者说是我们人类在要做决策时脑回路的一种表现形式，对连续值的处理，了解了背后算法的原理就是先进行排序然后再不断的进行二分，比较熵值选出最优的，剪枝分为预剪枝和后剪枝，预剪枝比较简单就是通过设置树的最大深度和节点数来提前进行限制