VAE：变分自编码器的理解与实现

VAE理解与实现

1. 理解VAE

VAE是一类生成模型，其假设在低维空间(维度k,k)中存在一个关于输入X(维度d)的真实概率分布：$p_{gt}(x)$。现考虑一个与X相关的潜在变量z(维度d)，z的分布为$p(z)$，通常也称之为先验分布（通常为正态分布），因此可重写概率分布$p_{gt}(x)$：

先验分布是我们事先设定的，已知的

从上式我们可以明白，只要我们能够找到$p_{gt}(x|z)$，那么就能利用其生成新样本（先从先验分布采样z，再根据$p_{gt}(x|z)$采样生成新的X）：

从而期望利用最大似然估计来求解 $P_{\theta }=\left\{p_{\theta }(x|z)|\theta \right\}$：

但是上面这个式子在数学上是很难求解的，因此VAE构造了一个新的概率分布$q(z|x)$，也称之为编码分布(encoder distribution)，现在重写最大似然估计：

类似于EM算法的分解

按行进行分析：
第1行没啥好说的，就是离散值的极大似然估计；
第2行在$logP(x)$中引入编码分布$q(z|x)$，其积分后与左式相等；
第3行进行一些变换，引入$P(z,x)$与$P(z|x)$；
第4行拆分log函数，相乘变相加，其中后一项即为$q(z|x)$与$P(z|x)$之间的KL散度（其值永远大于等于0）；
第5行即为第4行前一项，因为KL散度≥0，因此$logP(x)$存在一个下界，称之为lower bound Lb(也称为ELBO (Evidence Lower BOund) )。

这里借用了李宏毅老师的PPT，其中P(x)就表示之前提到的真实分布$p_{gt}(x)$

现在我们知道$logP(x)$可以拆分为ELBO与KL散度这两项，然后我们又期望整个数据集上的$logP(x)$都最大，如何优化呢？既然极大似然估计不好做，那么我们就去优化ELBO，想办法让他变大，并且让$logP(x)$也随之变大。

由于P(z)是已知的先验分布，这里采用P(x|z)与q(z|x)联合优化使得Lb最大，为什么要用两项联合优化呢？

假设我们现在只用P(x|z)去最大化Lb，但我们并不知道KL(q(z|x)||P(z|x))如何变化，因此不知道最终的似然是否上升。

如果我们固定P(x|z)，仅使用q(z|x)优化Lb，我们知道P(x)与q(z|x)无关，因此最终似然大小固定，随着Lb变大，因此KL(q(z|x)||P(z|x))变小，如下图所示：

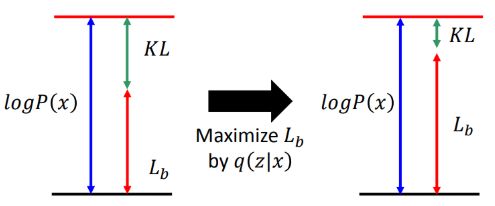
所以这里使用P(x|z)与q(z|x)联合优化使得Lb最大，最后理想的结果KL会接近于0，Lb变大，那么$logP(x)$也会随之增大，同样q(z|x)也解决与P(z|x)。

现在，我们明确了目标是优化Lb，现在重写Lb表达式：

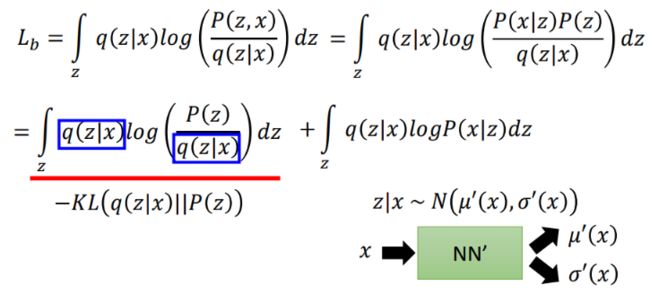
还是将式子进行一些转换，从而转换为两项，其中前一项为-KL(q(z|x)||P(z))，这一项永远≤0。因此优化目标进一步变为最小化KL(q(z|x)||P(z))以及最大化后一项：

其中前一项中的$q(z|x)$为编码分布，并假设其为多元高斯分布(GMM角度)，使用一个神经网络来根据输入x，预测与z相关的高斯分布的均值与方差，而P为我们的先验分布，通常为正态分布，现在进行推导。

由于VAE考虑的是各分量独立的多元正太分布，因此只需要推导一元正态分布的情形即可，图片与推导来自https://zhuanlan.zhihu.com/p/34998569

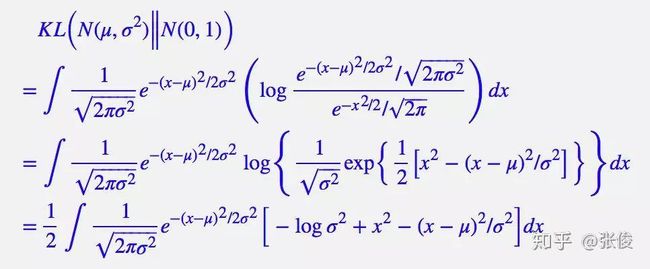
整个结果分为三项积分，第一项实际上就是 $-log{\sigma }^2$ 乘以概率密度的积分（也就是 1），所以结果是 $-log{\sigma }^2$；第二项实际是正态分布的二阶矩，熟悉正态分布的朋友应该都清楚正态分布的二阶矩为 ${\mu }^2+{\sigma }^2$；而根据定义，第三项实际上就是“-方差除以方差=-1”。因此总的结果为：

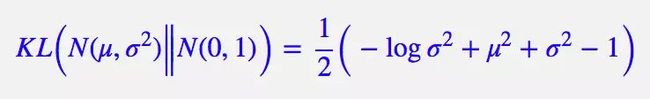
因此，网络中所用到的损失函数也就为下式（也称之为KLD loss），这里需要特别注意下式中的${\delta }_i$是方差的log，而上式中的${\delta }^2$是方差，博主比较懒就不自己写推导了，所以在看的时候，大家自己转换一下：

这一块可以对应着代码消化，为什么模型输出要是log方差呢？这是因为方差一定大于0，而模型的输出有可能小于0，加上exp操作之后，其永远大于0，并以此作为最终的方差。

其次，最大化后一项其实就是根据q(z|x)最大化$log(P(x|z))$，意思就是根据q(z|x)我们能够采样得到z，然后根据得到的这个z能够很好地重现出x，这就是普通的Auto-Encoder在做的事情，计算生成样本与真实样本之间的MSE Loss：

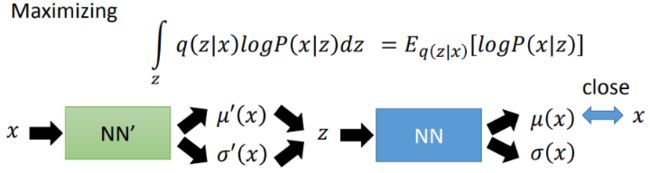
李宏毅，从GMM角度解释VAE ：https://www.youtube.com/watch?v=8zomhgKrsmQ&t=2780s，强烈推荐

自此，整个VAE的结构就很清晰了，为了数据生成，我们引入了一个额外的先验分布p(z)，并引入新分布q(z|x)并让其逼近p(z)，从而缩小KL散度，这也构成了VAE的第一部分损失：KLD-Loss。另一部分就是最大化logP(x|z)，即对分布q(z|x)进行抽样得到z能够很好重构输入，构成了第二部分损失：MSE-Loss。

由于编码器，解码器都是用的神经网络，这里没有用EM算法求解，而是直接采用梯度下降的方法进行优化，同时优化两个目标，从而找到最优解。训练完的VAE，编码器输出分布q(x|z)非常接近p(z)，从该分布采样的值也能很好地重构输入样本，而p(z)就是标准正态分布。因此直接从正态分布p(z)中采样，然后送入解码器中即可生成新样本，并且生成的样本与输入样本也非常相似。

2. 模型实现

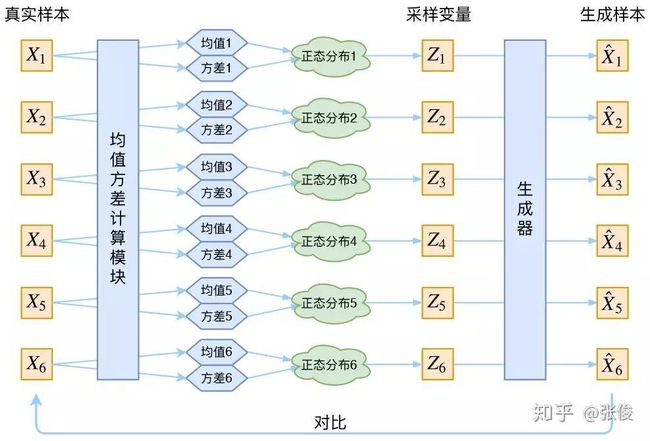
根据之前的推导，每个样本x首先送入encoder中，计算得到q(z|x)对应均值、方差，这确定了其分布（高斯混合模型），并且我们期望这个分布逼近于先验分布P(z)[通常是正态分布]，这一部分计算得到KLD loss。得到分布之后，我们从q(z|x)分布采样变量得到z，送到decoder中生成样本，然后根据生成样本与真实样本计算MSE loss。

图片来自https://zhuanlan.zhihu.com/p/34998569

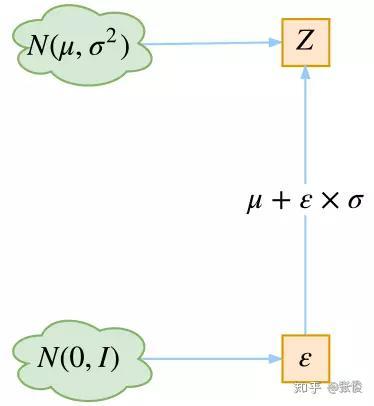
但我们注意，要把这个模型训练起来，通常采用的是梯度下降的方法。而根据分布进行采样的过程我们无法求导，这也就导致不能训练，所以在实现中采用了一个叫做Reparameterization的技巧。其核心就是：要从分布为 $N(\mu ,{\delta }^2)$ 采样得到一个值Z，相当于我们从标准正态分布$N(0,1)$中采样一个值$\epsilon$，$Z=\mu +\epsilon \times \delta$，这样，采样的过程就不会参与到反向传播的过程中，使得整个模型能够正常训练。

3. 代码

完整代码见（欢迎issue与star）：https://github.com/Classmate-Huang/CV_GenerateModel/tree/master/VAE

代码共实现了两种VAE，并在MNIST上进行实验，这里以卷积自编码器的构建为例，介绍代码：

def ConvBnRelu(channel_in, channel_out):
	# Conv + BatchNorm + ReLU 模块
    conv_bn_relu = nn.Sequential(
        nn.Conv2d(channel_in, channel_out, 3, stride=2, padding=1),
        nn.BatchNorm2d(channel_out),
        nn.LeakyReLU(0.2, inplace=True)
    )
    return conv_bn_relu


def DConvBnRelu(channel_in, channel_out):
	# Conv + BatchNorm + ReLU 模块
    d_conv_bn_relu = nn.Sequential(
        nn.ConvTranspose2d(channel_in, channel_out, 3, stride=2, padding=1, output_padding=1),
        nn.BatchNorm2d(channel_out),
        nn.LeakyReLU(0.2, inplace=True)
    )
    return d_conv_bn_relu


class VariationAutoEncoder(nn.Module):
    ''' Conv VAE '''
    def __init__(self, in_channel=3, img_size=512, latent_dim=256):
        super().__init__()
        # 编码器
        self.encoder = nn.Sequential(
            ConvBnRelu(in_channel, 96),
            ConvBnRelu(96,128),
            ConvBnRelu(128, 256),
            ConvBnRelu(256, 256),
        )
        # 解码器
        self.decoder = nn.Sequential(
            DConvBnRelu(256, 256),
            DConvBnRelu(256, 128),
            DConvBnRelu(128,96),
            # nn.ConvTranspose2d(96, 3, 3, stride=2, padding=1, output_padding=1),
            DConvBnRelu(96, 96),
            nn.Conv2d(96,in_channel, kernel_size=3, padding=1),
            nn.Tanh()
        )
		# latent code的维度
        self.latent_dim = latent_dim
        self.img_size = img_size
        original_dim = 256*(img_size//16)**2
        # 将原始code的维度映射至指定维度
        self.fc_mu = nn.Linear(original_dim, latent_dim)
        self.fc_var = nn.Linear(original_dim, latent_dim)
        # 用于恢复分辨率
        self.fc_recover = nn.Linear(latent_dim, original_dim)
        
    def reparameterize(self, mu, logvar):
    	''' Reparameter技巧 '''
        std = torch.exp(0.5 * logvar)	# std
        eps = torch.randn_like(std)	# 从正态分布中采样
        return eps * std + mu	# 得到

    def forward(self, x):
        # encode 编码阶段
        fea = self.encoder(x)
        fea = torch.flatten(fea, start_dim=1)
        
        # split into mu an var components of the latent Gaussian distribution
        # 将编码结果转换成正态分布的mu与log_var
        mu = self.fc_mu(fea)
        log_var = self.fc_var(fea)

        # get latent code
        # 使用重参数技巧进行采样得到code
        z = self.reparameterize(mu, log_var)

        # decode
        # 将code送入解码器进行解码，解码前需要恢复到原分辨率
        fea = self.fc_recover(z).view(-1, 256, self.img_size//16, self.img_size//16)
        out = self.decoder(fea)

        return mu, log_var, out
    
    def sample(self, num_sample, device):
		''' sampling '''
		# 从标准正态分布中采样 （经过训练，q(z|x)接近标准正态分布）
        z = torch.randn(num_sample, self.latent_dim).to(device)
        # 解码生成样本
        fea = self.fc_recover(z).view(-1, 256, self.img_size//16, self.img_size//16)
        out = self.decoder(fea)

        return out

实验结果
① 重构效果：

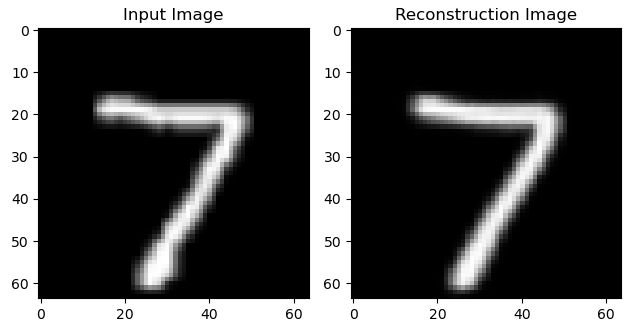
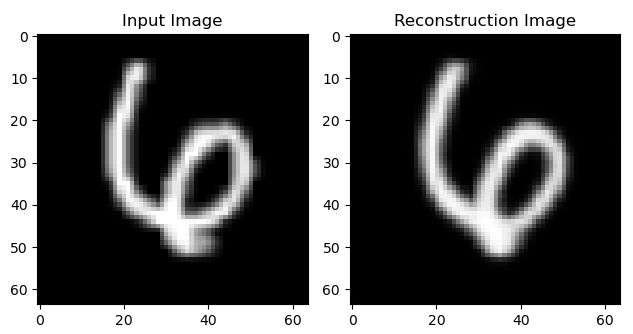
② 生成效果：

4. 总结

VAE的本质是找到一个先验分布p(z)与样本空间的真实概率分布p(x)之间的联系，从而根据p(x|z)生成新样本。乍一看确实很难下手，所以VAE额外引入分布q(z|x)，并且这个分布是基于神经网络(编码器)得到的（生成均值方差，从而确定一个分布）。让q(z|x)去逼近p(z)，然后同时让q(z|x)这个分布中采样值能够重构输入样本x，使得$E_{q(z|x)}logP(x|z)$最大，从而使得ELBO上升，整体似然上升。

这也体现了生成模型的一个特点，通过训练数据去建模数据的真实分布，然后再根据这个模型与分布生成更多的数据。

从某个角度上理解，VAE相比于AE在重构过程中在latent code上引入了高斯噪声，并且让Latent Code满足某种分布，使得我们利用分布采样生成code，生成新样本。

参看李宏毅老师的VAE讲解：https://www.youtube.com/watch?v=8zomhgKrsmQ&t=2780s

对于初学者，VAE的确很难理解，但随着了解的深入，你会发现其设计与思想（ELBO、Reparameter trick）真的非常的巧妙，让人不得不感叹数学的魅力。VAE目前也存在大量的变种模型，被广泛应用于各领域。