超分之ESPCN

这篇文章推出了一种具有亚像素卷积层结构的SR算法——ESPCN；相比于SRCNN直接对$HR$领域像素做卷积，ESPCN是直接对输入$LR$像素做特征提取，在当时来说，可以算是一种提高计算效率的有效途径。

参考文档：
①:【超分辨率】Efficient Sub-Pixel Convolutional Neural Network

Abstract

文章推出了一种在以往算法(SRCNN、Bicubic)上对于重建表现力以及计算效率(重建速度、计算资源损耗)都有一定提升的SR算法——ESPCN。
SRCNN先对输入图像做Bicubic插值，然后进行特征提取，这种方式相当于直接在HR层面做超分，作者证明这种方式是一种次优策略且会带来计算复杂度的提升。

针对这种问题，作者提出了ESPCN结构：

1. 这是一种直接对输入$LR$图像做特征提取。
2. 在网络中引入了一种亚像素卷积层，该层通常为网络的最后一层，它以之前特征提取后的feature map为输入，通过学习一个上采样滤波器来做到$LR\to SR$的重。
3. 直接对$LR$图像做卷积取代了SRCNN中的bicubic预处理部分，这直接带了计算复杂度的降低以及执行速度的提升，作者实现了在1080P视频中的超分效果，做到了标题中的”Real-Time“。
4. ESPCN在图像和视频上都做了相关的实验，分别提升了0.15dB以及0.39dB；此外ESPCN的执行速度也超越了之前的CNN-based系列SR算法。

Note：

1. 这篇文章的核心，也是最重要的部分就是一个亚像素卷积层。

1 Introduction

ESPCN主要2个点很重要：①是直接对$LR$层级图像进行特征提取，②就是一个亚像素卷积层，下面展开来说下：

1. ESPCN直接对$LR$层级的图像进行卷积提取特征，因此我们可以采用一个较小的滤波器去整合不同level的特征信息，相比于SRCNN，这种做法不仅减小了训练参数，同时也降低了计算的复杂度，减少了训练时间。此外，正如DCSCN这篇论文中所说的，在$r\ge 3$的时候，直接对输入图像提取的特征和先用bicubic插值放大之后提取到的特征其实并无差异，因此插值就会显得多余，且浪费计算成本。
2. SRCNN中上采样的方式就是一个简单的处理过程：将输入$LR$图像做插值，只需要一个滤波器即可。而在ESPCN中，假设整个网络有$L$层，那么第$L-1$层产生的$n_{L-1}$张feature map，那么在第$L$层，我们就可以学习一种更复杂的方式，训练$n_{L-1}$个卷积核而不是简单的一个。更重要的是，最后这层可以隐式地去学习这个通道数$n_{L-1}$地滤波器，它本质上就是一个shuffle地过程，将$r^2$张feature map进行整合，这就是亚像素卷积层。

2 Method

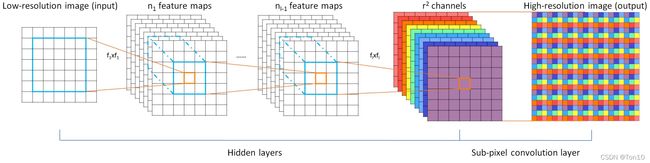
需要注意的是，输入层我们一般定义为第0层，然后下一个卷积层自然就是第一层(”第一层画在卷积过程中，而不是画在输出feature map上“)，然后以此类推，第$L$层就是我们的亚像素卷积层，输出层可以表示为第$L+1$层。

上图就是ESPCN网络结构，接下来对其中几点进行说明：

1. 输入图像是$LR$图像，通道数为$C$，比如RGB格式图像中，$C=3$，我们的目标就是从$C\times H\times W$的图像变成$C\times rH\times rW$的图像。
2. 整个网络分为2部分：特征提取部分，由连续的CNN网络组成；上采样部分，由一个亚像素卷积层构成。
3. 设整个网络一共有$L$层，前$L-1$层通过卷积、非线性激活组成，具体表达式为：$$\begin{gathered} f^1(I^{LR};W_1,b_1)=\varphi (W_1\ast I^{LR}+b_1) \\ {f}^l(I^{LR};W_{1:l},b_{1:l})=\varphi (W_l\ast f^{l-1}(I^{LR})+b_l). \end{gathered}$$其中$W_l,b_l,l\in (1,L-1)$是滤波器的参数；$\varphi (\cdot )$是激活函数；$f^L$就是亚像素卷积层。
4. 特征提取层保持图像的大小不变。
5. 卷积层参数$W_l$表示为：$n_{l-1}\times n_l\times k_l\times k_l$，$n_l$表示当前第$l$层有$n_l$个滤波器，也就是输出$n_l$张feature map；$n_{l-1}$是上一层有$n_{l-1}$个滤波器，也就是当前第$l$层输入的feature map张数；特别的，$n_0=C$，这也是我们一些深度学习库中卷积层的设置方式，比如PyTorch。

2.1 Deconvolution layer

Deconvolution layer主要分为三个方面：

1. 非监督学习，比如这篇文章Adaptive Deconvolutional Networks for Mid and High Level Feature Learning所介绍的一种反卷积结构。
2. CNN可视化。
3. 上采样。比如FCN网络中介绍的deconvolution layer是一种将低分辨率的图像还原成高分辨率图像的方法。

我们在SR中所用到的反卷积层大多都是用几层CNN处理的，比如DCSCN、SRDenseNet、SRGAN、SRResNet、EDSR，详见我的几篇论文解读。

2.2 Efficient sub-pixel convolution layer

FCN网络中最后3层改以往的全连接层为反卷积层，其本质也是个卷积层，故称之为Fully-convolution(具体内容详见我的另一篇中关于FCN的笔记)。诸如FCN这种反卷积过程是一种上采样过程，它可以将低分辨率尺寸的图像转换为高分辨率尺寸的图像，因此这种卷积可以看成是卷积步长为$\frac{1}{r}$的运算过程。但是这种方式往往需要在反卷积成$HR$图像之后再接一个$stride=1$的CNN层才会有较大的性能提升，但对$HR$图像做卷积似乎又回到SRCNN的问题，间接增加了计算复杂度。

---

因此作者提出了一种同样以$\frac{1}{r}$为步长，但不需要额外计算量的隐式卷积层——亚像素卷积层(sub-pixel convolution layer)。接下来我们从宏观和微观两个角度去理解这一个过程。

①首先从宏观上来看：
宏观上可以将亚像素卷积层看成是一个像素Shuffle的过程：将$r^2$张feature map组成的张量进行size变型和像素重组，有点类似于PyTorch中的reshape或者view的过程，Shuffle简单来说就是一个从$r^{2}C\times H\times W$到$C\times rH\times rW$的过程，通过这种方式产生$rW\times rH$的高分辨率图像。而亚像素卷积层也是这个原理，这不过size转型再重组的过程和reshape不一样，reshape是按照数组的底层实现来重组像素，那么亚像素卷积是怎么做的呢？具体如下图所示：
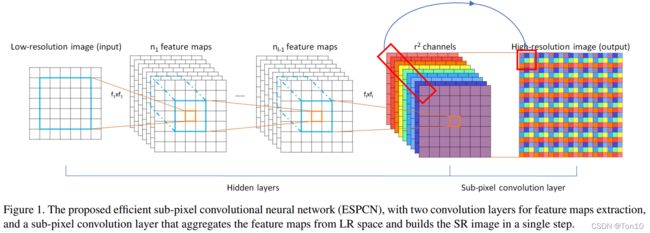它将不同通道上同一个位置的$r^2$像素(如红色斜矩形所示)排列成$3\times 3$的形状来作为输出$HR$像素的一个块(如红色小框所示)，然和对于所有不同通道同一位置的$r^2$个像素都这样做，就形成了上图最后的$HR$图像，可以看到整体分辨率放大了$r=3$倍。
Note：

1. 上述展示的就是PyTorch中torch.nn.PixelShuffle(r)展示的做法。
2. 我们再来总结一下宏观理解背后怎么做的：卷积核$k_s$相当于变型成一个和上图斜红矩形框一样的形状，然后抽取出这些像素(特征)。也就是说一共有$r^2$个特征，这样就是纵向一次卷积的过程(需要注意的是说的是卷积，但其实没有进行运算，只是抽取出来然后进行简单排列)。按照这样的方式继续进行下去，如上图所示，进行$7\times 7=49$次之后就完成了亚像素卷积的过程。至于到底抽取的是哪一纵列，那么需要取决于像素点在$HR$图像中的位置$mod(x,r)、mod(y,r)$，其中$x,y$是$HR$图像中位置。

②然后从微观上来看：
一、为什么叫亚像素卷积？
微观上可以将亚像素卷积层看成是一个隐式卷积的过程：隐式卷积的意思就是还是会用一个滤波器去抽取信息，但是和传统的卷积运算不同，这里并没有涉及可学习的滤波器参数以及任何乘加运算。如上图所示，亚像素卷积过程中从左到右的过程就好像以一个$stride=\frac{1}{r}$对$LR$图像做卷积，从而在直观上好像卷积生成出了一些小小的像素点，又因为$\frac{1}{r}\le 1$，意味着它做的是整像素内部的运算，我们称之为亚像素，比如视频处理中常见的$\frac{1}{2}、\frac{1}{4}$像素都是亚像素。
二、亚像素卷积是如何工作的？
接下来我们具体来看亚像素卷积网络背后的思想：设亚像素卷积层的滤波器为$W_s$，其卷积核的size为$k_s\times k_s$，其中$k_s$满足$mod(k_s,r)=0$(mod是取余函数)，为了方便接下来讨论，我们这里设$k_s=r$。
我们用一个卷积核大小为$k_s\times k_s$的滤波器$W_s$来抽取信息，且步长$stride=\frac{1}{r}$，$weightspacing=\frac{1}{r}$，这里的参数间隔我觉得是空洞卷积中的填充率。那么由于填充个数是个小于1的数，因此我们可以将$W_s$的卷积核表示成如下图：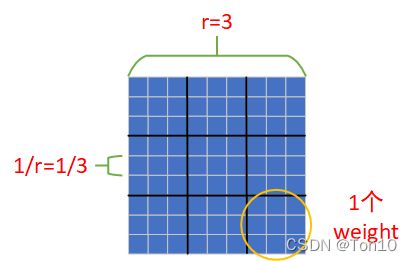
以这样的卷积核，步长$\frac{1}{r}$去做卷积输出的结果就是我们输出层所显示的结果，只不过我们仍不做乘加运算，而是简单抽取信息。

Note：

1. 至于为什么取名为Periodic Shuffle，是因为单纯看颜色而忽略像素值的话，每个pattern(图中一个$r^2$个颜色小块)在$LR$种被不断循环激活(就是提取特征，参与某种运算)，输出到$HR$中，具体对哪个pattern做卷积，要去取决于$mod(x,r),mod(y,r)$，其中$(x,y)$是$HR$层级中的坐标。
2. 从整个过程来看，亚像素卷积的过程并不改变像素的个数，即抽取$r^2$个，输出也是$r^2$个像素。
3. 从第一部分可知，亚像素卷积可以看成是以$\frac{1}{r}$为步长进行特征提取，那么也就意味着卷积核$k_s$相邻参数的距离一定也是$\frac{1}{r}$。
4. 上图卷积核黑色线之间的小卷积方块参数都是不参与计算的(not activated)，只是单纯提取特征。
5. 这个变换虽然被称作sub-pixel convolution, 但实际上并没有卷积操作。
6. 我们提取的目标就是上图中9($r^2$)种颜色的特征信息，也就是文中的$r^2$个activation pattern。我们每做一次$k_s\times k_s$的卷积，都需要激活$r^2$个特征信息，故每个特征信息需要$\lceil \frac{k_s}{r}{\rceil }^2=1$个参数。

---

理解了Periodic-Shuffle的过程之后，我们就可以其引入数学表达了：
整个亚像素卷积过程可以看成是一个映射：
$$I^{SR}=f^L(I^{LR})=\mathcal{P}\mathcal{S}(W_L\ast f^{L-1}(I^{LR})+b_L).\text{\hspace{1em}(1)}$$，其中$\mathcal{P}\mathcal{S}(\cdot )$是一个算子，其定义的运算如下：
$$\mathcal{P}\mathcal{S}(T{)}_{x,y,c}=T_{[x/r],[y/r],C\cdot r\cdot mod(y,r)+C\cdot r\cdot mod(x,r)+c}.\text{\hspace{1em}(2)}$$
Note：

1. 我们定义亚像素卷积层(第$L$层)的参数为$W_L、b_L$，它的size为$r^{2}C\times 1\times k_L\times k_L$(这里论文中公式应该写错了，论文中的是$n_{L-1}\times r^{2}C\times k_L\times k_L$)，其中$k_L=\frac{k_s}{r}$，这地方可以这样理解，$k_L$所表达的是卷积核再2D平面上的size，而上述我们描述的$k_s$是从亚像素卷积层面考虑的，并且$W_s$在做的时候可以将其看成是空洞卷积的形式，因此根据卷积公式，其也可以近似看成是滤波器大小为$\frac{k_s}{r}$的卷积运算：
   ，故他们两表达的其实都是一个意思。在这里$k_L=\frac{k_s}{r}=\frac{r}{r}=1$，我们只从平面来考虑卷积运算的话，其实就是对单个像素做运算，而深度信息$r^2$放到了滤波器的通道上，这其实反应的背后思想就是我们上述的宏观理解，通过一个纵向的卷积核去提取出$r^2$个像素信息，这也是特征提取的一种措施，只不过不涉及通常卷积的乘加运算。
2. 亚像素卷积层之后是不加任何激活函数的，该层之后就是输出层。
3. 在式(2)中，$x,y,c$是在$HR$中的坐标；$[\cdot ]$表示取商，因此$[x/r]、[y/r]$表示在$LR$图像哪一个整像素，即平面坐标；而$C\cdot r\cdot mod(y,r)+C\cdot r\cdot mod(x,r)+c$表达的就是在纵向深度(通道)上的哪一个整像素，即深度坐标。因此式(2)表达的就是我们上述宏观上的理解。举个例子，比如$HR$上的坐标为$(2,2)$，我们这里假设$r=3,C=1$(只针对单通道图像)，那么在第一个通道$c=1$处的值就是$2+2+1=5$，然后我们就取出$T_5$的值作为输出$HR$在坐标$(2,2)$处的值。
4. 式(1)表达的就是首先将$L$层的$n_L$张feature map进行像素提取，也就是括号内的卷积过程(乘加操作)；然后用$\mathcal{P}\mathcal{S}$算子进行像素Shuffle操作，最后输出$I^{SR}$。

我们之前说过整个ESPCN一共$L$层，第$L$层是亚像素卷积层，因此式(1)做的就是将第$L-1$层(输出$n_{L-1}$张feature map)的输出经过亚像素卷积(再提一下，这里表面写的是乘加的形式，他其实是不参与计算的，只是隐式的卷积)。而$\mathcal{P}\mathcal{S}(\cdot )$表达的就是亚像素卷积的过程。
Note：

1. 关于亚像素卷积是一个隐式卷积，它是另一种提取特征的过程，不含任何可学习参数，故并不是我们常用的卷积层，文中2处也指明了这一点：
2. 我们画出上述第一点中的②结构：

---

有了亚像素卷积层的输出，我们就可以利用Ground-Truth来做MSE，通过梯度反传更新网络参数来学习如何从低分辨率重建成高分辨率图像：
$$l(W_{1:L},b_{1:L})=\frac{1}{r^{2}HW}\sum _{x=1}^{rH}\sum _{y=1}^{rW}(I_{x,y}^{HR}-f_{x,y}^L(I^{LR}){)}^2.\text{\hspace{1em}(3)}$$作者指出我们的亚像素卷积层可以比FCN的上采样过程快近${\log }_2{r}^2$倍，比SRCNN的bicubic插值上采样过程快近$r^2$倍。

3 Experiments

实验会基于单张图像和视频的形式，对各类算法的PSNR做测试。

3.1 Datasets

1. 图像数据集：Timofte datasets(91张图片)、Set5、Set14、BSD300、BSD500、super texture dataset(136张图片)、ImageNet(5W张图片)。
2. 只考虑YCbCr的Y通道，即亮度通道。
3. 对于每一个up scaling factor，都训练一个specific网络。
4. 视频数据集：Xiph database，包含8份1080p($1920\times 1080$)的视频，每一份长达10s；Ultra Video Group database，包含7份1080p的视频，每份长达5s。

3.2 Implementation details

1. 实验中的ESPCN设置$L=4$层，其中$l=L-1=3$层，滤波器的参数参照于SRCNN的设置，每一层依次是：$(f_1,n_1)=(5,64),(f_2,n_2)=(3,32),(f_3,n_3)=(3,r^2)$。
2. 输入图像的格式为$17\times 17$，来自Ground Truth $I^{HR}$。
3. 激活函数使用$tanh$，后文还和ReLU做了对比试验。
4. 初始学习率设置为0.01，当表现力的提升小于$\mu$的时候，逐渐降低学习率直到$10^{-4}$；而最后一层的学习率要同比衰减10倍。
5. 使用PSNR做图像评价指标。

3.3 Image super-resolution results

3.3.1 Benefits of the sub-pixel convolution layer

上图是为了体现亚像素卷积层的作用，从图中可以得出以下结论：

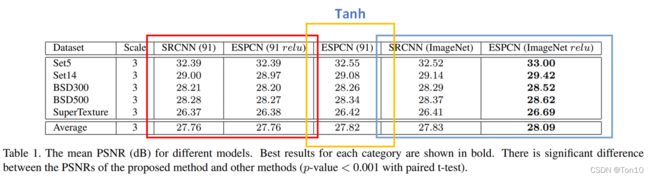
1. 使用了亚像素卷积层的ESPCN(relu)要比SRCNN有更好的表现力。
2. 较大的数据集有利于表现力的提升。
3. 虽然SRCNN和ESPCN(relu)在小数据集上表现相似，但是一旦数据集增大，两者增加的PSNR分别是0.07和0.33，显然ESPCN有更大的提升潜能。
4. 对比ESPCN关于ReLU和Tanh版本的激活函数可知：在ESPCN中，Tanh对于表现力的提升要强于ReLU。

上图是学习过后的滤波器可视化图，其中$C$就是滤波器$W_l$对一些feature map的学习可视化，从图中我们可知：

1. ESPCN的最后一层是亚像素卷积层，从可视化图来看，这个上采样滤波器$W_L$的确学习到了一些复杂多样的参数，为不同的feature map配置不同的滤波器参数，相比SRCNN较为单一的滤波器类型，ESPCN会使得特征的提取更加复杂、全面。

• 这里有个疑问点是最后一层的可视化不知道是怎么做上去的，这可能要涉及到ESPCN的源码。

3.3.2 Comparison to the state-of-the-art

这一节是将ESPCN在ImageNet上做训练，然后和其余几种算法做对比，具体如下表：

此外，可视化的结果如下图所示：

3.4 Video super-resolution results

这一节是将ESPCN和SRCNN等算法在视频上做超分，其实就是对每一帧做图像超分。相比之前的算法，ESPCN具有执行速度上的优势，实验基于3.1节的2个视频数据集，结果如下：

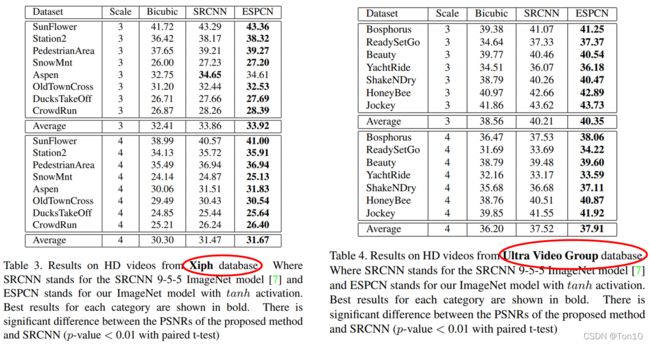
3.5 Run time evaluations

这一节是探究ESPCN在执行速度上和其他算法的差异，作者将几种算法在Set14数据集上测试，其中ESPCN选择最佳的实验模型并使用Tanh做激活函数，在$r=3$下具体实验结果如下所示：

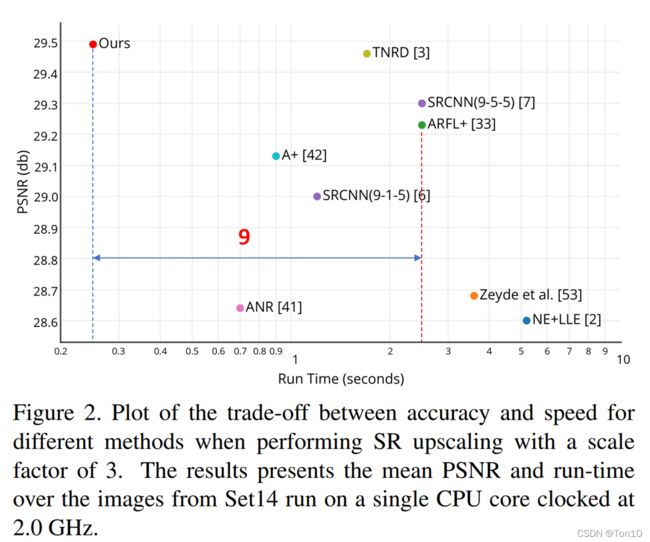
1. 从上图中可以看出，SRCNN的执行速度是ESPCN的9($r^2$)倍，且参数量大约是2.5倍，因此ESPCN的计算复杂度是SRCNN的$\frac{1}{2.5\times r\times r}$倍。
2. 此外，作者在视频中也对2个视频数据集分别进行了检测，其中在$r=3$的时候，SRCNN 9-5-5每一帧消耗0.435s去超分，而ESPCN只需0.038s/帧；在$r=4$的时候，SRCNN需要0.434s/帧，而ESPCN只需0.029s/帧。

4 Conclusion

这篇文章主要有3点需要掌握：

1. 作者证明了类似于SRCNN这种直接对$LR$图像先做bicubic插值，然后进行卷积特征提取的办法会消耗更多的计算资源，因此本文推出的方法并不是直接针对HR层面进行计算，而是直接对输入$LR$层级的图像进行特征提取，这会带来更低的计算损耗；此外，可以使用更小的卷积核提取到合适的特征，从而可以加快训练速度。
2. 文章的核心是提出了一个亚像素卷积层结构，该层位于网络最后一层。亚像素卷积层结构其实就是超分中的上采样部分，但不同于DCSCN、SRDenseNet、SRResNet、EDSR那样使用一个反卷积层来实现$LR\to SR$，亚像素卷积层是去隐式地学习一个上采样滤波器，将$r^2$张feature map在最后一层处进行shuffle，从而产生$rW\times rH$大小的高分辨率图像，这也就意味着这一层并不需要太多额外的训练，一定程度上加快了训练速度。
3. EPSCN最后在单张图像和视频中都取得了提升的效果，分别是0.15dB和0.39dB以及在训练速度上的提升($>\times 10$)。由于ESPCN拥有在LR领域做特征提取以及亚像素卷积层结构，故其网络参数会相对较少，这也为ESPCN在视频中可以做到Real-Time，即实时性的要求。
4. 关于亚像素卷积层，PyTorch中也有相关实现，即torch.nn.PixelShuffle()，具体参考我的另一篇PyTorch之PixelShuffle()。

5 Future work

1. SRCNN是一种SISR方法，而ESPCN可以针对视频做超分。但是ESPCN并没有利用视频中前后相邻帧和当前帧的时间关系，要知道相邻帧种蕴藏着很多和当前帧相关的信息，作者指出接下来需要利用这一时间冗余的关系，时间冗余指的是视频在时间序列上具有相似关系。
2. ESPCN接下来的一个发展方向就是VESPCN，是一种主要针对视频超分的方法，大致的方向就是将ESPCN结构扩展成时序空间网络结构(Spatio-temporal Network)，将时间信息加入到我们的网络中来，因此就有了同一批作者写的"Real-Time Video Super-Resolution with Spatio-Temporal Networks and Motion Compensation"。