[学习笔记] Neuron Networks and Deep Learning
前言
文章内容是基于Micheal Nielsen在 http://neuralnetworksanddeeplearning.com 上提供教程《Neural networks and Deep learning》进行的个人学习理解。方便自己温故而知新,加深理解。
课程开头,Nielsen说明了他写书目的以及对学习者的一些建议,个人的简要理解如下:
1、《Neural networks and Deep learning》讲解了仿生神经网络的结构,数学表达,以及基于此类结构发展出来的深度学习算法。
2、学习此书,求精不求多,修炼内功(数学原理)以及基本的招式(Python数学工具),以能够融会贯通为主要目的。
鉴于Nielsen的建议,作者计划对此书进行精读之后,再进一步寻找基于Pytorch、Tensorflow等深度学习框架的实践练习。再人工智能学习的进程中,同时练习各种经典的机器学习算法,换换思路。毕竟可以预见,Nielse的这本书对我来讲,啃起来还是比较烧脑的;-P,半路出家的表示有些Hard,大家如果有学习建议,也欢迎提出交流~
使用神经网络识别手写数字
通过传统的逻辑判断的方式难以写出程序对手写的数字进行识别,通过机器学习,在此处是神经网络的方式提出了解决思路,通过字体数据的训练,得出模型,进行识别。
![[学习笔记] Neuron Networks and Deep Learning_第1张图片](http://img.e-com-net.com/image/info8/96d74567e3c541d19f7182ef3a9eead9.jpg)
Perceptrons
threshold其实就是bias(参数b),他是一种阀值,用于对‘权重*特征’后的输出结果进行判断。这种解释,让我对bias的理解更加清晰了一些。
![[学习笔记] Neuron Networks and Deep Learning_第3张图片](http://img.e-com-net.com/image/info8/4194194d5abf4d25ada873ea32629b6f.jpg)

Sigmoid Perceptrons
如果我们希望权重的微调可以控制输出的微调,那么上文的Perceptrons是无法实现的,在bias的位置会有0和1的跃变。举个例子,如果需要训练识别数字9,从8训练到9的过程中,各neuron的值会在0和1之间跳变,从而造成其他数字识别效果的剧烈波动。因此,一种柔和的调节思路是必要的,Sigmoid在此处提供了解决方案。
import numpy as np
import matplotlib.pyplot as plt
# Sigmoid数据
x = np.arange(-10,10,0.1)
y_s= 1 / (1 + np.exp(-x))
# StepFunction数据
y_b = []
for i in x:
if i < 0:
num = 0
y_b.append(num)
else:
num = 1
y_b.append(num)
# Plot the results
plt.figure()
plt.plot(x, y_s, c="r", label="Sigmoid", linewidth=2, ls='-')
plt.plot(x, y_b, c="g", label="Step Function", linewidth=2, ls='--')
plt.xlabel("X")
plt.ylabel("Y")
plt.title("Sigmoid and Bias perceptron")
plt.grid()
plt.legend()
plt.show()
神经网络结构
基本的神经网络结构如下图,其由input layer, hidden layer 以及 output layer 构成。input layer 和 output layer结构相对简单,中间的hidden layer则显得千变万化。
![[学习笔记] Neuron Networks and Deep Learning_第5张图片](http://img.e-com-net.com/image/info8/0fa8ac36bd6845a8a9fb0d5531eba6d9.jpg)
以识别手写数字9为例,数字图像由64 x 64 = 4096的灰度值像素组成,则input layer为4096 x 1的一维向量,output为0到1的数字,当output > 0.5,则表明结果为9,越接近1,为9的可能性越大。
神经网络结构多样,此处学习记录的是最简单的一种结构。
一种手写数字识别的神经网络
![[学习笔记] Neuron Networks and Deep Learning_第6张图片](http://img.e-com-net.com/image/info8/fc64b152209044279af485d9834d9589.jpg)
图像已被实现分割好,为28 x 28 = 784的灰度图像,输出为10x1的向量,里面存储了10种结果,即0~9。
梯度下降法(Gradient Descent)
Cost Funtion如下:

寻找 ω \omega ω 和 b b b ,使得 C C C( ω \omega ω, b b b) ≈ \approx ≈ 0 0 0,其中, y ( x ) y(x) y(x) = = = ω T \omega^T ωT x x x + + + b b b。
1、梯度下降法的物理理解:
以 ω \omega ω对应两个特征 x x x的参数为例, C C C( ω \omega ω, b b b) 在三维空间上的形状可以理解如下:
![[学习笔记] Neuron Networks and Deep Learning_第7张图片](http://img.e-com-net.com/image/info8/383404571b2b455e8a5d0bad363899b4.jpg)
ω \omega ω代表的小球的位置不断迭代,直到最低点,小球运动趋势则跟每个位置处 C C C( ω \omega ω, b b b)的梯度相关。
2、梯度下降法的数学理解:
Cost Function的不断下降过程可以用一下公式来表达(因为主要给自己回顾知识用,图方便,直接贴公式图片了):
![[学习笔记] Neuron Networks and Deep Learning_第8张图片](http://img.e-com-net.com/image/info8/8ebf4b9c5c9b443ab1b73022458ae461.jpg)
![[学习笔记] Neuron Networks and Deep Learning_第9张图片](http://img.e-com-net.com/image/info8/099a1ac6cd0e43068366840ac421ebdf.jpg)
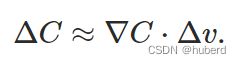
定义:
![[学习笔记] Neuron Networks and Deep Learning_第10张图片](http://img.e-com-net.com/image/info8/cbb25a1000664447b880dcc5051df6c6.jpg)
可以看到,定义了参数 ω \omega ω(截图中为 v v v)沿着梯度的反方向进行迭代,可以保证Cost Function一直减小,直到参数不再变化。因此,从数学的交付,还原了“小球下山”这样一种想象的物理过程。
随机梯度下降
参数 ( ω , b ) (\omega,b) (ω,b)的迭代过程如下:
![[学习笔记] Neuron Networks and Deep Learning_第11张图片](http://img.e-com-net.com/image/info8/f0af486f323c488cacdeec1d875ff67c.jpg)
其中,

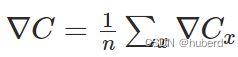
如果样本量很大,及 n n n特别大,则会消耗特别大的计算能力,因此出现了随机梯度下降算法的优化策略,即,设计合适 m m m(mini batch),使得:
![[学习笔记] Neuron Networks and Deep Learning_第12张图片](http://img.e-com-net.com/image/info8/646921c88c13449abdfc0018f4946ee6.jpg)
3、个人对此形象的理解就是:
Cost Function是关于 ( ω , b ) (\omega,b) (ω,b)的函数,训练数据及输出 ( x , a ) (x,a) (x,a)则是Cost Function的系数,系数的数量 n n n越大越全面,Cost Function对于系统误差的描述就越准确,但是同时也会增加计算的难度,因此需要找一组数量不多不少 m m m来描述这个系统的误差,以此兼顾系统误差描述的准确性及计算的高效性。
4、以一个实际的例子打比方:
政府做民意调查,如果每次调整都做全样本的调查则会特别准确,但是耗时耗力,如果每次调整采用抽样调查的形式,则有可能实现又快有准。
随机梯度下降的极端形式为每次迭代只选用一个样本点进行估计,这种情况则有可能导致系统无法收敛。
用代码实现上述方法
代码主体如下:
import numpy as np
import matplotlib.pyplot as plt
import random
import mnist_loader
#### Miscellaneous functions
def sigmoid(z):
"""The sigmoid function."""
return 1.0/(1.0+np.exp(-z))
def sigmoid_prime(z):
"""Derivative of the sigmoid function."""
return sigmoid(z)*(1-sigmoid(z))
# 定义一个神经网络的类
class Network(object):
def __init__(self, sizes):
self.num_layers = len(sizes)
self.size = sizes
self.biases = [np.random.randn(y, 1) for y in sizes[1:]]
self.weights = [np.random.randn(y, x)
for (x, y) in zip(sizes[:-1], sizes[1:])]
def feedforward(self, a):
'''
返回输入a在神经网络中的输出
'''
for b, w in zip(self.biases, self.weights):
a = sigmoid(np.dot(w, a) + b)
return a
def SGD(self, training_data, epochs, mini_batch_size, eta, test_data=None):
if test_data:
n_test = len(test_data)
n = len(training_data)
for j in range(epochs):
# 每次学习(epoch)前,先random一下training_data
random.shuffle(training_data)
# 对training_data按mini_batch_size进行切片,形成一组mini_batchs用于梯度下降的模型评估
mini_batchs = []
for k in range(0, n, mini_batch_size):
mini_batchs.append(training_data[k:k + mini_batch_size])
# 参数迭代
for mini_batch in mini_batchs:
self.updata_mini_batch(mini_batch, eta)
# 结果输出
if test_data:
print('Epoch{0}: {1} / {2}'.format(j, self.evaluate(test_data), n_test))
else:
print('Epoch{0} complete'.format(j))
def updata_mini_batch(self, mini_batch, eta):
nabala_b = []
nabala_w = []
for b in self.biases:
nabala_b.append(np.zeros(b.shape))
for w in self.weights:
nabala_w.append(np.zeros(w.shape))
for x, y in mini_batch:
delta_nabala_b, delta_nabala_w = self.backprop(x, y)
for i in range(len(nabala_b)):
nabala_b[i] = nabala_b[i] + delta_nabala_b[i]
for i in range(len(nabala_w)):
nabala_w[i] = nabala_w[i] + delta_nabala_w[i]
for i in range(len(self.biases)):
self.biases[i] = self.biases[i] - (eta / len(mini_batch)) * nabala_b[i]
for i in range(len(self.weights)):
self.weights[i] = self.weights[i] - (eta / len(mini_batch)) * nabala_w[i]
def backprop(self, x, y):
"""Return a tuple ``(nabla_b, nabla_w)`` representing the
gradient for the cost function C_x. ``nabla_b`` and
``nabla_w`` are layer-by-layer lists of numpy arrays, similar
to ``self.biases`` and ``self.weights``."""
nabla_b = [np.zeros(b.shape) for b in self.biases]
nabla_w = [np.zeros(w.shape) for w in self.weights]
# feedforward
activation = x
activations = [x] # list to store all the activations, layer by layer
zs = [] # list to store all the z vectors, layer by layer
for b, w in zip(self.biases, self.weights):
z = np.dot(w, activation)+b
zs.append(z)
activation = sigmoid(z)
activations.append(activation)
# backward pass
delta = self.cost_derivative(activations[-1], y) * \
sigmoid_prime(zs[-1])
nabla_b[-1] = delta
nabla_w[-1] = np.dot(delta, activations[-2].transpose())
# Note that the variable l in the loop below is used a little
# differently to the notation in Chapter 2 of the book. Here,
# l = 1 means the last layer of neurons, l = 2 is the
# second-last layer, and so on. It's a renumbering of the
# scheme in the book, used here to take advantage of the fact
# that Python can use negative indices in lists.
for l in range(2, self.num_layers):
z = zs[-l]
sp = sigmoid_prime(z)
delta = np.dot(self.weights[-l+1].transpose(), delta) * sp
nabla_b[-l] = delta
nabla_w[-l] = np.dot(delta, activations[-l-1].transpose())
return (nabla_b, nabla_w)
def evaluate(self, test_data):
"""Return the number of test inputs for which the neural
network outputs the correct result. Note that the neural
network's output is assumed to be the index of whichever
neuron in the final layer has the highest activation."""
test_results = [(np.argmax(self.feedforward(x)), y)
for (x, y) in test_data]
return sum(int(x == y) for (x, y) in test_results)
def cost_derivative(self, output_activations, y):
"""Return the vector of partial derivatives \partial C_x /
\partial a for the output activations."""
return (output_activations - y)
- 备注:学习过程中对python的zip()函数理解起来很费劲,自己用for进行了一个替换,测试记录如下:
a = [np.zeros(5),np.zeros(7)]
b = [np.array([1,2,3,4,5]),np.array([1,1,1,1,1,1,1])]
# 使用zip
c = [na+nb for na,nb in zip(a,b)]
print(c)
# 使用for替代,比较输出结果
for i in range(len(a)):
a[i] = a[i] + b[i]
print(a)
输出结果如下,两者结果一致
[array([1., 2., 3., 4., 5.]), array([1., 1., 1., 1., 1., 1., 1.])]
[array([1., 2., 3., 4., 5.]), array([1., 1., 1., 1., 1., 1., 1.])]
运行程序:
import mnist_loader
import network
# 提取数据
training_data, validation_data, test_data = mnist_loader.load_data_wrapper()
# 把Zip格式的数据
training_data = list(training_data)
validation_data = list(validation_data)
test_data = list(test_data)
# 初始化神经网络
net = network.Network([784, 30, 10])
# 梯度下降算法进行参数迭代和模型评估
net.SGD(training_data, 20, 1000, 3.0, test_data=test_data)
*备注:数据的处理与读取通过Nielsen提供的mnist_loader.py模块实现,在此不是学习重点。
运行结果:
本次试验设计了一个三层结构的神经网络,输入层+中间层(1层)+输出层。输入层有784维度,代表28x28的手写图像。输出层有10维输出,代表0~9的结果。
![[学习笔记] Neuron Networks and Deep Learning_第13张图片](http://img.e-com-net.com/image/info8/90567f6d8fdc4688811e333e62cd7e30.jpg) 草稿杂记,用于时间久了忘记了,找回思路:
草稿杂记,用于时间久了忘记了,找回思路:
![[学习笔记] Neuron Networks and Deep Learning_第14张图片](http://img.e-com-net.com/image/info8/8637da09bf254c1e828ccacad9d64630.jpg)
![[学习笔记] Neuron Networks and Deep Learning_第2张图片](http://img.e-com-net.com/image/info8/2fffd54d6a1840e58da7223666af60ac.jpg)
![[学习笔记] Neuron Networks and Deep Learning_第4张图片](http://img.e-com-net.com/image/info8/f709f4937f654c8d96e4afe3777e717f.jpg)