CDMA向量内积的计算
CDMA向量内积的计算
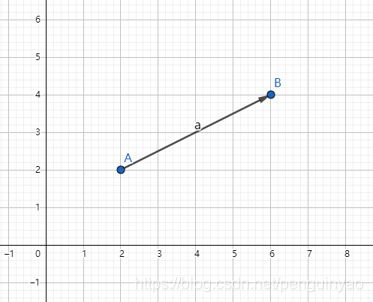
在平面坐标上,有A点和B点,A点坐标是 ( x 1 , y 1 ) (x_{1}, y_{1}) (x1,y1),B点坐标是 ( x 2 , y 2 ) (x_{2}, y_{2}) (x2,y2)。
则
A B → = ( x 2 − x 1 , y 2 − y 1 ) \overrightarrow{AB}=(x_{2}-x_{1},y_{2}-y_{1}) AB=(x2−x1,y2−y1)
那么 A B → \overrightarrow{AB} AB向量的模是
∣ A B ∣ = ( x 2 − x 1 ) 2 + ( y 2 − y 1 ) 2 \left|AB\right|=\sqrt{(x_{2}-x_{1})^2+(y_{2}-y_{1})^2} ∣AB∣=(x2−x1)2+(y2−y1)2
即是线段AB的长度。
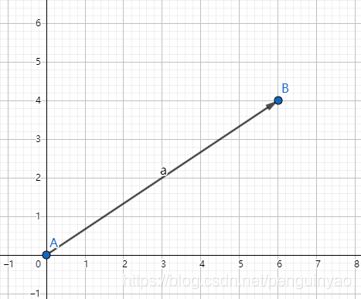
若A点在原点,即 x 1 = 0 x_{1}=0 x1=0, y 1 = 0 y_{1}=0 y1=0,则 A B → = ( x 2 , y 2 ) \overrightarrow{AB}=(x_{2},y_{2}) AB=(x2,y2),如图2所示。
三维空间的向量就是在三维空间的两个点之间的带有方向和大小的量。在三维空间中有A和B点两,A点坐标是 ( x 1 , y 1 , z 1 ) (x_{1}, y_{1},z_{1}) (x1,y1,z1),B点坐标是 ( x 2 , y 2 , z 2 ) (x_{2}, y_{2},z_{2}) (x2,y2,z2)。则
A B → = ( x 2 − x 1 , y 2 − y 1 , z 2 − z 1 ) \overrightarrow{AB}=(x_{2}-x_{1},y_{2}-y_{1},z_{2}-z_{1}) AB=(x2−x1,y2−y1,z2−z1)
其他同理。
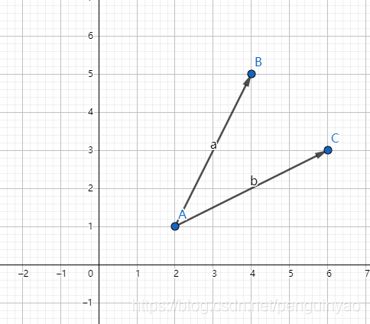
如图3所示,在二维平面上有两个向量 a ⃗ = ( a 1 , a 2 ) \vec{a}=(a_{1},a_{2}) a=(a1,a2), b ⃗ = ( b 1 , b 2 ) \vec{b}=(b_{1},b_{2}) b=(b1,b2),则内积 a ⃗ ⋅ b ⃗ = ∣ a ⃗ ∣ ∣ b ⃗ ∣ cos θ ( 1 ) \vec{a} \cdot \vec{b}=\left|\vec{a}\right|\left| \displaystyle\vec{b}\right|\cos\theta\qquad\qquad\qquad\qquad\qquad(1) a⋅b=∣a∣∣∣∣b∣∣∣cosθ(1)
若 a ⃗ \vec{a} a, b ⃗ \vec{b} b垂直,则 cos θ = 1 \cos\theta=1 cosθ=1则
a ⃗ ⋅ b ⃗ = ∣ a ⃗ ∣ ∣ b ⃗ ∣ cos θ = ∣ a ⃗ ∣ ∣ b ⃗ ∣ ( 2 ) \displaystyle\vec{a} \cdot \vec{b}=\left|\vec{a}\right|\left|\vec{b}\right|\cos\theta=\left|\vec{a}\right|\left|\vec{b}\right|\qquad\qquad\quad(2) a⋅b=∣a∣∣∣∣b∣∣∣cosθ=∣a∣∣∣∣b∣∣∣(2)
由(1)式可得
a ⃗ ⋅ b ⃗ = a 1 b 1 + a 2 b 2 ( 3 ) \vec{a} \cdot \vec{b}=a_{1}b_{1}+a_{2}b_{2}\qquad\qquad\qquad\qquad\qquad(3) a⋅b=a1b1+a2b2(3)
例1
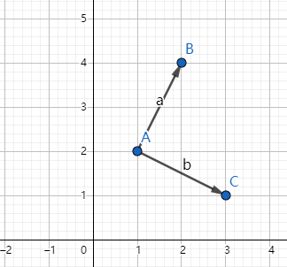
如图4所示,图中有两个向量 a ⃗ \vec{a} a与 b ⃗ \vec{b} b,A,B,C三点的坐标分别为A(1,2),B(2,4),C(3,1)。则
a ⃗ = ( a 1 , a 2 ) = ( 2 − 1 , 4 − 2 ) = ( 1 , 2 ) \vec{a}=(a_{1},a_{2})=(2-1,4-2)=(1,2) a=(a1,a2)=(2−1,4−2)=(1,2)
b ⃗ = ( b 1 , b 2 ) = ( 3 − 1 , 1 − 2 ) = ( 2 , − 1 ) \vec{b}=(b_{1},b_{2})=(3-1,1-2)=(2,-1) b=(b1,b2)=(3−1,1−2)=(2,−1)
所以
a ⃗ ⋅ b ⃗ = a 1 b 1 + a 2 b 2 = ( 1 × 2 + 2 × ( − 1 ) ) = 0 \vec{a} \cdot \vec{b}=a_{1}b_{1}+a_{2}b_{2}=(1×2+2×(-1))=0 a⋅b=a1b1+a2b2=(1×2+2×(−1))=0
因此,向量 a ⃗ \vec{a} a和 b ⃗ \vec{b} b正交,且两向量垂直。
规格化内积
a ⃗ ⋅ b ⃗ = 1 2 ( a 1 b 1 + a 2 b 2 ) \vec{a} \cdot \vec{b}=\frac12(a_{1}b_{1}+a_{2}b_{2}) a⋅b=21(a1b1+a2b2)
而规格化内积
a ⃗ ⋅ a ⃗ = 1 2 ( a 1 a 1 + a 2 a 2 ) = 1 2 ( 1 × 1 + 2 × 2 ) = 2.5 ≠ 1 \vec{a} \cdot \vec{a}=\frac12(a_{1}a_{1}+a_{2}a_{2})=\frac12(1×1+2×2)=2.5≠1 a⋅a=21(a1a1+a2a2)=21(1×1+2×2)=2.5=1
假设码片向量是2维的,这个2维的向量是不能作为发送站的码片向量的。
当两个m维向量有两个向量 a ⃗ = ( a 1 , a 2 , ⋯ a m ) \vec{a}=(a_{1},a_{2},{\cdots}a_{m}) a=(a1,a2,⋯am), b ⃗ = ( b 1 , b 2 , ⋯ b m ) \vec{b}=(b_{1},b_{2},{\cdots}b_{m}) b=(b1,b2,⋯bm),则规格化内积为
a ⃗ ⋅ b ⃗ = 1 m ∑ i = 0 m a i b i = 1 m ( a 1 b 1 + a 2 b 2 + ⋯ + a m b m ) ( 4 ) \vec{a} \cdot \vec{b}=\frac1m\displaystyle \sum^{m}_{i=0}{a_{i}b_{i}}=\frac1m(a_{1}b_{1}+a_{2}b_{2}+\cdots+a_{m}b_{m})\qquad\qquad\qquad(4) a⋅b=m1i=0∑maibi=m1(a1b1+a2b2+⋯+ambm)(4)
例2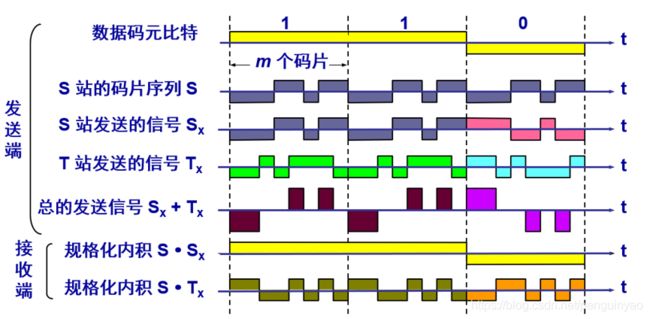
S站的码片序列S是(-1 -1 -1 +1 +1 -1 +1 +1)
T站的码片序列T是(-1 -1 +1 -1 +1 +1 +1 -1)
当数据码元比特为1时,发送信号 S x + T x S_{x}+T_{x} Sx+Tx是(-2 -2 0 0 2 0 2 0)
因为 S → ⋅ ( S x → + T x → ) = S → ⋅ S x → + S → ⋅ T x → \overrightarrow{S}\cdot (\overrightarrow{S_{x}}+\overrightarrow{T_{x}})=\overrightarrow{S}\cdot \overrightarrow{S_{x}}+\overrightarrow{S}\cdot \overrightarrow{T_{x}} S⋅(Sx+Tx)=S⋅Sx+S⋅Tx
且规格化内积
S → ⋅ S x → = 1 8 [ ( − 1 ) × ( − 1 ) + ( − 1 ) × ( − 1 ) + ( − 1 ) × ( − 1 ) + ( + 1 ) × ( + 1 ) + ( + 1 ) × ( + 1 ) + ( − 1 ) × ( − 1 ) + ( + 1 ) × ( + 1 ) + ( + 1 ) × ( + 1 ) ] = 1 \overrightarrow{S}\cdot \overrightarrow{S_{x}}=\frac{1}{8}[(-1)×(-1)+(-1)×(-1)+(-1)×(-1)+(+1)×(+1)+ (+1)×(+1)+(-1)×(-1)+(+1)×(+1)+(+1)×(+1)]=1 S⋅Sx=81[(−1)×(−1)+(−1)×(−1)+(−1)×(−1)+(+1)×(+1)+(+1)×(+1)+(−1)×(−1)+(+1)×(+1)+(+1)×(+1)]=1
规格化内积
S → ⋅ T x → = 1 8 [ ( − 1 ) × ( − 1 ) + ( − 1 ) × ( − 1 ) + ( − 1 ) × ( + 1 ) + ( + 1 ) × ( − 1 ) + ( + 1 ) × ( + 1 ) + ( − 1 ) × ( + 1 ) + ( + 1 ) × ( + 1 ) + ( + 1 ) × ( − 1 ) ] = 0 \overrightarrow{S}\cdot \overrightarrow{T_{x}}=\frac{1}{8}[(-1)×(-1)+(-1)×(-1)+(-1)×(+1)+(+1)×(-1)+(+1)×(+1)+(-1)×(+1)+(+1)×(+1)+(+1)×(-1)]=0 S⋅Tx=81[(−1)×(−1)+(−1)×(−1)+(−1)×(+1)+(+1)×(−1)+(+1)×(+1)+(−1)×(+1)+(+1)×(+1)+(+1)×(−1)]=0
所以
S → ⋅ ( S x → + T x → ) = S → ⋅ S x → + S → ⋅ T x → = 1 + 0 = 1 \overrightarrow{S}\cdot (\overrightarrow{S_{x}}+\overrightarrow{T_{x}})=\overrightarrow{S}\cdot \overrightarrow{S_{x}}+\overrightarrow{S}\cdot \overrightarrow{T_{x}}=1+0=1 S⋅(Sx+Tx)=S⋅Sx+S⋅Tx=1+0=1
所以S站发出的数据码元为1。
若计算的结果为-1,则说明S站发出的数据码元为0,若计算结果为0,则说明S站没有发送数据。