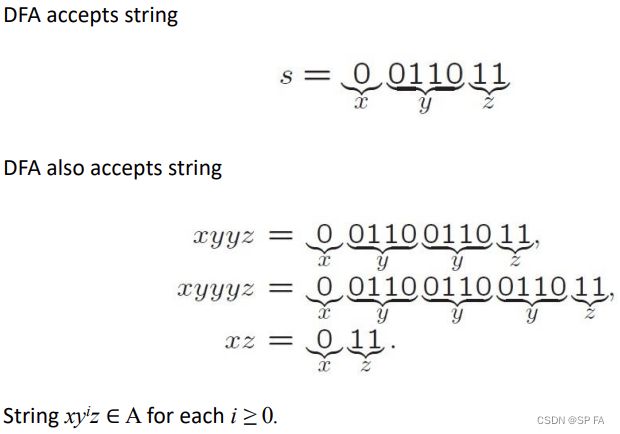INT201-Decision, Computation and Language

1. DFA

DFA is a finite-state machine that accepts or rejects a given string of symbols, by running through a state sequence uniquely determined by the string.

A DFA is defined as a 5-tuple:$$M=(Q,\Sigma ,\delta ,q,F)$$

1. $Q$ is a finite set of states.
2. $\Sigma$ is a finite set of symbols, called the alphabet of the automaton.
3. $\delta :Q\times \Sigma \to Q$ is a function, called the transition function.
4. $q\in Q$ is called the initial state.
5. $F\subseteq Q$ is a set of accepting / terminal states.

We can extend the definition of the transition function $\delta$ so that it tells us which state we reach after a word ${\Sigma }^{\ast }$ (not just a single letter) has been scanned:
extend the map $\delta :Q\times \Sigma \to Q$ to ${\delta }^{\ast }:Q\times {\Sigma }^{\ast }\to Q$ by defining:
$$\begin{array}{rl}{\delta }^{\ast }(q,ϵ)=q& \text{for all }q\in Q\\ {\delta }^{\ast }(q,wa)=\delta ({\delta }^{\ast }(q,w),a)& \text{for all }q\in Q,w\in {\Sigma }^{\ast },a\in \Sigma \\ {\delta }^{\ast }(q,vw)={\delta }^{\ast }({\delta }^{\ast }(q,v),w)& \text{for all }q\in Q,v,w\in {\Sigma }^{\ast }\end{array}$$

DFA 也可以看成是一张有向图

既然是一个图，那它也可以通过临接表的方式表示（可以试着画出下表的图）

1.1 Language defined by DFA

Suppose we have a DFA $M$, A word $w\in {\Sigma }^{\ast }$ is said to be accepted or recognized by $M$ if ${\delta }^{\ast }(q_0,w)\in F$, otherwise it is said to be rejected. The set of all words accepted by $M$ is called the language accepted by $M$ and will be denoted by $L(M)$.
$$L(M)=\{w\in {\Sigma }^{\ast }:{\delta }^{\ast }(q_0,w)\in F\}$$
Any finite language is accepted by some DFA

1.2 Regular operations on languages

A language $A$ is called regular, if there exists a finite automaton $M$ such that $A=L(M)$

Let $A$ and $B$ be two languages over the same alphabet.
The union of $A$ and $B$ is defined as:$$A\cup B=\{w:w\in A\text{ or }w\in B\}$$
The concatenation:$$AB=\{w{w}^{\prime }:w\in A\text{ and }{w}^{\prime }\in B\}$$
The Kleene star of $A$ is defined as:$$A^{\ast }=\bigcup _{i\in N}{A}_i=A_0\cup A_1\cup A_2\cdots$$where$$\begin{array}{rl}{A}_0& =\{ϵ\}\\ A_1& =A\\ A_{i+1}& =\{wv:w\in A_i,v\in A\}\end{array}$$

---

2. NFA

A finite automata is deterministic, if the next state the machine goes to on any given symbol is uniquely determined.

DFA has exactly one transition leaving each state for each symbol.

A finite automata is nondeterministic, if the machine allows for several or no choices to exist for the next state on a given symbol. For a state $q$ and symbol $s\in \Sigma$, NFA can have:

• Multiple edges leaving $q$ labelled with the same symbol $s$
• No edge leaving $q$ labelled with symbol $s$
• Edge leaving $q$ labelled with $ϵ$ (without reading any symbol)

The machine splits into multiple copies of itself (threads):

• Each copy proceeds with computation independently of others
• NFA may be in a set of states, instead of a single state.
• NFA follows all possible computation paths in parallel.
• If a copy is in a state and next input symbol doesn’t appear on any outgoing edge from the state, then the copy dies or crashes.
• NFA accepts the input string, if any copy ends in an accept state after reading the entire string.

For any alphabet $\Sigma$, we define ${\Sigma }_{ϵ}=\Sigma \cup \{ϵ\}$
NFA is a 5-tuple $M=(Q,\Sigma ,\delta ,q,F)$

1. $Q$ is a finite set of states
2. $\Sigma$ is a finite set of symbols, called the alphabet of the automaton
3. $\delta :Q\times {\Sigma }_{ϵ}\to P(Q)$ is a function, called the transition function
4. $q\in Q$ is called the initial / start state
5. $F\subseteq Q$ is a set of accepting / terminal states

Let $M=(Q,\Sigma ,\delta ,q,F)$ be an NFA, and let $w\in {\Sigma }^{\ast }$. We say that $M$ accepts $w$, if ${\delta }^{\ast }(q_0,w)\in F$

Extend the map $\delta$ to a map $Q\times {\Sigma }^{\ast }\to P(Q)$ by defining:$$\begin{array}{rl}\delta (q,ϵ)=\{q\}& \text{for all }q\in Q\\ \delta (q,wa)=\bigcup _{p\in \delta (q,w)}\delta (p,a)& \text{for all }q\in Q,w\in {\Sigma }^{\ast },a\in \Sigma \end{array}$$

Suppose, in a DFA, we can get from state $p$ to state $q$ via transitions labelled by letters of a word $w$. Then we say that the states $p$ and $q$ are connected by a path with label $w$.

In a NFA, if $\delta (p,a)=\{q,r\}$ we could write:$$\{p\}\stackrel{a}{⟶}\{q,r\}$$

2.1 Language accepted by NFA

Let $M=(Q,\Sigma ,\delta ,a,F)$ be an NFA. The language $L(M)$ accepted by $M$ is defined as$$L(M)=\{w\in {\Sigma }^{\ast }:M\text{ accepts }w\}$$

2.2 Equivalence of DFAs and NFAs

Two machines are equivalent if they recognize the same language.

DFA is a restricted form of NFA:

• Every NFA has an equivalent DFA
• We can convert an arbitrary NFA to a DFA that accepts the same language
• DFA has the same power as NFA

2.3 DFA to NFA

The formal conversion of a DFA to an NFA is done as follows: Let $M=(Q,\Sigma ,\delta ,q,F)$ be a DFA. $\delta$ is a function $\delta :Q\times \Sigma \to Q$. We define the function ${\delta }^{\prime }:Q\times {\Sigma }_{ϵ}\to P(Q)$. For any $r\in Q$ and for any $a\in {\Sigma }_{ϵ}$:$${\delta }^{\prime }(r,a)=\{\begin{array}{ll}\{\delta (r,a)\}& \text{if }a\ne ϵ\\ \varphi & \text{if }a=ϵ\end{array}$$Then $N=(Q,\Sigma ,{\delta }^{\prime })$ is an NFA, whose behavior is exactly the same as that of the DFA $M$, the easiest way to see this is by observing that the state diagrams of $M$ and $N$ are equal. Therefore, we have $L(M)=L(N)$

2.4 NFA to DFA

Definition 1
The $ϵ-\text{closure}$ of a set of states $R\subseteq Q$:
$$E(R)=\{q|q\text{ can be reached from }R\text{ by travelling over zero or more }ϵ\text{ transitions }\}$$

Definition 2
Suppose that there is a set of states $R$ and $a\in \Sigma$, we say that $R_a=ϵ-\text{closure}(J)$ where $J$ is the set that can be reached from $R$ by travelling over $a$

e.g.

通过以上两个定义得到下表：

R	$R_a$	$R_b$
{5,1}	{5,3,1}	{5,4,1}
{5,3,1}	{5,1,3,2,6,Y}	{5,4,1}
{5,4,1}	{5,3,1}	{5,1,4,2,6,Y}
{5,1,3,2,6,Y}	{5,1,3,2,6,Y}	{5,1,4,6,Y}
{5,1,4,2,6,Y}	{5,1,3,6,Y}	{5,1,4,2,6,Y}
{5,1,4,6,Y}	{5,1,3,6,Y}	{5,1,4,2,6,Y}
{5,1,3,6,Y}	{5,1,3,2,6,Y}	{5,1,4,6,Y}

然后进行重新编号：

S	a	b
0	1	2
1	3	2
2	1	4
3	3	5
4	6	4
5	6	4
6	3	5

这个表就是临接表，然后画图，就是 DFA

---

3. Regular Language

Definition

Previous: A language is regular if it is recognized by some DFA
Now: A language is regular if and only if some NFA recognizes it
Some operations on languages: Union, Concatenation and Kleene star

3.1 Closed under operation

A collection $S$ of objects is closed under operation $f$ if applying $f$ to members of $S$ always returns an object still in $S$.

Regular languages are indeed closed under the regular operations (Union, Concatenation, Kleene star)

3.1.1 Regular Languages Closed Under Union

Proof
$A$ and $B$ are regular languages over the same alphabet $\Sigma$, there are automata $M_1=(Q_1,\Sigma ,{\delta }_1,q_1,F_1)$ and $M_2=(Q_2,\Sigma ,{\delta }_2,q_2,F_2)$ that accept $A$ and $B$, respectively.

We can define $M=(Q,\Sigma ,\delta ,q,F)$ where:

• $Q=Q_1\times Q_2=\{(q_1,q_2):q_1\in Q_1\text{ and }{q}_2\in Q_2\}$
• $q=(q_1,q_2)$
• $F=\{(q_1,q_2):q_1\in F_1\text{ or }{q}_2\in F_2\}$
• $\delta :\delta ((q_1,q_2),a)=(\delta (q_1,a),\delta (q_2,a)),a\in \Sigma$

Then:$$M\text{ accept }w⟺{\delta }^{\ast }((q_1,q_2),w)\in F⟺{\delta }^{\ast }(q_1,w)\in F_1\text{ or }{\delta }^{\ast }(q_2,w)\in F_2$$

So that $L(M)=L(M_1)\cup L(M_2)$

Proof from the perspective of NFA
Consider $M_1,M_2$ are NFAs, we assume that $Q_1\cap Q_2=\varnothing$
We can define $M=(Q,\Sigma ,\delta ,q,F)$ where:

• $Q=\{q_0\}\cup Q_1\cup Q_2$
• $q_0$ is the start state of $M$
• $F=F_1\cup F_2$

Then:$$\delta (q,a)=\{\begin{array}{ll}{\delta }_1(q,a)& \text{if }r\in Q_1\\ {\delta }_2(q,a)& \text{if }r\in Q_2\\ \{q_1,q_2\}& \text{if }r=q_0\text{ and }a=ϵ\\ \varnothing & \text{if }r=q_0\text{ and }a\ne ϵ\end{array}$$

用图论的话来说，相当于建一虚点 $q_0$，指向两个 NFA 的起点。

3.1.2 Regular Languages Closed Under Concatenation

The concatenation of $A_1$ and $A_2$ is defined as:$$A_1{A}_2=\{w{w}^{\prime }:w\in A_1\text{ and }{w}^{\prime }\in A_2\}$$

Proof

• $Q=Q_1\cup Q_2$
• $q=q_1$
• $F=F_2$

Then:$$\delta (q,a)=\{\begin{array}{ll}{\delta }_1(q,a)& \text{if }q\in Q_1\text{ and }q\notin F_1\\ {\delta }_1(q,a)& \text{if }q\in F_1\text{ and }a\ne ϵ\\ {\delta }_1(q,a)\cup \{q_2\}& \text{if }q\in F_1\text{ and }a=ϵ\\ {\delta }_2(q,a)& \text{if }r\in Q_2\end{array}$$

相当于是把所有的 $F_1$ 连到了 $q_2$，有种首尾相接的感觉。

3.1.3 Regular Languages Closed Under Kleene star

Proof

• $Q=\{q_0\}\cup Q_1$
• $q_0$ is the start state of $M$
• $F=\{q_0\}\cup F_1$

Then:$$\delta (q,a)=\{\begin{array}{ll}{\delta }_1(q,a)& \text{if }q\in Q_1\text{ and }q\notin F_1\\ {\delta }_1(q,a)& \text{if }q\in F_1\text{ and }a\ne ϵ\\ {\delta }_1(q,a)\cup \{q_1\}& \text{if }q\in F_1\text{ and }a=ϵ\\ \{q_1\}& \text{if }q=q_0\text{ and }a=ϵ\\ \varnothing & \text{if }q=q_0\text{ and }a\ne ϵ\end{array}$$

所有 $F$ 都连到了 $q_1$ 上，白了就是递归

3.1.4 Regular Languages Closed Under Complement and Interaction

If $A$ is a regular language over the alphabet $\Sigma$, then the complement:$$\bar{A}\{w\in {\Sigma }^{\ast }:w\notin A\}$$is also a regular language.

If $A_1$ and $A_2$ are regular languages over the same alphabet $\Sigma$, then the interaction:$$A_1\cap A_2=\{w\in {\Sigma }^{\ast }:w\in A_1\text{ and }w\in A_2\}$$ is also a regular language.

3.2 Regular Expressions

Regular expressions are means to describe certain languages.

Let $\Sigma$ be a non-empty alphabet.

1. $ϵ$ is a regular expression
2. $\varnothing$ is a regular expression
3. For each $a\in \Sigma$, $a$ is a regular expression
4. If $R_1$ and $R_2$ are regular expressions, then $R_1\cup R_2$ is a regular expression, the same as $R_1{R}_2$, $R_1^{\ast }$

If $R$ is a regular expression, then $L(R)$ is the language generated / described / defined by $R$.
5. $ϵ$ describes the language $\{ϵ\}$
6. $\varnothing$ describes the language $\varnothing$
7. For each $a\in \Sigma$, the regular expression a describes the language $\{a\}$
8. If $R_1,R_2$ are regular expressions and $L_1,L_2$ are the languages described by them, respectively. $R_1\cup R_2$ describes the language $L_1\cup L_2$, the same as $R_1{R}_2$, $R_1^{\ast }$

3.3 Kleene’s Theorem

Let $L$ be a language. Then $L$ is regular iff there exists a regular expression that describes $L$.

• If a language is described by a regular expression, then it is regular.
• If a language is regular, then it has a regular expression.

3.4 GNFA

A GNFA can be defined as a 5-tuple $(Q,\Sigma ,\delta ,\{s\},\{t\})$

• $Q$ is a finite set of states
• $\Sigma$ is a finite set of alphabet
• $\delta :(Q\setminus \{t\})\times (Q\setminus \{s\})\to R$
• $s\in Q$
• $t\in Q$

3.4.1 DFA 转 GNFA

Convert a DFA into a regular expression

DFA转GNFA

3.5 Pumping Lemma for Regular Languages

A tool that can be used to prove that certain languages are not regular. This theorem states that all regular languages have a special property.

This property states that all strings in the language can be “pumped” if they are at least as long as a certain special value, called the pumping length. That means each such string contains a section that can be repeated any number of times with resulting string remaining in the language.

• If a language $L$ is regular, it always satisfies pumping lemma. If there exists at least one string made from pumping which is not in $L$, then $L$ is surely not regular.
• If pumping lemma holds, it does not mean that the language is regular.

e.g.

---

4. Context-Free Languages

4.1 CFG

Context-Free Grammar

A context-free grammar is a 4-tuple $G=(V,\Sigma ,R,S)$, where

• $V$ is a finite set, whose elements are called variables
• $\Sigma$ is a finite set, whose elements are called terminals
• $V\cap \Sigma =\varnothing$
• $S$ is an element of $V$, it is called the start variable
• $R$ is a finite set, whose elements are called rules. Each rule has the form $A\to w$, where $A\in V$ and $w\in (V\cup \Sigma {)}^{\ast }$

Definition 1: yeild $\Rightarrow$
Let $G=(V,\Sigma ,R,S)$ be a context free grammar with

• $A\in V$
• $u,v,w\in (V\cup \Sigma {)}^{\ast }$
• $A\to w$ is a rule of the grammar

The string $uwv$ can be derived in one step from the string $uAv$, written as$$uAv\Rightarrow uwv$$

Definition 2: derive $\stackrel{\ast }{\Rightarrow }$
Let $G=(V,\Sigma ,R,S)$ be a context free grammar with

• $u,v\in (V\cup \Sigma {)}^{\ast }$

The string $v$ can be derived from the string $u$, written as $u\stackrel{\ast }{\Rightarrow }v$, if one of the following conditions holds:

• $u=v$
• there exist an integer $k\ge 2$ and a sequence $u_1,u_2,\cdots ,u_k$ of strings in $(V\cup \Sigma {)}^{\ast }$, such that
  • $u=u_1$
  • $v=u_k$ and $u_1\Rightarrow u_2\Rightarrow u_3\cdots \Rightarrow u_k$

4.1.1 Language of CFG

The language of CFG $G=(V,\Sigma ,R,S)$ is$$L(G)=\{w\in {\Sigma }^{\ast }|S\stackrel{\ast }{\Rightarrow }w\}$$Such a language is called context-free, and satisfies $L(G)\subseteq {\Sigma }^{\ast }$

Theorem
Let $\Sigma$ be an alphabet and let $L\subseteq {\Sigma }^{\ast }$ be a regular language. Then $L$ is a context-free language (Every regular language is context-free)

Proof
Since $L$ is a regular language, there exists a deterministic finite automton $M=(Q,\Sigma ,\delta ,q,F)$ that accepts $L$. To prove that $L$ is context-free, we have to define a context-free grammar $G=(V,\Sigma ,R,S)$, such that $L=L(M)=L(G)$. Thus, $G$ must have the following property:

• For every string $w\in {\Sigma }^{\ast }$$$w\in L(M)\text{iff}w\in L(G)$$
• which can be reformulated as $$M\text{ accepts }w\text{ iff }S\stackrel{\ast }{\Rightarrow }w$$

Set $V=\{R_i|q_i\in Q\}$ that is, $G$ has a variable for every state of $M$. Now, for every transition $\delta (q_i,a)=q_j$ add a rule $R_i\to a{R}_j$. For every accepting state $q_i\in F$ add a rule $R_i\to ϵ$. Finally, make the start variable $S=R_0$

4.2 CNF

Chomsky Normal Form

A context-free grammar $G=(V,\Sigma ,R,S)$ is said to be in Chomsky normal form, if every rule in $R$ has one of the following three forms:

• $A\to BC$, where $A,B,C$ are elements of $V$, $B\ne S$ and $C\ne S$
• $A\to a$, where $A$ is an element of $V$ and $a$ is an element of $\Sigma$
• $S\to ϵ$, where $S$ is the start variable

Grammars in CNF are far easier to analyze.

Theorem
Let $\Sigma$ be an alphabet and let $L\subseteq {\Sigma }^{\ast }$ be a context-free language. There exists a context-free grammar in CNF, whose language is $L$. That is, every CFL can be described by a CFG in CNF

Proof
Given CFG $G=(V,\Sigma ,R,S)$. Replace, one-by-one, every rule that is not “Chomsky”

• Start variable (not allowed on RHS of rules)
• $ϵ$-rules ($A\to ϵ$ not allowed when $A$ isn’t start variable)
• all other violating rules ($A\to B,A\to aBc,A\to BCDE$)

4.2.1 Converting CFG into CNF

1. Eliminate the start variable from the right-hand side of the rules.
   • New start variable $S_0$
   • New rule $S_0\to S$
2. Remove $ϵ$-rules $A\to ϵ$, where $A\in V-\{S\}$. When removing $A\to ϵ$ rules, insert all new replacements
   • Before: $B\to AbA$ and $A\to ϵ|\cdots$
   • After: $B\to AbA|bA|Ab|b$ and $A\to \cdots$
3. Remove unit rules $A\to B$, where $A\in V$
   • Before: $A\to B$ and $B\to xCy$
   • After: $A\to xCy$ and $B\to xCy$
4. Eliminate all rules having more than two symbols on the right-hand side.
   • Before: $A\to B_1{B}_2{B}_3$
   • After: $A\to B_1{A}_1,A_1\to B_2{B}_3$
5. Eliminate all rules of the form $A\to ab$, where $a$ and $b$ are not both variables.
   • Before: $A\to ab$
   • After: $A\to B_1{B}_2,B_1\to a,B_2\to b$

4.3 PDA

Pushdown Automata
The class of languages that can be accepted by pushdown automata is exactly the class of context-free languages (finite automata are for regular languages).

• The input for a pushdown automaton is a string $w$ in ${\Sigma }^{\ast }$
• Different from finite automata, PDAs have a single stack.
• Stack have 2 different operations:
  • push: adds item to top of stack
  • pop: removes item from top of stack

• Tape: divided into cells that store symbols belonging to ${\Sigma }_{ϵ}=\Sigma \cup \{ϵ\}$
• Tape head: move along the tape, one cell to the right per move.
• Stack: containing symbols from a finite set $\Gamma$, called the stack alphabet. This set contains a special symbol $ (often mark bottom of stack).
• State control: can be in any one of a finite number of states. The set of states is denoted by $Q$. The set $Q$ contains one special state q, called the start state.

PDA Transition
If PDA

• in state $q_i$
• reads $a\in {\Sigma }_{ϵ}$
• pops $b\in {\Gamma }_{ϵ}$ off the stack

If $a=ϵ$, then no input symbol is read.
If $b=ϵ$, then nothing is popped off stack.

Then PDA

• moves to state $q_j$
• push $c\in {\Gamma }_{ϵ}$ onto top of stack

If $c=ϵ$, then nothing is pushed onto stack
If $c=u_1{u}_2\cdots u_k$ with $k\ge 1$ and $u_1,u_2,\cdots ,u_k\in \Gamma$, then $b$ is replaced by $c$, and $u_k$ becomes the new top symbol of the stack.

A pushdown automaton is a 6-tuple $M=(Q,\Sigma ,\Gamma ,\delta ,q,F)$

• $Q$ is finite set of states
• $\Sigma$ is (finite) input (tape) alphabet
• $\Gamma$ is (finite) stack alphabet
• $\delta$ is the transition function: $Q\times {\Sigma }_{ϵ}\times \Gamma \to Q\times \{N,R\}\times {\Gamma }_{ϵ}^{\ast }$
• $q\in Q$ is start state
• $F\subseteq Q$ is set of accept states

Let $r^{\prime }\in Q,\sigma \in \{N,R\}$, and $w\in {\Gamma }^{\ast }$ $$\delta (r,a,b)=(r^{\prime },\sigma ,c)$$

The tape head moves according to $\sigma$:

• If $\sigma =R$, it moves one cell to the right
• If $\sigma =N$, it does not move

4.3.1 Nondeterministic PDA

PDA transition function allows for nondeterminism $$\delta :Q\times {\Sigma }_{ϵ}\times {\Gamma }_{ϵ}\to P(Q\times {\Gamma }_{ϵ})$$

4.3.2 Language accepted by PDA

The set of all input strings that are accepted by PDA $M$ is the language recognized by $M$ and is denoted by $L(M)$

4.4 Equivalence of PDA and context-free languages

Let $\Sigma$ be an alphabet and let $A\subseteq {\Sigma }^{\ast }$ be a language. Then $A$ is context-free if and only if there exists a pushdown automaton that accepts $A$.

• If $A=L(G)$ for some CFG $G$, then $A=L(M)$ for some PDA $M$.
• If $A=L(M)$ for some PDA $M$, then $A=L(G)$ for some CFG $G$.

Proof: If $A=L(G)$ for some CFG $G$, then $A=L(M)$ for some PDA $M$.

Basic idea: Given CFG $G$, convert it into PDA $M$ with $L(M)=L(G)$ by building PDA that simulates a leftmost derivation.

However, PDA cannot push strings instead of $\le 1$ symbols onto stack. How can we solve this problem?$$\delta :Q\times {\Sigma }_{ϵ}\times {\Gamma }_{ϵ}\to P(Q\times {\Gamma }_{ϵ})$$

4.4.1 CFLs and regular languages

If $A$ is a regular language, then $A$ is also a CFL.

Proof

• Suppose $A$ is regular, so it has a corresponding NFA
• NFA is a PDA without stack.
• So $A$ has a PDA
• $A$ is context-free

4.5 The pumping lemma for context-free languages

4.5.1 Pumping Lemma for CFLs

Let $L$ be a context-free language. Then there exists an integer $p\ge 1$, called the pumping length, such that the following holds: Every string s in $L$, with $|s|\ge p$, can be written as $s=uvxyz$, such that

• $|vy|\ge 1$
• $|vxy|\le p$
• $u{v}^{i}x{y}^{i}z\in L$, for all $i\ge 0$.

Split String Using Parse Tree

• More generally, consider “long” string $s\in A$.
• Parse tree is “tall”, $\exists$ repeated variable $R$ in path from root $S$ to leaf.
• Split string $s=uvxyz$ into 5 pieces based on repeated variable $R$:
  • $u$ is before $R-R$ subtree (in depth-first order)
  • $v$ is before second $R$ subtree within $R-R$ subtree
  • $x$ is what second $R$ eventually becomes
  • $y$ is after second $R$ within $R-R$ subtree
  • $z$ is after $R-R$ subtree

---

5. Turing Machine

• $k\ge 1$ infinitely long tape (The tape is infinite both to the left and to the right), divided into cells. Each cell stores a symbol belonging to $\Gamma$ (tape alphabet).
• Tape head can move both right and left, one cell per move. It read from or write to a tape.
• State control can be in any one of a finite number of states $Q$. It is based on: state and symbol read from tape.
• Machine has one start state, one accept state and one reject state.
• Machine can run forever: infinite loop.

Properties of Turing Machine

• Turing machine can both read from tape and write on it.
• Tape head can move both right and left.
• Tape is infinite and can be used for storage.
• Accept and reject states take immediate effect.

A Turing machine ™ is a 7-tuple $M=(\Sigma ,\Gamma ,Q,\delta ,q,q_{accept},q_{reject})$, where

• $\Sigma$ is a finite set, called the input alphabet; the blank symbol is not contained in $\Sigma$
• $\Gamma$ is a finite set, called the tape alphabet; this alphabet contains the blank symbol, and $\Sigma \subseteq \Gamma$
• $Q$ is a finite set, whose elements are called states
• $q$ is an element of $Q$; it is called the start state
• $q_{accept}$ is an element of $Q$; it is called the accept state
• $q_{reject}$ is an element of $Q$; it is called the reject state, $q_{reject}\ne q_{accept}$
• $\delta$ is called the transition function, which is a function $\delta :Q\times \Gamma \to Q\times \Gamma \times \{L,R,N\}$
  $L$: move to left, $R$: move to right, $N$: no move.

Transition function

$\delta (q,a)=(s,b,L)$

If TM

• in state $q\in Q$
• tape head reads tape symbol $a\in \Gamma$

Then TM

• moves to state $s\in Q$
• overwrites $a$ with $b\in \Gamma$
• moves head left

Computation steps

• Before the computation step, the Turing machine is in a state KaTeX parse error: Undefined control sequence: \inQ at position 2: r\̲i̲n̲Q̲, and the tape head is on a certain cell.
• TM $M$ proceeds according to transition function:$$\delta :Q\times \Gamma \to Q\times \Gamma \times \{L,R,N\}$$
• Depending on $r$ and $k$ symbols read from tape:
  • switches to a state $r^{\prime }\in Q$
  • tape head writes a symbol of $\Gamma$ in the cell it is currently scanning
  • tape head moves one cell to the left or right or stay at the current cell.
• Computation continues until $q_{reject}$ or $q_{accept}$ is entered.
• Otherwise, $M$ will run forever (input string is neither accepted nor rejected)

Start configuration
The input is a string over the input alphabet $\Sigma$. Initially, this input string is stored on the first tape, and the head of this tape is on the leftmost symbol of the input string.

Computation and termination
Starting in the start configuration, the Turing machine performs a sequence of computation steps. The computation terminates at the moment when the Turing machine enters the accept state $q_{accept}$ or the reject state $q_{reject}$. (If the machine never enters $q_{accept}$ and $q_{reject}$ the computation does not terminate.)

Acceptance
The Turing machine $M$ accepts the input string $w\in {\Sigma }^{\ast }$ , if the computation on this input terminates in the state $q_{accept}$.

5.1 TM Configuration

Configuration of a TM $M=(Q,\Sigma ,\Gamma ,\delta ,q,q_{accept},q_{reject})$ is a string $uqv$ with $u,v\in {\Gamma }^{\ast }$ and $q\in Q$, and specifies that currently

• $M$ is in state $q$
• tape contains $uv$
• tape head is pointing to the cell containing the first symbol in $v$

5.2 TM Transitions

Configuration $C1$ yields configuration $C2$ if the Turing machine can legally go from $C1$ to $C2$ in a single step. For TM $M=(Q,\Sigma ,\Gamma ,\delta ,q,q_{accept},q_{reject})$, suppose

• $u,v\in {\Gamma }^{\ast }$
• $a,b,c\in \Gamma$
• $q_i,q_j\in Q$
• transition function $\delta :Q\times \Gamma \to Q\times \Gamma \times \{L,R\}$

5.3 TM Computation

Given a TM $M=(Q,\Sigma ,\Gamma ,\delta ,q,q_{accept},q_{reject})$ and input string $w\in {\Sigma }^{\ast }$. $M$ accepts input $w$ if there is a finite sequence of configurations $C_1,C_2,\dots ,C_k$ for some $k\ge 1$ with

• $C_1$ is the starting configuration $q0w$
• $C_i$ yields $C_{i+1}$ for all $i=1,\dots ,k-1$ ((sequence of configurations obeys transition function $\delta$)
• $C_k$ is an accepting configuration $u{q}_{accept}v$ for some $u,v\in {\Gamma }^{\ast }$

5.4 Language accepted by TM

The language $L(M)$ accepted by the Turing machine $M$ is the set of all strings in ${\Sigma }^{\ast }$ that are accepted by $M$.

Language $A$ is Turing-recognizable if there is a TM $M$ such that $A=L(M)$

• Also called recursively enumerable or enumerable language.
• On an input $w\in L(M)$, the machine $M$ can either halt in a rejecting state, or it can loop indefinitely.
• Turing-recognizable not practical because never know if TM will halt.

5.5 Decider

A decider is TM that halts on all inputs

Language $A=L(M)$ is decided by TM $M$ if on each possible input $w\in {\Sigma }^{\ast }$, the TM finishes in a halting configuration

• $M$ ends in $q_{accept}$ for each $w\in A$
• $M$ ends in $q_{reject}$ for each $w\in A$

$A$ is Turing-decidable if $\exists$ TM $M$ that decides A

• Also called recursive or decidable language.
• Differences to Turing-recognizable language:
  • Turing-decidable language has TM that halts on every string $w\in {\Sigma }^{\ast }$
  • TM for Turing-recognizable language may loop on strings $w\notin$ this language

5.6 Multi-tape TM

• Each tape has its own head
• Transition determined by
  • state
  • the content read by all heads
• Reading and writing of each head are independent of others

A k-tape Turing machine ™ is a 7-tuple $M=(\Sigma ,\Gamma ,Q,\delta ,q,q_{accept},q_{reject})$ has $k$ different tapes and $k$ different read/write heads, where,

• $\Sigma$ is a finite set, called the input alphabet; the blank symbol $ϵ$ is not contained in $\Sigma$.
• $\Gamma$ is a finite set, called the tape alphabet; this alphabet contains the blank symbol $ϵ$, and $\Sigma \subseteq \Gamma$
• $Q$ is a finite set, whose elements are called states
• $q$ is an element of $Q$; it is called the start state
• $q_{accept}$ is an element of $Q$; it is called the accept state
• $q_{reject}$ is an element of $Q$; it is called the reject state
• $\delta$ is called the transition function, which is a function $\delta :Q\times {\Gamma }^k\to Q\times {\Gamma }^k\times \{L,R,N{\}}^k$
  ${\Gamma }^k=\Gamma \times \Gamma \times \cdots \times \Gamma$

Transition function
$$\delta :Q\times {\Gamma }^k\to Q\times {\Gamma }^k\times \{L,R,N{\}}^k$$
Given $\delta (q_i,a_1,a_2,\cdots ,a_k)=(q_j,b_1,b_2,\cdots ,b_k,L,R,\cdots ,L)$

5.6.1 Multi-tape TM equivalent to 1-tape TM

simulate k-tape TM using 1-tape TM

Proof
Let TM $M=(\Sigma ,\Gamma ,Q,\delta ,q,q_{accept},q_{reject})$ be a k-tape TM.

$M$ has:

• input $w=w_1,w_2,\cdots ,w_k$
• other tapes contain only blanks $ϵ$
• each head points to first cell.

Construct 1-tape TM $M^{\prime }$ by extending tape alphabet $${\Gamma }^{\prime }=\Gamma \cup \dot{\Gamma }\cup \{\#\}$$where $\dot{\Gamma }$ contains the head positions of different tapes. These positions are marked by dotted symbol.

For each step of k-tape TM $M$, 1-tape $M^{\prime }$ operates its tape as:

• At the start of the simulation, the tape head of $M^{\prime }$ is on the leftmost $\#$
• Scans the tape from first $\#$ to $(k+1)st\#$ to read symbols under heads.
• Rescans to write new symbol and move heads.

Turing recognizable & Multiple-tape TM
Language $L$ is TM-recognizable if and only if some multi-tape TM recognizes $L$.

5.7 Nondeterministic TM

A nondeterministic Turing machine (NTM) M can have several options at every step. It is defined by the 7-tuple $M=(\Sigma ,\Gamma ,Q,\delta ,q,q_{accept},q_{reject})$, where

• $\Sigma$ is input alphabet (withoutblank)
• $\Gamma$ is tape alphabet with $\{ϵ\}\cup \Sigma \subseteq \Gamma$
• $Q$ is a finite set, whose elements are called states
• $\delta$ is transition function $\delta :Q\times \Gamma \to P(Q\times \Gamma \times \{L,R\})$
• $q$ is start state $\in Q$
• $q_{accept}$ is accept state $\in Q$
• $q_{reject}$ is reject state $\in Q$

Transition

Computation
With any input $w$, computation of NTM is represented by a configuration tree.

If $\exists$ at least one accepting leaf, then NTM accepts.

5.7.1 Address

Every node in the tree has at most $b$ children. $b$ is size of largest set of possible choices for $N^{\prime }s$ transition function.

• Every node in tree has an address that is a string over the alphabet ${\Gamma }_b=\{1,2,\cdots ,b\}$

5.7.2 NTM equivalent to TM

Every nondeterministic TM has an equivalent deterministic TM.

Proof

• Build TM $D$ to simulate NTM $N$ on each input $w$. $D$ tries all possible branches of $N^{\prime }s$ tree of configurations.
• If $D$ finds any accepting configuration, then it accepts input $w$.
• If all branches reject, then $D$ rejects input $w$.
• If no branch accepts and at least one loops, then $D$ loops on $w$.

1. Initially, input tape contains input string $w$. Simulation and address tapes are initially empty.
2. Copy input tape to simulation tape.
3. Use simulation tape to simulate NTM $N$ on input $w$ on path in tree from root to the address on address tape.
   • At each node, consult next symbol on address tape to determine which branch to take.
   • Accept if accepting configuration reached.
   • Skip to next step if
     • symbols on address tape exhausted.
     • nondeterministic choice invalid
     • rejecting configuration reached
4. Replace string on address tape with next string in ${\Gamma }_b^{\ast }$ in string order, and go to Stage 2.

Turing recognizable & Multiple-tape TM
Language L is TM-recognizable if a NTM recognizes it. Multiple-tape TMs and NTMs are not more powerful than standard TMs.

Turing decidable & NTM decidable
A nondeterministic TM is a decider if all branches halt on all inputs. A language is decidable if some nondeterministic TM decides it.

5.8 Enumerable Language and Enumerator

A language is enumerable if some TM recognizes it.

An enumerator is usually represented as a 2-tape Turing machine. One working tape, and one print tape.

Language A is Turing-recognizable if some enumerator enumerates it.

5.9 Encoding

Input to a Turing machine is a string of symbols over an alphabet

When we want TMs to work on different objects, we need to encode this object as a string of symbols over an alphabet.

5.9.1 Encoding of Graph

Given an undirected graph $G$

$<G>$ of graph $G$ is string of symbols over some alphabet $\Sigma$, where the string starts with list of nodes and followed by list of edges.

5.9.2 TM to decide the connectedness of a Graph

An undirected graph is connected if every node can be reached from any other node by travelling along edge. Let $A$ be the language consisting of strings representing connected undirected graph.

On input $<G>\in \Omega$, where $G$ is an undirected graph

• Check if $G$ is a valid graph encoding. If not, reject.
• Select first node of $G$ and mark it.
• Repeat until no new nodes marked.
• For each node in $G$, mark it if it’s attached by an edge to a node already marked.
• Scan all nodes of $G$ to see whether they all are marked. If they are, accept; otherwise, reject.

$\Omega$ denotes the universe of a decision problem, comprising all instances.

For TM $M$ that decides $$A=\{<G>|G\text{ is a connected undirected graph}\}$$ $$D=\{<G>|G\text{ is an undirected graph}\}$$

Step 1 checks that input $G\in \Omega$ is valid encoding:

• Two list
  • First is a list of numbers
  • Second is a list of pairs of numbers
• First list contains no duplicate
• Every node in second list appears in first list

Step 2-5 check if $G$ is connected.