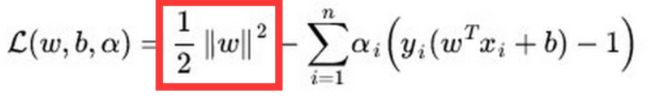机器学习 - - - LR和SVM的联系与区别?
解析一
LR和SVM都可以处理分类问题,且一般都用于处理线性二分类问题(在改进的情况下可以处理多分类问题)
区别:
1、LR是参数模型,svm是非参数模型,linear和rbf则是针对数据线性可分和不可分的区别;
2、从目标函数来看,区别在于逻辑回归采用的是logistical loss,SVM采用的是hinge loss,这两个损失函数的目的都是增加对分类影响较大的数据点的权重,减少与分类关系较小的数据点的权重。
3、SVM的处理方法是只考虑support vectors,也就是和分类最相关的少数点,去学习分类器。而逻辑回归通过非线性映射,大大减小了离分类平面较远的点的权重,相对提升了与分类最相关的数据点的权重。
4、逻辑回归相对来说模型更简单,好理解,特别是大规模线性分类时比较方便。而SVM的理解和优化相对来说复杂一些,SVM转化为对偶问题后,分类只需要计算与少数几个支持向量的距离,这个在进行复杂核函数计算时优势很明显,能够大大简化模型和计算。
5、logic 能做的 svm能做,但可能在准确率上有问题,svm能做的logic有的做不了。
解析二
相同点
①都是线性分类器。本质上都是求一个最佳分类超平面。
②都是监督学习算法。
③都是判别模型。判别模型不关心数据是怎么生成的,它只关心信号之间的差别,然后用差别来简单对给定的一个信号进行分类。常见的判别模型有:KNN、SVM、LR,常见的生成模型有:朴素贝叶斯,隐马尔可夫模型。
不同点
1) 本质上是损失函数不同
LR的损失函数是交叉熵:
SVM的目标函数:
逻辑回归基于概率理论,假设样本为正样本的概率可以用sigmoid函数(S型函数)来表示,然后通过极大似然估计的方法估计出参数的值。
支持向量机基于几何间隔最大化原理,认为存在最大几何间隔的分类面为最优分类面。
2) 两个模型对数据和参数的敏感程度不同
SVM考虑分类边界线附近的样本(决定分类超平面的样本)。在支持向量外添加或减少任何样本点对分类决策面没有任何影响;
LR受所有数据点的影响。直接依赖数据分布,每个样本点都会影响决策面的结果。如果训练数据不同类别严重不平衡,则一般需要先对数据做平衡处理,让不同类别的样本尽量平衡。
3) SVM 基于距离分类,LR 基于概率分类。
SVM依赖数据表达的距离测度,所以需要对数据先做 normalization;LR不受其影响。
4) 在解决非线性问题时,支持向量机采用核函数的机制,而LR通常不采用核函数的方法。
SVM算法里,只有少数几个代表支持向量的样本参与分类决策计算,也就是只有少数几个样本需要参与核函数的计算。
LR算法里,每个样本点都必须参与分类决策的计算过程,也就是说,假设我们在LR里也运用核函数的原理,那么每个样本点都必须参与核计算,这带来的计算复杂度是相当高的。尤其是数据量很大时,我们无法承受。所以,在具体应用时,LR很少运用核函数机制。
5) 在小规模数据集上,Linear SVM要略好于LR,但差别也不是特别大,而且Linear SVM的计算复杂度受数据量限制,对海量数据LR使用更加广泛。
6) SVM的损失函数就自带正则,而 LR 必须另外在损失函数之外添加正则项。
红框内就是L2正则。
看到有对参数模型和非参数模型不理解的,这里进行补充:
非参数模型(non-parametric model)和参数模型(parametric model)作为数理统计学中的概念,现在也常用于机器学习领域中。
在统计学中,参数模型通常假设总体服从某个分布,这个分布可以由一些参数确定,如正态分布由均值和标准差确定,在此基础上构建的模型称为参数模型;非参数模型对于总体的分布不做任何假设或者说是数据分布假设自由,只知道其分布是存在的,所以就无法得到其分布的相关参数,只能通过非参数统计的方法进行推断。
所以说,参数模型和非参数模型中的“参数”并不是模型中的参数,而是数据分布的参数。
看了各种解答之后,我觉得二者可以这样进行区分:
一、首先需要明确的是 非参数模型并不是说模型中没有参数!
这里的non-parametric类似单词priceless,并不是没有价值,而是价值非常高,无价,也就是参数是非常非常非常多的!(注意:所谓“多”的标准,就是参数数目大体和样本规模差不多)
而:可以通过有限个参数来确定一个模型,这样的方式就是“有参数模型”,也就是这里说的参数模型,如线性回归、Logistic回归(假定样本维度为N,则假定N个参数theta1,theta2...thetaN)。
二、其次:参数模型 :对学到的函数方程有特定的形式,也就是明确指定了目标函数的形式 -- 比如线性回归模型,就是一次方程的形式,然后通过训练数据学习到具体的参数。
所以参数机器学习模型包括两个部分:
1、选择合适的目标函数的形式。
2、通过训练数据学习目标函数的参数。
通常来说,目标函数的形式假设是:对于输入变量的线性联合,于是参数机器学习算法通常被称为“线性机器学习算法”。
三、非参数机器学习算法:对于目标函数形式不作过多的假设的算法称为非参数机器学习算法。通过不做假设,算法可以自由的从训练数据中学习任意形式的函数。
对于理解非参数模型的一个好例子是k近邻算法,其目标是基于k个最相近的模式对新的数据做预测。这种理论对于目标函数的形式,除了相似模式的数目以外不作任何假设。
四、最后:
常见的参数机器学习模型有:
1、逻辑回归(logistic regression)
2、线性成分分析(linear regression)
3、感知机(perceptron)(假设分类超平面是wx+b=0)
参数机器学习算法有如下优点:
1、简洁:理论容易理解和解释结果。
2、快速:参数模型学习和训练的速度都很快。
3、数据更少:通常不需要大量的数据,在对数据的拟合不很好时表现也不错。
参数机器学习算法的局限性:
1、拘束:以指定的函数形式来指定学习方式。
2、有限的复杂度:通常只能应对简单的问题。
3、拟合度小:实际中通常无法和潜在的目标函数完全吻合,也就是容易出现欠拟合。
常见的非参数机器学习模型有:
1、决策树
2、朴素贝叶斯
3、支持向量机(SVM的例子中,SVM的参数α数目和样本数目相同,从定义看来,因为参数数目和样本规模相当,所以属于无参数模型。当然,SVM通过得到支撑向量的方式,只有若干样本的参数α不为0,从这个角度,SVM还属于“稀疏模型”,这又属于另外一码事了。)
4、神经网络
非参数机器学习算法的优势有:
1、可变性:可以拟合许多不同的函数形式。
2、模型强大:对于目标函数不做假设或者作出很小的假设。
3、表现良好:对于训练样本数据具有良好的拟合性。
非参数机器学习算法的局限性:
1、需要更多数据:对于拟合目标函数需要更多的训练数据。
2、速度慢:因为需要训练跟多的参数,所以训练过程通常比较慢。
3、过拟合:有较高的风险发生过拟合,对于预测的效果解释性不高。
七月双十二活动已正式开启 · 40门AI好课1分起秒!
课程涵盖 ML | DL | CV | NLP | 推荐 全方向课程
活动时间:2021.12.07 - 12.14
仅限一周,活动主会场~ ▼▼▼http://www.julyedu.com![]() http://www.julyedu.com
http://www.julyedu.com