Heatmap Distribution Matching for Human Pose Estimation 阅读笔记

用于人体姿态估计的热图分布匹配

NeurIPS 2022
论文链接
其他参考链接
代码未开源

摘要： 大多工作将2D姿态估计视作热图估计任务，并使用 Gaussian-smoothed 热图作优化目标，使用 pixel-wise loss（例如MSE）来优化预测热图。本文表明：以这种方式优化预测热图可能不会优化模型定位身体关节的性能。 为解决此问题，本研究从一个新的角度将预测热图的优化阐述为：预测热图和身体关节的标注点间的分布匹配问题。我们提出的方法无需构造平滑高斯热图，可以在优化预测热图过程中改进模型性能。COCO和MPII数据集上的大量实验表明了本方法的有效性。

---

1 Introduction

2D人体姿态估计致力于定位人体关节点，与动作识别、人机交互、手语理解多种应用相关。最近一些工作将姿态估计视作热图估计任务，为每个关节估计一张 grid-like 热图，热图的每个像素值表示该像素包含身体关节的概率。相较于坐标回归法，热图法在整个编码解码过程中保持输入图像的空间结构，性能更稳定。
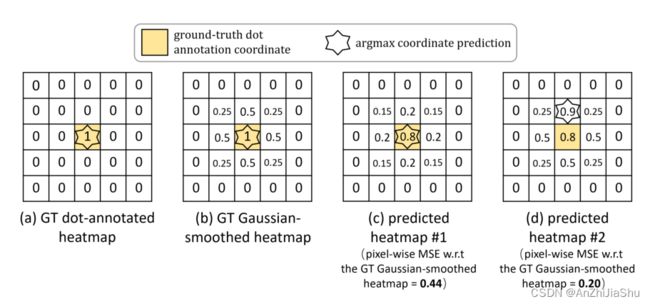
优化预测热图是热图法训练过程的关键，如图1(a)所示，通过为每个身体关节构建一张 dot-annotated 热图，然后逐像素比较预测热图和 dot-annotated 热图间的差异来优化预测热图。但dot-annotated 热图除表示身体关节的点像素外，其他像素都为0值，因此以该方式优化热图可能导致慢收敛和次优性能，可以通过构造平滑高斯热图来解决此问题，如图1(b)所示，对身体关节标注点进行平滑来构建平滑高斯热图。
但GT平滑高斯热图存在下列问题：

1. 首先，需要选择合适的标准差来构建高斯平滑热图，但实现最佳性能的标准差通常会因不同类型的身体关节、不同的身体姿态和不同的身体尺寸而不同，因此需要谨慎选择合适的标准差。
2. 通过逐像素做 MSE 来优化预测热图预测的过程中，可能并不能直接优化模型定位身体关节的性能（DSNT中提出的）。如图1所示，虽然 heatmap#1的MSE值> heatmap#2的MSE值，但显然heatmap#1预测的关节点更准确。

图1：热图图解。尽管 heatmap#1的MSE值> heatmap#2的MSE值，但显然heatmap#1预测的关节点更准确。

使用 dot-annotated 热图和 Gaussian-smoothed热图作GT热图都存在缺点。因此本文提出通过最小化预测热图和标注点之间的差异来直接优化预测热图，这样可以直接优化模型来精确定位身体关节点，而非间接优化dot-annotated 热图和 Gaussian-smoothed热图。但热图的像素数量与标注点的数量不同，因此不能简单的通过测量预测热图和标注点之间的条目差异来测量二者的差异。为解决该问题，通过测量两个分布的Earth Mover’s Distance来测量二者的差异，即使它们有不同数量的条目，因此本文将预测热图预测的优化阐述为分布匹配问题。具体而言，分别构建预测热图分布和标注点的分布，然后基于Earth Mover’s Distance来最小化二者的分布，从而优化预测热图。该方法直接通过标注点优化预测热图，既不需要构造平滑高斯热图，也避免了 binary dot-annotated 热图问题，可以实现优异性能。
我们提出的方法简单有效，将原始的2D姿态估计任务的loss替换成我们的loss来测量预测热图和标注点之间的分布差异，可以实现性能改进。本工作贡献如下：

1. 分析出在最小化预测热图和GT热图间逐像素的MSE过程中，可能不能直接优化人体姿态估计模型性能。
2. 从一个新角度出发，将预测热图的优化表述为预测热图和GT标注点之间的分布匹配问题，绕过了构建平滑高斯热图的步骤，直接改善模型性能。
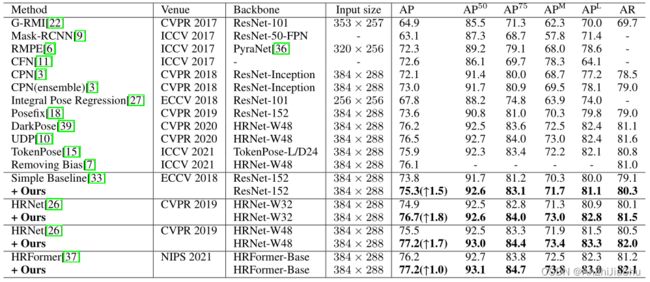
3. 我们提出的方法在评估基准上实现了sota。

2 Related Work

2D Human Pose Estimation. 2D人体姿态估计除了平滑高斯热图法之外，[Integral human pose regression，Removing the bias of integral pose regression，Dive deeper into integral pose regression] 结合热图与坐标回归思想，将预测热图的期望值作为预测坐标。我们的方法绕过回归步骤和构建平滑高斯热图作为优化目标的步骤，从一个新角度，通过最小化预测热图和标注点之间的分布差异，将优化预测热图阐述为分布匹配问题。

Distribution Matching. 分布匹配的思想已经应用于图像检索、跟踪、少样本学习、长尾识别（long-tail，指分类问题中数据集类别数不一致）等各种任务中。本研究设计了一种新的分布匹配方案，在2D人体姿态估计 sub-pixel 分辨率的帮助下优化热图预测。

3 Method

本研究将热图预测的优化阐述为分布匹配问题，基于 Earth Mover’s Distance 最小化预测热图分布与标注点分布间的差异，用标注的关节点直接优化预测热图。

3.1 Revisiting Earth Mover’s Distance

Earth Mover’s Distance 用于测量两种概率分布间的差异，可以理解为计算将mass 从一种分布 transport 到另一种分布所需的最佳成本。 为计算Earth Mover’s Distance ，将源分布视为一组(N个) suppliers：$S=(s_1,...,s_N{)}^T$，$s_n$ 表示 n-th supplier 所拥有的 total units of mass，将目标分布视为(M) 个 demanders：$D=(d_1,...,d_M{)}^T$ 的集合，$d_m$ 表示 m-th demander 所需要的 total units of mass。$C\in R_{\ge 0}^{N\times M}$ 是源分布与目标分布间的 cost function，$C_{n,m}$ 表示从n-th supplier 向 m-th demander 运输 a unit of mass 的 cost。我们的目标是从一系列将所有mass从N个suppliers运输到M个demanders的计划 $P＝\{P\in R_{\ge 0}^{N\times M}:p1=S\&p^{T}1=D\}$ 中选择一个 least-cost 运输计划，1表示一个ones vector。Earth Mover’s Distance：$E_C(s,D)$ 表示least-cost transportation plan 的 cost，其公式如下：

但直接优化等式1的计算复杂性高，为降低计算成本，特别是在处理大规模问题时，使用正则化 Earth Mover’s Distance公式：

3.2 Problem Formulation

下面通过构建supplier: S、demander: D和 cost function: C，将预测热图的优化表述为分布匹配问题。
The suppliers S. $H_{pred}\in R^{H\times W}$ 表示一个身体关节的预测热图，为了公式化 supplier S 来表示 $H_{pred}$，先定位 H×W 个 suppliers 来对应 $H_{pred}$ 中的H×W个像素；然后，为确定每个 supplier 存储的 mass units，且 suppliers 不能有 negative mass units，因此基于$H_{pred}$ 的一个 non-nagetive 公式构造S。此外，限制S存储的 total units of mass = D所需的 total units of mass。为了满足这些要求，先将 $H_{pred}$ 传给relu激活函数，然后将其归一化为：

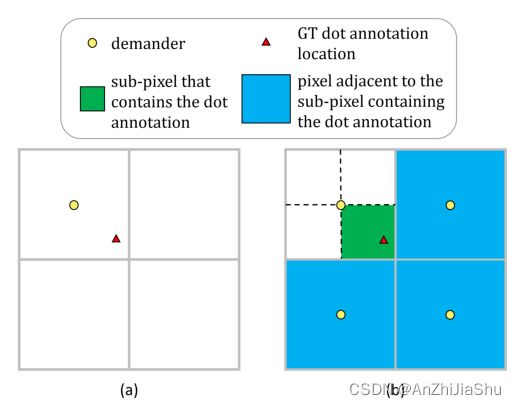
The demanders D. 对于demander，针对每个身体关节构造D，以表示其相应的GT标注点。对于每个关节，D的一个 naive formulation 是识别包含GT标注点的像素（即图2(a)中的左上像素），并在该像素的中心构建单个demander（即图2(a)中的黄点）。但以此种方式公式化的demander可能与GT标注点明显不同，因此可能导致次优模型性能。通常，输出热图的分辨率都低于输入图像，如图2(a) 所示，分辨率的差距使得 demander 和标注点位置之间存在不容忽视的距离，可能会影响姿态估计模型的性能。
我们的目标是克服分辨率的差距使demander的公式更准确的表示标注点，可以使用 sub-pixel 分辨率推理更准确的位置信息，因此用以下4步公式化D：

1. 如图2(b) 的左上角所示，先将包含标注点的像素拆分为4个“sub-pixel”（四个由虚线分隔的正方形）。
2. 之后，识别标注点所在的“sub-pixel”（即图2(b) 所示的绿色 sub-pixel）。
3. 然后，如图2(b) 中的四个黄色点所示，将一组4个 demanders 定位在包含所标识的“sub-pixel”的像素（即图2(b)中的左上像素）和与所标识 sub-pixel 相邻的三个像素（即，图2(a)中的三个蓝色像素）的中心。
4. 最后，通过以下方式确定每个 demander 所需的 units of mass，以便使用4个 demanders 精确表示标注点：g 表示两个相邻像素中心间的2D欧氏距离（也是像素大小），GT标注点的坐标表示为：$(x_{dot},y_{dot})$，i-th demander 的坐标表示为$(x_i,y_i)$, i∈ {1, 2, 3, 4}。然后将demanders D构造为：
   
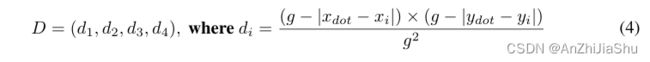
   di 表示 i-th demander 所需的 units of mass。以此方式设计 di 可以实现以下两个属性：(1) 给离标注点更近的 demander 分配更多mass，给离标注点更远的demander 分配更少mass，可以精确将标注点表示为： $(x_{dot},y_{dot})=(d_1\times x_1+d_2\times x_2+d_3\times x_3+d_4\times x_4,d_1\times y_1+d_2\times y_2+d_3\times y_3+d_4\times y_4)$，因此，无论热图分辨率比原图分辨率低多少，以这种方式构造的 demander D 都可以准确表示GT标注点。(2) 此外，由于 d1+d2+d3+d4＝1，demander D所需的 total units of mass也被约束为与 suppliers S所存储的 total units of mass相同。
   

图2：(a) demanders D的naive formulation; (b) 包含sub-pixel概念的demanders D 的公式。

The cost function C： 需要构造一个 cost function: $C\in R_{\ge 0}^{HW\times 4}$ 来通过计算根据预测热图构建的 H×W 个suppliers S 和 根据GT标注点构造的4个demander间的 Earth Mover’s Distance来测量二者的分布差异。$(x_{s_n},y_{s_n})$，n ∈ {1, …, H × W } 表示 n-th supplier 的坐标，$(x_{s_m},y_{s_m})$，m ∈ {1, 2, 3,4} 表示 m-th demander 的坐标，将从 n-th supplier 向 m-th demander 运输 per unit 的 cost：$C_{n,m}$ 定义为二者的 L2 距离，即：
使用这样的成本函数，可以通过最小化 S和 D之间的分布差异，直接优化模型，从而准确定位身体关节的标注点。

3.3 Loss Function

2D人体姿态估计需要定位多个身体关节。因此，需要为每个身体关节构造各自的suppliers，demanders 和 cost function，之后通过测量相应 suppliers 和 demanders 间的分布差异（计算Earth Mover’s Distance）来计算每个人体关节对应的损失值。K表示总身体关节数，$L_k$ 表示 k-th 身体关节计算的loss，则损失函数定义如下：

3.4 Training and Testing

本文提出的方法可以应用于现成的2D人体姿态估计器中，训练期间通过最小化等式5中的损失函数来优化预测热图。测试期间，对于每个身体关节，先从预测的热图中选择具有最大像素值和的4个相邻像素的一个 square，然后将这四个像素值的和归一化为1。这4个像素的标准化像素值可以视为它们各自需要的 units of mass。 因此，以与第3.2节中从 demander 获得GT标注点坐标的相同方式获得该关节的预测坐标：$(x_i,y_i)$表示i-th选定像素的坐标，并标准化该像素值为$d_i$，i∈ {1, 2, 3, 4}，则该关节的预测坐标为：$(x_{pred},y_{pred})=(d_1\times x_1+d_2\times x_2+d_3\times x_3+d_4\times x_4,d_1\times y_1+d_2\times y_2+d_3\times y_3+d_4\times y_4)$

4 Analysis

本节分析大多选择MSE进行优化的热图姿态估计方法。输入图像 I 的总关节数为：K，$H_{dot}=\{H_{dot}^1,...,H_{dot}^K\},H_{Gau}=\{H_{Gau}^1,...,H_{Gau}^K\},H_{pred}=\{H_{pred}^1,...,H_{pred}^K\}$ 分别表示输入图像相应的 K个GT dot-annotated 热图，GT Gaussian-smoothed 热图和预测热图。${\mathcal{D}}_{dot}=\{(I,H_{dot})\}$ 表示输入图像和相应 K 张 dot-annotated 热图的K个关节分布，${\mathcal{D}}_{Gau}=\{(I,H_{Gau})\}$ 表示输入图像和相应 K 张 Gaussian-smoothed 热图的K个关节分布，$l_{MSE}(a,b)=||a-b|{|}_2^2$ 表示 pixel-wise MSE loss，$\varphi (I)=H_{pred},\varphi 是模型参数$。预测热图和GTdot-annotated 热图间计算的期望 risk 表示为：

预测热图和GT Gaussian-smoothed 热图间计算的期望 risk 表示为：

定理 1： $R(D_{dot},\varphi ,l_{MSE})和R(D_{Gau},\varphi ,l_{MSE})$ 间的关系可以表示为：

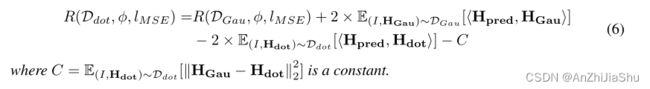
最小化 $H_{pred}和H_{Gau}$间的pixel-wise loss时， $R(D_{Gau},\varphi ,l_{MSE})$ 减小，式6的第二项增加，第三项不能确定增加或减少，因此不能保证$R(D_{dot},\varphi ,l_{MSE})$会减小，那么以此方式优化预测热图，定位身体关节的模型性能可能不会改善。更直观的分析如下：大多基于热图法的优化过程中，由于预测热图中所有H×W像素都会被计算损失，如图1所示，学习拟合其他像素而非标注点像素也会减少损失，因此，最小化整体像素损失不能确保优化模型性能。此外，训练过程中使用高斯 blub 构建GT 平滑高斯热图，因此在测试过程中，预测热图在标注点周围的高斯圆可能很大，如图3所示，不利于精确定位身体关节点。
我们的方法通过最小化从预测热图构建的分布（S）与从标注点构建的分布（D）间的差异，从新颖的角度优化预测热图。训练期间，由于我们将每对supplier 和 demander 间的成本函数表示为它们的L2距离，因此通过最小化分布差异可以将预测热图中的像素值聚集到标注点，因此最小化分布差异可以直接改进模型性能。此外，测试期间，配备将预测像素值聚集到标注点的机制可以实现更紧凑的身体关节定位，如图3所示。

图3：我们的方法将预测热图的优化表述为分布匹配问题，以及使用平滑高斯热图作为优化目标的baseline 的定性结果。如图所示，我们的方法能更紧凑定位身体关节。

5 Experiments

5.1 COCO Keypoint Detection

选择Simple Baseline, HRNet, and HRFormer做backbone，训练遵循它们各自的训练设置。为使用Sinkhorn算法计算 Earth Mover’s Distance，在实验中将Sinkhhorn熵正则化参数设置为1，并将Sinkhhor迭代次数设置为1000。

表1：当我们的方法应用于各种baseline时，在 COCO val set上的改进。

表2：当我们的方法应用于各种baseline时，在 COCO test-dev上的改进。

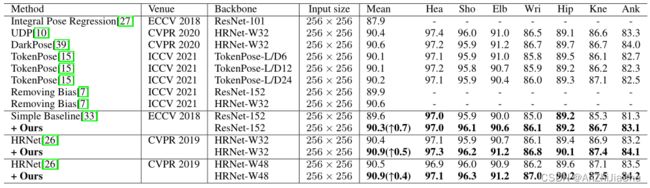
5.2 MPII Human Pose Estimation

表3：当我们的方法应用于各种baseline时，在 MPII val set上的改进。

5.3 Ablation Studies

以 HRNet-W48 作backbone，在coco val set上作消融实验。
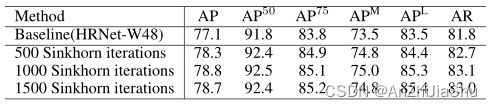
公式化D中引入 sub-pixel 概念的影响。 结果如表4所示：

表4: 包含sub-pixel分辨率概念的 demanders D 的有效性评估

Sinkhorn迭代次数的影响。 结果如表5所示：

表5：对Sinkhorn迭代次数的评估。

定性结果。一如图3所示，通过将 cost 函数公式化为L2距离，可以将预测热图中的像素值聚集到标注点，从而得到比依赖平滑高斯的baseline更紧凑的身体关节位置，表明我们的方法可以有效优化模型定位身体关节的精度。

6 Conclusion

本文从一个新的角度出发，将预测热图的优化公式化为预测热图和标注点之间的分布匹配问题。我们提出的方法简单有效，易于应用于各种2D人体姿态估计模型中。
这篇文章跟DSNT那篇文章有些类似，都是将GT热图跟预测热图之间的MSE转换为两个分布之间的匹配问题。