Fast Planner 轨迹规划

Robust and Efficient Quadrotor Trajectory Generation for Fast Autonomous Flight

0 概览

在本文中，提出了一种强大且高效的四旋翼运动规划系统，用于在 $3D$ 复杂环境中进行快速飞行。采用运动学动力学路径搜索方法在离散化控制空间中寻找安全、运动动力学可行且时间最短的初始轨迹。我们通过 B 样条$（B-Spline）$优化提高了轨迹的平滑度和间隙，该优化结合了来自欧几里德距离场 $(EDF)$ 的梯度信息和有效利用 $B$ 样条的凸包特性的动态约束。最后，通过将最终轨迹表示为非均匀 $B$ 样条，采用迭代时间调整方法来保证动态可行和非保守的轨迹。

1 关键问题

• 有限的时间和有限的机载计算机算力的情况下，现有的工作方法无法保证以高成功率生成符合安全和动力学运动学约束的可行轨迹
• 轨迹生成的效率和鲁棒性是必不可少的，在许多情况下，例如在未知环境中高速飞行的四旋翼飞机，应该在很短的时间内不断地重新生成轨迹以避免紧急威胁。
• 其次，为了确保生成的运动学动力学可行性，对速度和加速度的约束通常是保守的。因此，生成的轨迹的启发性/侵略性$（Aggressiveness）$通常很难调整以满足需要高飞行速度的应用。
• 提出了一种完整且鲁棒的在线轨迹生成方法来系统地解决这两个问题。采用基于启发式搜索和线性二次最小时间控制的动力学路径搜索。 它在离散化控制空间中有效地搜索安全、可行和最短时间的初始路径。然后在精心设计的 $B$ 样条优化中细化初始路径，该优化利用 $B$ 样条的凸包属性来合并梯度信息和动态约束。它改进了初始路径并快速收敛到平滑、安全和动态可行的轨迹。最后，将轨迹表示为非均匀 $B$ 样条，为此研究了导数控制点与时间分配之间的关系。在此基础上，采用迭代时间调整方法，将不可行的速度和加速度从轮廓中挤出，同时避免保守约束。
• 总结：

1. 安全性、动态可行性和攻击性/启发性/侵略性$（Aggressiveness）$是自下而上构建的
2. 提出了一种基于 $B$ 样条的凸包属性的优化公式，该公式巧妙地结合了梯度信息和动态约束，快速收敛得以生成平滑、安全和动态可行的轨迹
3. 研究了导数控制点与非均匀 $B$ 样条的时间分配之间的关系，应用基于关系的时间调整方法来保证可行和非保守运动$（Feasible$ $and$ $non-conservative$ $motion）$

2 相关工作

1. 非常有代表性的就是硬约束方法，也就是$Minimum$ $Snap$方法，其中轨迹表示为分段多项式，并通过求解二次规划 $(QP)$ 问题生成。具体方法的推导可以看我的这篇Blog，其中轨迹表示为分段多项式，并通过求解二次规划( $Quadratic$ $Programming,$ $QP$)问题生成。硬约束方法通过凸形式保证全局最优性。然而，忽略了自由空间中与障碍物的距离，这往往导致轨迹接近障碍物。此外，动力学约束是保守的，使轨迹速度不足，以快速飞行。
2. 文章（Polynomial Trajectory Planning for Aggressive Quadrotor Flight in Dense Indoor Environments）通过在迭代过程中添加中间路点的办法，来确保轨迹的安全性，然后轨迹生成优化的方法还是$Minimum$ $Snap$方法
3. 接着演化成了由一系列球体，多面体，立方体所形成的自由空间，在这个可行域内进行凸优化，并且提出了一种$B$样条的动力学搜索来找到初始轨迹，然后通过弹性优化方法进行优化，使用均匀 $B$ 样条可确保动态可行性，但会产生保守运动（$conservative$ $motion$）。这些方法的一个共同缺点是轨迹的时间分配是由简单的启发式给出的，然而，选择不当的时间分配会显着降低轨迹的质量。此外，只有通过迭代添加更多约束和求解二次规划问题才能获得可行的解决方案，这对于实时应用来说是不可取的。
4. 为了解决以上时间分配的问题，高老师提出了一种方法来搜索具有良好分配时间的路径（使用快速行进法和伯恩斯坦基多项式的四旋翼在线安全轨迹生成），并通过优化保证轨迹的安全性和动力学可行性。硬约束方法通过凸优化公式确保全局最优性，自由空间中到障碍物的距离被忽略，这往往导致轨迹接近障碍物。此外，动力学约束是保守的，使得轨迹的速度不足，无法快速飞行。
5. 软约束方法：还有一些方法将轨迹生成公式化为考虑平滑性和安全性的非线性优化问题。 通过使用梯度下降法最小化其平滑度和碰撞成本来生成离散时间轨迹，但优化是通过无梯度采样方法解决的。 后序方法将它们扩展到连续时间多项式轨迹，由于时间参数化是连续的，避免了数值微分误差并且更准确地表示四旋翼的运动。但是，成功率很低。为了解决这个问题，接着后序方法首先使用基于采样的路径搜索方法（类似RRT*）找到无碰撞的初始路径，该路径作为非线性优化的全局高质量优化的初始猜测，从而提高成功率。后序轨迹被参数化为均匀 $B$ 样条。由于 $B-Spline$ 本质上是连续的，因此无需显式地强制执行连续性，从而减少了约束的数量。由于其局部性，它对于局部重新规划也特别有用。软约束方法利用梯度信息将轨迹推离障碍物（类似APF方法），但受到局部最小值的影响，并且无法保证成功率和动力学可行性。我们的优化方法还利用梯度信息来提高轨迹的安全性。然而，与以前沿轨迹计算复杂的线积分的方法不同，该公式基于 $B$ 样条的凸包特性进行了重新设计，使其更简单，极大地提高了计算效率和收敛速度。
6. 综上，软约束方法利用梯度信息推动轨迹远离障碍物，但存在局部极小问题，没有很强的成功率和动力学可行性保证。此优化方法还利用梯度信息提高了轨迹的安全性。然而，与以往计算昂贵的沿轨迹线积分的方法不同，基于$B$样条的凸包特性，将公式设计得更加简单。它大大提高了计算效率和收敛速度。

3 $Fast-Planner$

3.1 前端路径搜索

• 前端运动动力学路径搜索模块为混合A*算法。该方法能够在栅格地图当中规划出一条安全的并且是符合动力学约束的一条可行轨迹。具体可以看我的这一篇Blog，如下图所示：

---

---

• 而且继承了$A\ast$启发式算法的特性
• 所谓的混合$AStar$算法就是将$A\ast$与$LatticeGraph$相关联，什么是$LatticeGraph$呢？
• 如下所示

---

---

• 这些弯弯的线，就是上图找到路径的那条轨迹旁的弯弯的线
• 所以将$A\ast$算法往这上面一套，就是混合$A\ast$
• 对传统的$$A\ast$算法进行改进，与之不同的是，$HybridA\ast$ 是在连续坐标系下进行启发式搜索，并且能够保证生成的轨迹满足无人机的非完整性约束
• 但算法运行过程中该路径并不一定是全局最优（这里的全局最优解指的是由传统$A\ast$ 算法生成的）的，但是经过试验，几乎为全局“次优”
• $A\ast$ 是赋予每个网格的中心点相应的损失并且算法只访问这些中心点，而$HybridA\ast$ 是先在这些网格中挑选满足UAV的3D连续状态的点，并将损失赋值给这些点
• 如下，左边那副图，只选择中间点，就是传统的$A\ast$，右边那副图，选择栅格内几乎所有的点，要满足UAV的运动学约束，并且连续状态

---

---

3.2 $Kinodynamic$ $Path$ $Searching$ 伪代码

---

• 这个算法不仅仅会考虑节点位置还会考虑其节点的速度和加速度

• 在算法流程图当中，$P$和$C$指的是开集和并集，与无人机动力学相关的$motion$ $primitives$不是直线而是$graph$ $edge$，$nodes$被用来记录$primitive$，以及$primitivesends$以及$g_c$和$f_c$成本
• $primitives$通过$Expand()$进行迭代$voxel$网格映射，除具有最小$f_c$（最小成本）的$voxel$外，那些以相同$voxel$结束的$voxel$将会被进行剪枝（$Prune()$）操作
• 综上，总的步骤就是：

1. 进行实时采样，离散获得轨迹节点（PVA三条件，轨迹节点，起始点速度，加速度）
2. 设置算法搜索参数
3. 将以上条件转为栅格，计算对应的成本
4. 进行迭代循环
5. 路径搜索，看当前节点是否到达目标点，没有的话就要进行进行扩张以及剪枝
6. 规划所得的路径

---

3.3 Code解读

3.3.1 fast_planner_node

• 在这个部分，先注册ROS节点，看下方的ros::init(argc, argv, "fast_planner_node");
• 以及进行类的实例化TopoReplanFSM topo_replan; KinoReplanFSM kino_replan;。

#include 
#include 

#include 
#include 

#include 
namespace backward {
backward::SignalHandling sh;
}

using namespace fast_planner;

int main(int argc, char** argv) {
  ros::init(argc, argv, "fast_planner_node");
  ros::NodeHandle nh("~");

  int planner;
  nh.param("planner_node/planner", planner, -1);

  TopoReplanFSM topo_replan;
  KinoReplanFSM kino_replan;

  if (planner == 1) {
    kino_replan.init(nh);
  } else if (planner == 2) {
    topo_replan.init(nh);
  }

  ros::Duration(1.0).sleep();
  ros::spin();

  return 0;
}

3.3.2 kino_replan_fsm

• 从下方这几行代码，可以看出是在订阅无人机的目标点的信息以及位置信息

for (int i = 0; i < waypoint_num_; i++) {
    nh.param("fsm/waypoint" + to_string(i) + "_x", waypoints_[i][0], -1.0);
    nh.param("fsm/waypoint" + to_string(i) + "_y", waypoints_[i][1], -1.0);
    nh.param("fsm/waypoint" + to_string(i) + "_z", waypoints_[i][2], -1.0);
  }

• 设置了ROS当中的定时器，定时地进行回调

  exec_timer_   = nh.createTimer(ros::Duration(0.01), &KinoReplanFSM::execFSMCallback, this);
  safety_timer_ = nh.createTimer(ros::Duration(0.05), &KinoReplanFSM::checkCollisionCallback, this);

• 利用下方定义的$exe{c}_{s}tate$判断是否等待目标点，看是否需要进行重新规划

  if (exec_state_ == WAIT_TARGET)
    changeFSMExecState(GEN_NEW_TRAJ, "TRIG");
  else if (exec_state_ == EXEC_TRAJ)
    changeFSMExecState(REPLAN_TRAJ, "TRIG");

3.3 成本函数

• 实际成本与启发式成本，由于目标是找到一条在时间和控制成本上最优的轨迹，将轨迹的成本定义为：
  $$\mathcal{J}(T)={\int }_0^T\Vert \mathbf{u}(t){\Vert }^{2}dt+\rho T$$
• 在成本函数当中，
• 通过最小值原理计算出一个封闭形式的轨迹，该轨迹最小化从当前状态$x_c$到目标状态$x_g$的$\mathcal{J}(T)$，也就是当前状态到终点的成本
• 为了找到最小化的成本最佳时间$T$，采用如下方法：

1. 因为轨迹可以进行多项式的表示，将多项式表示写成矩阵的形式
   $$\mathbf{p}(t):={\left[p_x(t),p_y(t),p_z(t)\right]}^{\top },p_{\mu }(t)=\sum _{k=0}^K{a}_k{t}^k$$
   $$\begin{array}{rl}{p}_{\mu }^{\ast }(t)& =\frac{1}{6}{\alpha }_{\mu }{t}^3+\frac{1}{2}{\beta }_{\mu }{t}^2+v_{\mu c}+p_{\mu c}\\ \left[\begin{array}{c}{\alpha }_{\mu }\\ {\beta }_{\mu }\end{array}\right]& =\frac{1}{T^3}\left[\begin{array}{cc}-12& 6T\\ 6T& -2T^2\end{array}\right]\left[\begin{array}{c}{p}_{\mu g}-p_{\mu c}-v_{\mu c}T\\ v_{\mu g}-v_{\mu c}\end{array}\right]\\ {\mathcal{J}}^{\ast }(T)& =\sum _{\mu \in \{x,y,z\}}\left(\frac{1}{3}{\alpha }_{\mu }^2{T}^3+{\alpha }_{\mu }{\beta }_{\mu }{T}^2+{\beta }_{\mu }^{2}T\right)\end{array}$$
2. 其中 $p_{\mu c},v_{\mu c},p_{\mu g},v_{\mu g}$ 是当前和目标的位置以及速度，$\mu \in \{x,y,z\}$。${\mathcal{J}}^{\ast }(T)$是成本函数。为了找到最小化成本的最佳时间 $T$，将 ${\alpha }_{\mu },{\beta }_{\mu }$ 代入${\mathcal{J}}^{\ast }(T)$ 并找到 $\frac{\partial {\mathcal{J}}^{\ast }(T)}{\partial T}=0$ 的根。最小成本 $\min {\mathcal{J}}^{\ast }$ 和可行轨迹的根是选择并表示为 $T_h$。我们使用 ${\mathcal{J}}^{\ast }\left(T_h\right)$ 作为启发式 $h_c$。最后，$f_c$ 定义为：
   $$f_c=g_c+h_c=g_c+{\mathcal{J}}^{\ast }\left(T_h\right)$$

3.4 B-Spline轨迹优化

• 路径搜索产生的路径可能是次优的（这是因为混合A*所得到的路径并非是最优的路径）。此外，由于自由空间中的距离信息被忽略，这条路径通常靠近障碍物，如下图所示。因此，在建议的 $B$ 样条优化中提高了路径的平滑度和间隙。利用均匀 $B$ 样条的凸包特性，将来自欧几里得距离场的梯度信息和动态约束结合起来，使其在很短的时间内收敛，从而生成平滑、安全和动态可行的轨迹。

使用基于梯度的数值优化来变形轨迹。红色和绿色曲线是初始路径和优化后的 $B$ 样条。黄点代表 $B$ 样条的控制点。由于忽略了距离信息，初始路径靠近障碍物，而 $B$ 样条被基于梯度的优化推开。

3.4.1 均匀的B样条

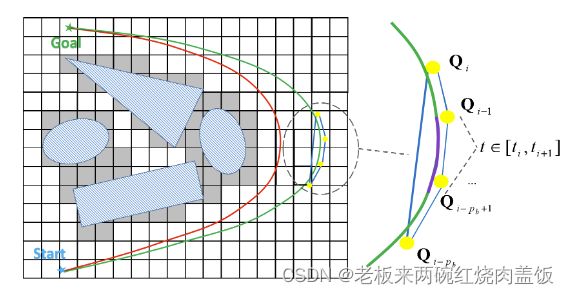
• $B$样条是一个分段多项式，由其次数$p_b$、一组 $N+1$ 个控制点 $\left\{{\mathbf{Q}}_0,{\mathbf{Q}}_1,\cdots ,{\mathbf{Q}}_N\right\}$和一个节点向量 $\left[t_0,t_1,\cdots ,t_M\right]$唯一确定，其中 ${\mathrm{Q}}_i\in {\mathbb{R}}^3,t_m\in \mathbb{R}$和$M=N+p_b+1$。$B$ 样条轨迹由时间 $t$ 参数化，其中 $t\in \left[t_{p_b},t_{M-p_b}\right]$。对于均匀的 $B$ 样条，每个节点跨度 $\Delta t_m=t_{m+1}-t_m$ 具有相同的值 $\Delta t$。为了评估 时间$t\in \left[t_m,t_{m+1}\right)\subset \left[t_{p_b},t_{M-p_b}\right]$ 处的位置，我们首先对 $t$进行归一化，$s(t)=\left(t-t_m\right)/\Delta t$，然后可以使用矩阵表示评估位置：
  $$\begin{array}{rl}& \mathbf{p}(s(t))=\mathbf{s}(t{)}^{\top }{\mathbf{M}}_{p_b+1}{\mathbf{q}}_m\\ & \mathbf{s}(t)={\left[\begin{array}{lllll}1& s(t)& s^2(t)& \cdots & s^{p_b}(t)\end{array}\right]}^{\top }\\ & {\mathbf{q}}_m={\left[\begin{array}{lllll}{\mathbf{Q}}_{m-p_b}& {\mathbf{Q}}_{m-p_b+1}& {\mathbf{Q}}_{m-p_b+2}& \cdots & {\mathbf{Q}}_m\end{array}\right]}^{\top }\end{array}$$

• 这里 ${\mathbf{M}}_{p_b+1}$ 是由 $p_b$ 确定的常数矩阵。在我们的实现中，$p_b$ 设置为 $3$。导数的评估完全相同，因为 $B$ 样条的导数也是 $B$ 样条。 $B$ 样条的凸包特性对于设计优化公式至关重要，对于确保整个轨迹的动态可行性和安全性非常有用。

3.4.2 凸包特性

• B样条的凸包特性就不过多介绍了，曲线总是被包含在一个凸包之中

4 时间调整

尽管在路径搜索和优化中限制了动力学可行性，但有时会得到不可行的轨迹。基本原因是梯度信息倾向于拉长整体轨迹，同时将其推离障碍物较远。因此，四旋翼飞行器必须更积极地飞行，以便在同一时间内行进更长的距离，如果原始运动已经接近物理极限，这不可避免地会导致过度激进的运动。
为了保证动态可行性，采用基于导数控制点与非均匀B样条的时间分配（节点跨度）之间的关系的时间调整方法。由于这些关系，可以通过调整相关的时间分配来改变预期的飞行轨迹攻击性（aggressiveness），因此可以在没有过度保守约束的情况下确保动态可行性。

4.1 迭代时间调整伪代码

---

---

5 总结

利用$B$样条的凸包特性，结合欧几里得距离场的梯度信息和动态约束，采用$B$样条优化算法提高了轨迹的光滑性和间隙。最后，通过将最终轨迹表示为非均匀$B$样条，采用迭代时间调整方法保证轨迹的动态可行性和非保守性。