卫统课笔记(摸鱼)②:T-test
t-test 的条件
①变量服从正态分布
②样本数<50
③样本均数比较时具有方差齐
方差齐性是统计学中的一个经典概念,其本质意义是说,对于两个或多个我们将要检验或分析的总体其数据具有散布程度特点的一致性程度。一般来说,可以将其形象理解为总体一的数据分布疏密胖瘦与总体二的数据分布疏密胖瘦的一致性程度。
t-test的三种类型
1.单样本t检验
用样本代替一个未知总体和一个已知总体进行比较
2.配对t检验
配对设计,无关变量相近的两样本组成一对。
计算对子差值,作为新样本(服从正态分布,总体均数0)
3.两独立样本的t检验
从两个不同总体(都服从正态分布,有方差齐性)随机抽样,组成两个样本
检验两个样本代表的总体均数是否相等。
单侧假设检验和双侧假设检验
由t-test算得t值,先确定类型是双侧还是单侧检验后,再确定t对应的P.val(双侧的p值是单侧的p值的2倍)
双侧假设检验概念:对于一些不能根据已有情报知道两比较总体均数的大小关系的变量(比如xx避孕药对血细胞数目的影响,不能根据常识知道差异一定是偏大或是偏小),H1假设为μ1≠μ2
在t分布上,表现为可信概率面积由线μ=μ0向两侧(μ<μ0&&μ>μ0)延伸,故称为双侧检验
单侧假设检验概念:对于一些根据常理就能摸清两比较总体具体的差异(比如演艺圈发量总体μ1和医学圈发量总体μ2,肯定是μ2<μ1)
关于T-test结果的看法
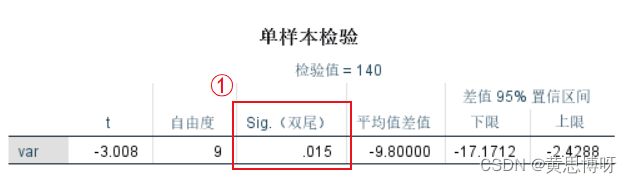
在SPSS中,是直接给出t对应的双侧P.val:
对于置信区间1-α=95%,直接用得到的双尾P.val(图框①)和α/2(即0.025)进行比较。
(例如我们进行双侧检验,那么这里的P.val=0.015<0.025,有统计学意义,拒绝H0,接受H1,认为两总体之间有差异)
在课本里的做法,没有去求样本t值的P.val,而是查表找0.05对应的t值,进行t值之间的比较。
还是用这个结果,t0=3.008,自由度(df)=9,查表。
注意:得到单侧S=0.05的t值ts=1.833,双侧S=0.05的t值td=2.262。
对于类型为双侧检验,比较得t0>td,说明P.val<0.025,结果有统计学意义,拒接H0,接受H1,两总体均数之间有差异。
SPSS里的操作:
单样本的t检验:
1.输入样本数
2.点击【分析】-->【比较均值】-->【单样本检验】打开操作窗口
3.转入变量
4.输入已知总体均数
5.点击确定
差分的 95% 置信区间
t df Sig.(双侧) 均值差值 下限 上限
2.040 19 .056 9.17800 -.2390 18.5950双侧的P值:0.056,双侧检验无统计学意义,但是单侧t检验P.val=0.056/2=0.028<0.05,有统计学意义。
两独立样本的t检验:
输入组变量(定义好值标签)和数据变量
点击【分析】-->【比较均值】-->【独立样本t检验】打开弹窗。
输入检验变量和组变量到不同的操作栏
确定分组值(对应同一个group值的属于同一组),点击继续
最后点击确定。
结果查看:根据方差齐性分为两列(方差齐&&方差不齐)
查看方差齐性的P.val
若是P.val<0.05说明两总体方差不齐,t-test的结果看方差不齐的那一列。
确定类型为单侧检验还是双侧检验,确定结果的P.val需不需要x2
若是选择单侧检验,且P.val*2>0.05,说明没有统计学意义,不拒接H0,尚不能说明结果无差异。
进行方差齐性检验
从健康人中随机抽取10人检测血清转铁蛋白(TF)含量,和从肝炎患者从随机抽得的12名患者的血清转铁蛋白含量。分成两个变量(TF&&group)
group TF
1.00 272.64
1.00 267.42
1.00 263.79
1.00 269.85
1.00 274.52
1.00 289.46
1.00 283.84
1.00 276.98
1.00 263.90
1.00 269.88
2.00 224.67
2.00 230.91
2.00 247.05
2.00 230.40
2.00 249.93
2.00 230.60
2.00 248.00
2.00 218.26
2.00 232.05
2.00 247.65
2.00 232.01
2.00 219.91点击【分析】-->【比较平均值】-->【单因素ANOVA检验】
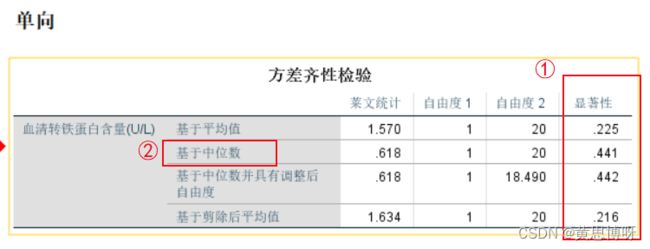
①框内输入TF变量,②框内输分组变量,点击框③【确定】
结果看显著性(框①),若是>0.05,接受两个总体具有方差齐性。
一般查看【基于中位数】(框②)这一栏目。
文件拆分和恢复:
①【数据】-->【拆分文件】-->弹窗内选择【比较组】
输入分组索引值变量,点击确定。
再进行【分析】-->【探索】
②【数据】-->【拆分文件】-->弹窗内选择【分析所有个案,不建立组】
输入分组索引值变量,点击确定。