吴恩达机器学习课后作业——偏差和方差

诊断偏差和方差

一、作业内容

在练习的前半部分，您将实现正则化线性回归，利用水库水位的变化来预测从大坝流出的水量。在下半部分中，您将对调试学习算法进行一些诊断，并检查偏差和偏差的影响。

本次的数据是以.mat格式储存的，x表示水位的变化，y表示大坝的出水量。数据集共分为三部分：训练集（X, y）、交叉验证集（Xval, yval）和测试集（Xtest, ytest）。

数据集下载位置(包含吴恩达机器学课后作业全部数据集)：data

二、作业分析

1、实现正则化线性回归，使用其来研究具有不同偏差-方差属性的模型。

2、当模型不理想的时候，通常也就是分为两种情况：偏差问题（欠拟合问题）和方差问题(过拟合问题）。

3、如何区分模型是高偏差还是高方差：
(1) 高偏差的模型（欠拟合），通常会表现为训练误差比较高，且交叉验证误差约等于训练误差。
(2)高方差的模型（过拟合），通常会表现为训练误差比较低，且且交叉验证误差远大于训练误差。

4、高偏差和高方差的解决思路：
高方差：
(1) 采集更多的样本数据
(2) 减少特征数量，去除非主要的特征
(3) 增加正则化参数λ
高偏差：
(1) 引入更多的相关特征
(2) 采用多项式特征
(3) 减少正则化参数λ

5、正则化项是如何影响偏差和方差问题的
正则化线性回归中代价函数的公式：

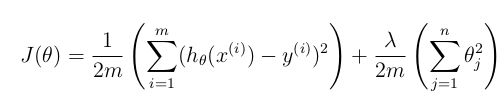
惩罚系数λ过大时，会导致欠拟合，会出现高偏差的现象。
惩罚系数λ过小时，会导致过拟合，会出现高方差差的现象。

6、如何选择合适的惩罚函数λ
首先要分别定义好假设函数，训练集、交叉验证集和测试集的代价函数

假设函数：

训练集代价函数：

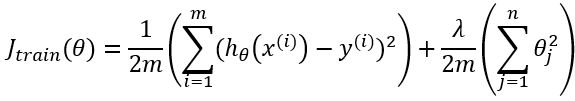
交叉验证集代价函数：

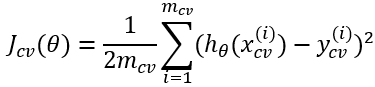
测试集的代价函数：

**注意：**对于训练集，我们为了获得更好的假设函数，所以在代价函数中需要加入正则化项。但是对于交叉验证集和测试集的代价函数，则不需要加入正则化项。

训练集、验证集、测试集的比例一般为6:2:2

训练数据集：训练模型；（习得模型的参数）

验证数据集：验证模型的效果；如果模型的效果不好，则重新调整参数再次训练新的模型，直到找到了一组参数，使得模型针对验证数据集来说已经达到最优了；（将每个训练集训练好的参数在交叉验证集上计算交叉验证误差，选择误差最小的那个假设作为我们的模型，这里是用来选择λ）

测试数据集：将此数据集传入由验证数据集得到的最佳模型，得到模型最终的性能；（作为衡量最终模型性能的数据集）

7、如何选择正则化参数λ

(1) 根据不同的λ分别计算训练集代价函数，得到最优的${\theta }^i$

(2) 根据交叉验证集，计算每一种模型的交叉验证集代价函数，选出表现最好的模型

(3) 对于第二步选择的模型，利用测试集测试模型的泛化能力。

8、我们通常会利用学习曲线去判断一个算法是否处于偏差、方差问题，或者是二者皆有。对于学习曲线，我们会采用训练样本逐渐增多的方法来进行可视化。

9、对于高偏差的模型：

当模型出现高偏差的时候，随着样本数量的增大，训练集误差会逐渐增大，交叉验证集误差会逐渐下降。但是最后两者会比较接近。

当模型出现高偏差的时候，增大数据量对于模型的改进意义不大，因为误差是比较大的。

对于高方差的模型：

当模型出现高方差的时候，随着样本数量的增大，训练集误差会逐渐增大，但是并不会太大。交叉验证集误差会逐渐下降。

当模型出现高方差的时候，增大数据量是存在一定的意义的，可以在这方面尝试努力

10、小型神经网络计算量比较小，但是容易出现欠拟合现象；大型神经网络拟合效果会比较好，但是计算量比较大，容易出现过拟合现象。所以一般会选用较大型的神经网络，因为即使出现过拟合现象，也可以使用正则化的方式进行修正。

11、为了平衡样本的特征值量级，我们通常会使用特征缩放的方法。

12、特征缩放(Feature Scaling)
特征缩放的几种方法：
(1) 最大最小值归一化(min-max normalization)：将数值范围缩放到[0,1]区间里

(2) 均值归一化(mean normalization)：将数值范围缩放到[-1,1]区间里，且数据的均值变为0

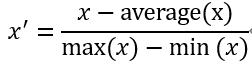
(3) 标准化 / z值归一化(standardization / z-score normalization)：将数值缩放到0附件，且数据的分布变为均值为0，标准差为1的标准正态分布（先减去均值来对特征进行中心化 mean centering 处理，再除以标准差进行缩放）

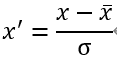
(4) 最大绝对值归一化(max abs normalization)：也就是将数值变为单位长度(scaling to unit length)，将数值范围缩放到[-1,1]区间里

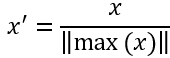
13、归一化和标准化的区别：

归一化（normalization）：归一化是将样本的特征值转换到同一量纲下，把数据映射到[0,1]或者[-1, 1]区间内。

标准化（standardization）：标准化是将样本的特征值转换为标准值（z值），每个样本点都对标准化产生影响。

14、归一化、标准化的好处：

在机器学习算法的目标函数(例如SVM的RBF内核或线性模型的l1和l2正则化)，许多学习算法中目标函数的基础都是假设所有的特征都是零均值并且具有同一阶数上的方差。如果某个特征的方差比其他特征大几个数量级，那么它就会在学习算法中占据主导位置，导致学习器并不能像我们说期望的那样，从其他特征中学习。

15、归一化和标准化的对比分析

(1) 标准化更好保持了样本间距。当样本中有异常点时，归一化有可能将正常的样本“挤”到一起去。比如三个样本，某个特征的值为1,2,10000，假设10000这个值是异常值，用归一化的方法后，正常的1,2就会被“挤”到一起去。如果不幸的是1和2的分类标签还是相反的，那么，当我们用梯度下降来做分类模型训练时，模型会需要更长的时间收敛，因为将样本分开需要更大的努力。而标准化在这方面就做得很好，至少它不会将样本“挤到一起”。

(2) 标准化更符合统计学假设。对一个数值特征来说，很大可能它是服从正态分布的。标准化其实是基于这个隐含假设，只不过是略施小技，将这个正态分布调整为均值为0，方差为1的标准正态分布而已。

三、代码实战

引入所需函数库

import numpy as np
import scipy.io as sio
import scipy.optimize as opt
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns

创建一个加载数据的函数

# 加载数据
def load_data():
    # d['X'] shape = (12, 1)
    d = sio.loadmat('ex5data1.mat')
    return map(np.ravel, [d['X'], d['y'], d['Xval'], d['yval'], d['Xtest'], d['ytest']])

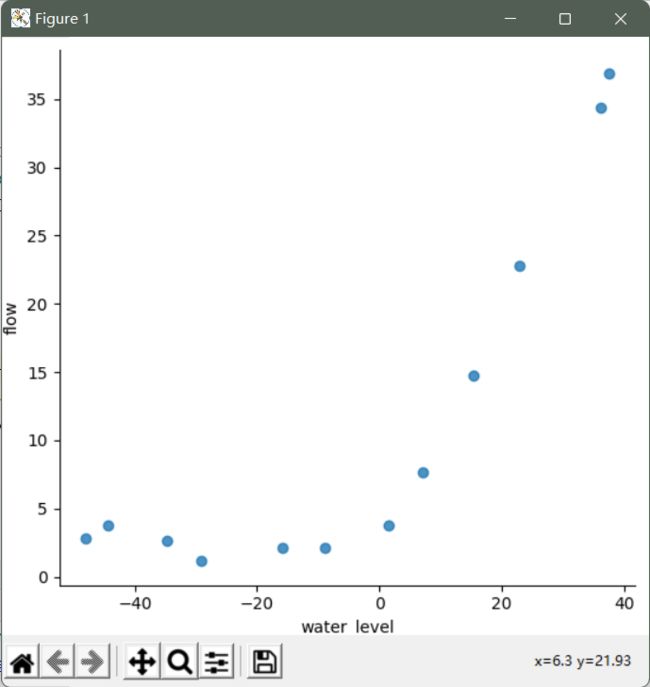
绘图查看数据分布：

df = pd.DataFrame({'water_level':X, 'flow':y})
sns.lmplot('water_level', 'flow', data=df, fit_reg=False, size=7)
plt.show()

创建代价函数

# 代价函数
def cost(theta, X, y):
    m = X.shape[0]

    inner = X @ theta - y
    square_sum = inner.T @ inner
    cost = square_sum / (2 * m)

    return cost

将代价函数正则化

# 正则化代价函数
def regularized_cost(theta, X, y, learningRate):
    m = X.shape[0]

    regularized_term = (learningRate / (2 * m)) * np.power(theta[1:], 2).sum()

    return cost(theta, X, y) + regularized_term

创建梯度函数

# 梯度
def gradient(theta, X, y):
    m = X.shape[0]
    inner = X.T @ (X @ theta - y)   #(m,n).T @ (m, 1) -> (n, 1)

    return inner / m

将梯度函数正则化

# 正则化梯度
def regularized_gradient(theta, X, y, learningRate):
    m = X.shape[0]

    regularized_term = theta.copy()     # 和theta相同的形状
    regularized_term[0] = 0     # don't regularize intercept theta
    regularized_term = (learningRate / m) * regularized_term

    return gradient(theta, X, y) + regularized_term

神经网络训练参数并可视化λ=0时拟合的线性方程

# 拟合数据
# 正则化项  = 0
# 线性回归模型
def linear_regression_np(X, y, learningRate):
    # 初始化theta
    theta = np.ones(X.shape[1])

    # 开始训练
    res = opt.minimize(fun=regularized_cost, x0=theta, args=(X, y, learningRate), method='TNC', jac=regularized_gradient, options={'disp': True})

    return res

# 加载数据
X, y, Xval, yval, Xtest, ytest = load_data()

learningRate = 0
X, Xval, Xtest = [np.insert(x.reshape(x.shape[0], 1), 0, np.ones(x.shape[0]), axis=1) for x in (X, Xval, Xtest)]
theta = np.ones(X.shape[1])
final_theta = linear_regression_np(X, y, learningRate).get('x')
b = final_theta[0]  # intercept
m = final_theta[1]  # slope

# 绘制图像
plt.scatter(X[:,1], y, label = "Training data")
plt.plot(X[:,1], X[:,1] * m + b, label = "Prediction")
plt.legend(loc = 2)
plt.show()

拟合曲线显示拟合的不是很好，从学习曲线可以看出存在高偏差问题

若二者损失都大且差距不明显，则设定的模型过于简单，无法很好的拟合数据，存在欠拟合问题。

使用训练集的子集来拟合应模型

注意：1、使用训练集的子集来拟合模型
2、在计算训练代价和交叉验证代价时，没有用正则化
3、记住使用相同的训练集子集来计算训练代价

training_cost, cv_cost = [], []

m = X.shape[0]
for i in range(1, m+1):
    res = linear_regression_np(X[:i, :], y[:i], learningRate)
    tc = regularized_cost(res.x, X[:i, :], y[:i], learningRate)
    cv = regularized_cost(res.x, Xval, yval, learningRate)

    training_cost.append(tc)
    cv_cost.append(cv)

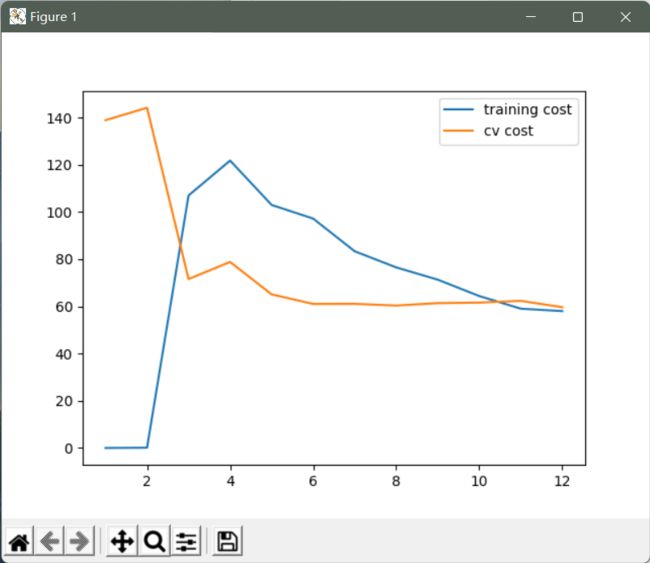
# 绘制图像
plt.plot(np.arange(1, m+1), training_cost, label='training cost')
plt.plot(np.arange(1, m+1), cv_cost, label='cv cost')
plt.legend(loc=1)
plt.show()

这个模型拟合不太好, 欠拟合了

特征映射创造多项式特征，进行多项式回归，用更复杂的函数去拟合

准备多项式回归数据
1、扩展特征到8阶，或者你需要的阶数
2、使用归一化来合并$x^n$
3、不要忘了截断term

# 创建多项式特征
def prepare_poly_data(*args, power):
    # 继续输入X，Xval或Xtest将以相同的顺序返回
    def prepare(x):
        # 扩展功能
        # 增加多项式，从x的平方到x的多次方
        df = poly_features(x, power=power)

        # 标准化
        ndarr = normalize_feature(df).iloc[:,:].values

        # 添加拦截term
        return np.insert(ndarr, 0, np.ones(ndarr.shape[0]), axis=1)

    return [prepare(x) for x in args]

使用 归一化 来合并$x^n$

# 增加多项式，从x的平方到x的多次方
def poly_features(x, power, as_ndarray=False):
    data = {'f{}'.format(i): np.power(x, i) for i in range(1, power + 1)}
    df = pd.DataFrame(data)

    return df.iloc[:,:].values if as_ndarray else df

def normalize_feature(df):
    # 沿着DataFrame的输入轴(默认0)应用函数
    return df.apply(lambda column: (column - column.mean()) / column.std())

画出学习曲线

# 画出学习函数
def plot_learning_curve(X, y, Xval, yval, learningRate):
    training_cost, cv_cost = [], []
    m = X.shape[0]

    for i in range(1, m + 1):
        # 采用正则化方法拟合参数
        res = linear_regression_np(X[:i, :], y[:i], learningRate)

        # 计算这里的代价时，计算的是非正则化代价函数。 正则化只用于拟合参数
        tc = cost(res.x, X[:i, :], y[:i])
        cv = cost(res.x, Xval, yval)
        training_cost.append(tc)
        cv_cost.append(cv)

    plt.plot(np.arange(1, m + 1), training_cost, label='training cost')
    plt.plot(np.arange(1, m + 1), cv_cost, label='cv cost')
    plt.legend(loc=1)

加载数据并拓展特征值

X, y, Xval, yval, Xtest, ytest = load_data()
X_poly, Xval_poly, Xtest_poly= prepare_poly_data(X, Xval, Xtest, power=8)

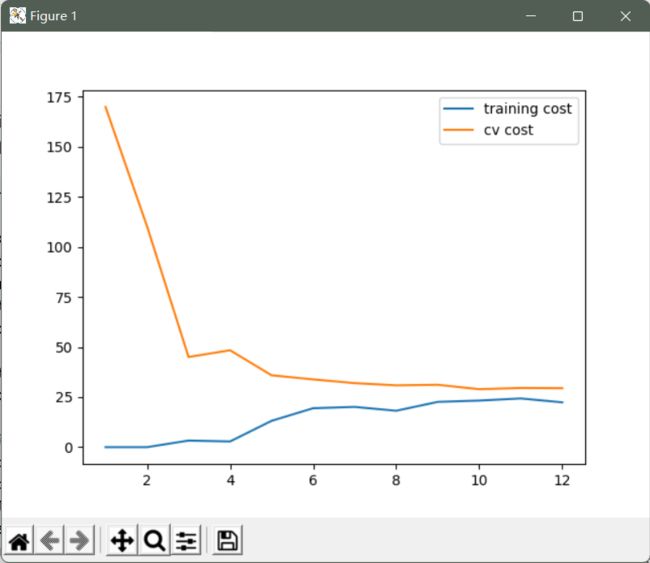
通过绘出学习图像选择合适的λ

首先，我们没有使用正则化，所以 = 0

learningRate = 0
plot_learning_curve(X_poly, y, Xval_poly, yval, learningRate)
plt.show()

我们可以看出训练的代价太低了，不真实. 这是 过拟合了

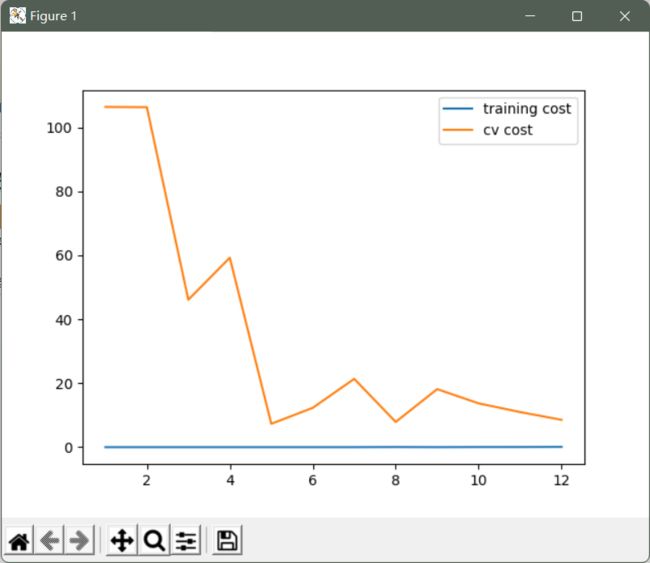
尝试 = 1，减轻过拟合

learningRate = 1
plot_learning_curve(X_poly, y, Xval_poly, yval, learningRate)
plt.show()

训练代价增加了些，不再是0了。 也就是说我们减轻过拟合

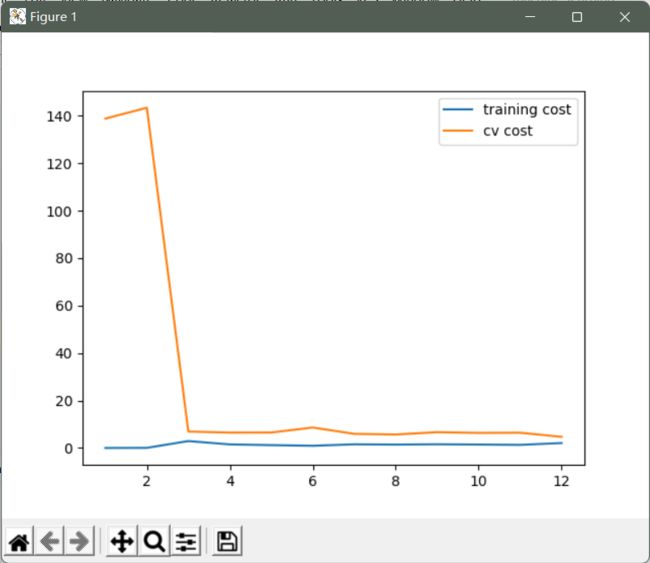
尝试 = 100

learningRate = 100
plot_learning_curve(X_poly, y, Xval_poly, yval, learningRate)
plt.show()

太多正则化了。变成了欠拟合状态

为了找到最佳的λ，我们列出一个λ列表，通过训练数据集和交叉验证集来找出最优λ

l_candidate = [0, 0.001, 0.003, 0.01, 0.03, 0.1, 0.3, 1, 3, 10]
training_cost, cv_cost = [], []

for learningRate in l_candidate:
    res = linear_regression_np(X_poly, y, learningRate)
    # 计算训练集上的误差
    tc = cost(res.x, X_poly, y)
    # 计算验证集上的误差
    cv = cost(res.x, Xval_poly, yval)

    training_cost.append(tc)
    cv_cost.append(cv)

绘制出不同 取值下训练集和交叉验证集的损失

# 不同  取值下训练集的损失
plt.plot(l_candidate, training_cost, label='training')
plt.plot(l_candidate, cv_cost, label='cross validation')
plt.legend(loc=2)

plt.xlabel('lambda')

plt.ylabel('cost')
plt.show()

拿到最佳的λ

b_l = l_candidate[np.argmin(cv_cost)]

使用测试集训练代价函数

for learningRate in l_candidate:
    theta = linear_regression_np(X_poly, y, learningRate).x
    print('test cost(l={}) = {}'.format(learningRate, cost(theta, Xtest_poly, ytest)))

调参后， = 0.3 是最优选择，这个时候测试代价最小

test cost(l=0) = 10.804375286491785
test cost(l=0.001) = 10.911365745177878
test cost(l=0.003) = 11.265060784108712
test cost(l=0.01) = 10.879143763702967
test cost(l=0.03) = 10.022378551698187
test cost(l=0.1) = 8.631776100446476
test cost(l=0.3) = 7.3365081011786275
test cost(l=1) = 7.466282452677015
test cost(l=3) = 11.643940740451052
test cost(l=10) = 27.715080273166386

参考链接：https://github.com/fengdu78/Coursera-ML-AndrewNg-Notes
https://blog.csdn.net/weixin_41799019/article/details/118055103?spm=1001.2014.3001.5502