数值计算大作业：拉格朗日插值多项式（PS：其他数值计算大作业我也打包发出来了，包含详细程序注释。大家可以免费下载交流）

   作为研究生的入门课，数值计算的大作业算是所有研究生开学的重要编程作业。

   相较于普通的拉格朗日插值法的程序，我把整个算法在MATLAB中整合成了一个多功能的M函数文件，包括等距节点插值、随机节点插值 、二次插值以及切比雪夫零点插值 ,具体lagrange.m的程序放在文章最后了，需要的同学自取。下文为作业详解

题目：给定函数 ，x在区间[-1,1]上完成以下工作

数学原理：一般地，若已知在互不相同n+1个点处的函数值（即该函数过这n+1个点），则可以考虑构造一个过这n+1个点的、次数不超过n的多项式,使其满足多项式在特征点的结果与此点的函数值相等。要估计任一点ξ，ξ≠xi,i=0,1,2,...,n,则可以用Pn（ξ）的值作为准确值f(ξ)的近似值，此方法叫做“插值法”。

因此本题中进行插值的拉格朗日插值多项式为，在定义域区间使用的n+1个点进行n次插值并最后得到的插值多项式为。

为了方便实验中多个问题的画图，利用MATLAB软件编写了针对本实验可实现多种模式进行插值的函数 lagrange.m并放在附录中了。函数说明如下

function [plotx,Y,Lout]=lagrange(model,xmin,xmax,n,plotx)

输入：model为插值模式;xmin,xmax为插值多项式起始点;n为插值次数（若使用模式4，由切比雪夫不等式特性默认插值区间为[-1,1]，否则自己变化插值域）；计算函数为f(x)=1/(1+25*x^2);plotx为画图的范围,一维向量

输出：plotx同上，只是画图的范围；Y,Lout为两个输出矩阵，Y(i)为在横坐标为plotx(i)下的f(x)值，Lout(i)为在选择计算模式为model=*，在横坐标为plotx(i)下的插值结果(model=1,为第一问等距节点Lagrange插值多项式；model=2,为第二问随机产生节点的插值多项式；model=3,为第三问二次插值函数；model=4,为第四问的切比雪夫插值零点进行插值；)

下面所有图像蓝色的曲线为原函数，红色图像为插值函数

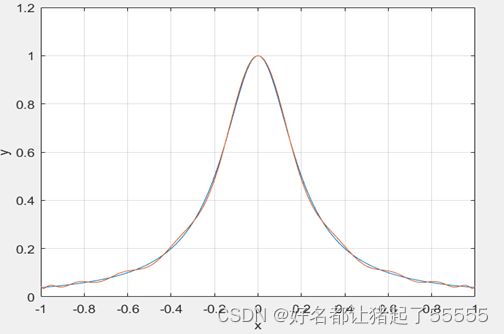
1.利用11个等距节点做10次Lagrange 插值多项式L(x)，在同一坐标系下绘出f(x)和L(x)的图像，观察发生的现象。若将插值多项式的次数提高到20，结果又将如何？

第一问用11个等距节点在区间[-1，1]进行10次拉格朗日插值，并在[-1,1]区间以0.01间隔作图的的命令如下,

[x,y,l]=lagrange(1,-1,1,10,[-1:0.01:1]);
 plot(x,y,x,l);
grid on
xlabel('x');
ylabel('y');

用11个等距节点在区间[-1，1]进行20次拉格朗日插值，并分别在[-0.5,0.5]区间以0.01间隔和[-1,1]区间以0.01间隔作图的的命令如下,

[x,y,l]=lagrange(1,-1,1,20,[-0.5:0.01:0.5]);

%[x,y,l]=lagrange(1,-1,1,20,[-1:0.01:1]);

 plot(x,y,x,l)

grid on

xlabel('x');

ylabel('y');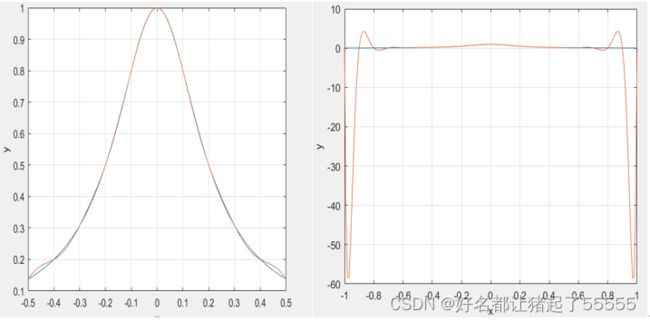

10次等距拉格朗日插值在[-1,1]画图

20次等距拉格朗日插值分别在[-0.5,0.5]和[-1,1]画图

结论：根据上述两种等距插值方法绘制的插值曲线可以看出，即使中间区间进行20次拉格朗日插值的逼近效果较好，但是总体偏差反倒更大了。因此拉格朗日插值插值的次数并非次数N越高逼近f（x）的精度越好，而是插值次数越大，龙格现象越明显。

2.随机产生19个[-1,1]之间的实数，再加上区间的两个端点，构造20次Lagrange插值多项式，在同一坐标系下绘出f(x)和L(x)的图像，该插值函数是否振荡？

第二问用21个随机节点在区间[-1，1]进行20次拉格朗日插值，并在[-1,1]区间以0.01间隔作图的的命令如下,

[x,y,l]=lagrange(2,-1,1,20,[-1:0.01:1]);

 plot(x,y,x,l)

grid on

xlabel('x');

ylabel('y');

20次随机取点进行拉格朗日插值在[-1,1]的图像

结论：由（1）知，20次拉格朗日插值的龙格现象很严重，但是由本题的随机取插值点X可以看出在负区间取点较多且在-1处较密，因此图像在负区间龙格现象比正区间龙格现象明显，而正区间插值逼近效果较好。

3.利用11个等距节点计算f(x)的分段二次插值函数，并绘图，观察发生的现象。

第三问命令如下,

[x,y,l]=lagrange(3,-1,1,10,[-1:0.01:1]);

plot(x,y,x,l)

 grid on

 xlabel('x');

 ylabel('y');

11个等距节点计算分段二次插值在[-1,1]的图像

结论：低次数的拉格朗日插值虽然精度不高，但是由于没有龙格现象，因此在插值节点间隔较小的分段区间，逼近f(x)的效果反倒较好。

4.利用n=10,20,40次切比雪夫多项式的零点为插值节点，构造Lagrange插值多项式，在同一坐标系下绘出f(x)和L(x)的图像，观察插值多项式是否振荡，并对观察到的现象给予简单的解释。

第四问命令如下,

 [x,y,l]=lagrange(4,-1,1,10,[-1:0.01:1]);

% [x,y,l]=lagrange(4,-1,1,20,[-1:0.01:1]);

%[x,y,l]=lagrange(4,-1,1,40,[-1:0.01:1]);

plot(x,y,x,l);grid on xlabel('x'); ylabel('y');

N=10次切比雪夫多项式的零点为插值节点的插值图像

N=20次切比雪夫多项式的零点为插值节点的插值图像

N=40次切比雪夫多项式的零点为插值节点的插值图像

结论：由李庆扬版数值计算第5版教材P62定理6可知，若设Tn(x)是首项系数为1的切比雪夫多项式，则Tn(x)是所有满足函数逼近的正交多项式Hn(x)中最大值最小的多项式。利用此结论，可以得出切比雪夫多项式是最佳（一致）逼近多项式。利用切比雪夫多项式的零点插值，可以推出插值误差最小化的结论。

      上面三个图分别利用n=10,20，40次切比雪夫多项式的零点为插值节点，构造Lagrange插值多项式进行插值.可见分别比n=10等距拉格朗日插值和分段二次插值，n=20随机取点和等距拉格朗日插值效果好的多。甚至使用n=40次切比雪夫多项式的零点为插值节点，得到的图像几乎和原函数f(x)图像重合。

附录：Matlab软件自己编译的拉格朗日多模式插值函数程序

%lagrange.m
%拉格朗日插值多项式
function [plotx,Y,Lout]=lagrange(model,xmin,xmax,n,plotx)
% 输入：model为插值模式，xmin,xmax为插值多项式起始点，n为插值次数（若使用模式4，则默认插值区间为[-1,1]，否则自己变化插值域）；计算函数为f(x)=1/(1+25*x^2);plotx为画图的范围,一维向量
% 输出：plotx同上，只是为了；Y,Lout为两个输出矩阵，Y(i)为在横坐标为plotx(i)下的f(x)值，Lout(i)为在选择计算模式为model，在横坐标为plotx(i)下的插值结果
% model=1,为第一问等距节点 Lagrange 插值多项式；model=2,为第二问随机产生节点的插值多项式；model=3,为第三问二次插值函数；model=4,为第四问的切比雪夫插值零点进行插值；
    m=length(plotx);
           %  选择计算模式，模式判断中的A矩阵为计算插值向量过程中使用的过渡矩阵
            switch model
                case 1
                 %模式1为插值次数为n的平均拉格朗日插值，X为n+1维的行向量
                    step=(xmax-xmin)/n;
                    X=[xmin:step:xmax];
                case 2
                  %模式2为插值次数为n的在[xmin,xmax]范围的随机拉格朗日插值函数，X为n+1维的行向量
                      A=sort(-1+2*rand(1,n-1));
                      X=zeros(1,n+1);
                      X(1)=-1;X(n+1)=1;
                       for i=1:n-1
                          X(i+1)=A(i);
                       end
                case 3
                %模式3为第三问，为便于程序设计，只能计算[-1,1]的5段均分二次插值函数题
                    X=[-1:0.2:1];
                    n=10;
                case 4
                % 模式4就是利用切比雪夫零点进行插值，插值区间和节点次数选取同上
                T=@(x,y) cos(pi*(2*x-1)/(2*(y+1)));
                X=zeros(1,n+1);
                 for i=1:n+1
                      X(i)=T(i,n);
                 end
                 X=sort(X);
            end      
% 计算X1到Xn+1的插值XN向量            
XN=zeros(1,n+1);
 f=@(x)1/(1+25*x^2);
            for i=1:n+1
              XN(i)=f(X(i));
            end
%  原函数绘制
     Y=plotx;
     for i=1:m
         Y(i)=f(plotx(i));
      end
%  系数矩阵
 h1 = ones(n,1);
 h2 = ones(1,1);
 h3 = ones(2,1);
%  Lout为a向量插值后的结果向量，可直接画图用
 Lout=zeros(1,m);
 lout=zeros(1,1); 
            if model~=3
                      for j=1:m
                         % 对横坐标plotx，利用给定模式进行插值计算
                        for i=1:n+1
                          Xq = X([1:i-1 i+1:n+1]);
                          lout = lout + XN(i)*prod((h1*plotx(j)-Xq'*h2)./(X(i)-Xq'*h2));
                        end
                        Lout(j)=lout;
                        lout=0;
                      end    
                    
            elseif model==3
                  for j=1:m
                         % 将插值域分为5部分，分别为[-1,-0.8,-0.6],[-0.6,-0.4,-0.2].....[0.6,0.8,1],画图用的点，落在哪里，就用哪个区间计算结果
                         %因为当画图点取-1时，interval=ceil((plotx(j)+1)*2.5);使得结果等于0，数组索引数出错，故单独将画图点x=-1放置在区间1中
                        interval=ceil((plotx(j)+1)*2.5);
                            if interval==0
                                interval=1;
                            end
                            interval=interval*2+1;
                        Xq = X([interval-2,interval-1,interval]);
                            for i=1:3
                              Xq1 = Xq([1:i-1 i+1:3]);
                              lout = lout + f(Xq(i))*prod((h3*plotx(j)-Xq1'*h2)./(Xq(i)-Xq1'*h2));
                            end
                        Lout(j)=lout;
                        lout=0;
                   end     
            end
    end

% 画图函数
% [x,y,l]=lagrange(1,-1,1,10,[-1:0.01:1]);
% plot(x,y,x,l)
% grid on
% xlabel('x');
% ylabel('y');