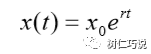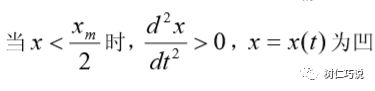logistic模型matlab代码_人口增长模型

点击关注不迷路！！！

      世间万物均有规律可循，从第一个人类诞生到现在70多亿的人口世界，人口的增长同样有规律可循，据考古学家论证，地球上出现生命距今已有 20 亿年，而人类的出现距今却不足 200 万年。纵观人类人口总数的增长情况，我们发现：1000 年前人口总数为 2.75 亿。经过 漫长的过程到 1830 年，人口总数达 10 亿，又经过 100 年，在 1930 年，人口总数达 20 亿；30 年之后，在 1960 年，人口总数为 30 亿；又经过 15 年，1975 年的人口总数是 40 亿，12 年之后即 1987 年，人口已达 50 亿。 

我们自然会产生这样一个问题：人类人口增长的规律是什么？

我们先来做一些假设：

设x(t)表示t时刻的人口数，且 x(t)连续可微。人口的增长率r 是常数(增长率=出生率—死亡率)。人口数量的变化是封闭的，即人口数量的增加与减少只取决于人口中个体的生育和死亡，且每一个体都具有同样的生育能力与死亡率。 

所以就有：

很简单的倒数定义:

其解为：

所以这就是一个非常基础又简单的人口增长模型，但是很显然这个模型有弊端，哪里呢，没错就是对于自然增长率，前面我们对于自然增长率r估计偏大，所以预测出的人口也会偏大，所以接下来我们对r进行修正。

我们知道，地球上的资源是有限的，它只能提供一定 数量的生命生存所需的条件。随着人口数量的增加，自然资源、环境条件等对人口再增长的限制作用将越来越显著。如果在人口较少时，我们可以把增长率r 看成常数，那么当人口增加到一定数量之后，就应当视r 为一个随着人口的增加而减小的量，即将增长率r 表示为人口x(t)的函数r(x)，且 r(x)为 x的减函数。 

设r(x)为x的线性函数，r(x)=r-sx

自然资源与环境条件所能容纳的大人口数为Xm,当x=Xm时，自然增长率为0

接下来用到的都是高数知识啊：

上式为可分离变量方程，其解为：

再求二阶导：

接下来我们就可以讨论一下：

当0

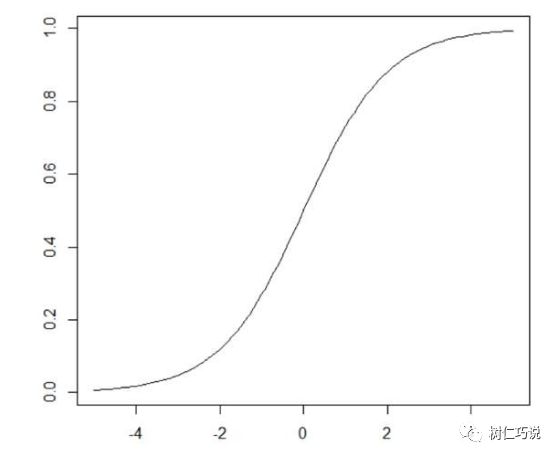
反之，其为凸，人口增长率会在x=xm/2时取到最大值，即人口总数达到极限值一半以前是加速生长时期，经过这一点之后，生长速率会逐渐变小，终达到零。张这样： 

怎么样，是不是很眼熟，对在高中生物中我们学到过S型曲线，其原理跟这个完全一致，这个模型有个名字叫——Logistic模型，其实它更多时候会以Logistic回归模型的形式出现，logistic回归又称logistic回归分析，是一种广义的线性回归分析模型，常用于数据挖掘，疾病自动诊断，经济预测等领域。例如，探讨引发疾病的危险因素，并根据危险因素预测疾病发生的概率等。以胃癌病情分析为例，选择两组人群，一组是胃癌组，一组是非胃癌组，两组人群必定具有不同的体征与生活方式等。因此因变量就为是否胃癌，值为“是”或“否”，自变量就可以包括很多了，如年龄、性别、饮食习惯、幽门螺杆菌感染等。自变量既可以是连续的，也可以是分类的。然后通过logistic回归分析，可以得到自变量的权重，从而可以大致了解到底哪些因素是胃癌的危险因素。同时根据该权值可以根据危险因素预测一个人患癌症的可能性。在计算机领域它更多的是被用于一种二分类工具。

      所以大家在以后预测某种类似于S型增长的规律的数据就可以采用logistic阻滞增长模型，话不多说，上MATLAB代码：

 syms a b;c = [a b]';A = [25, 23, 29, 44, 84, 164,332,521, 970, 1623, 2454, 3213, 3623, 3743, 3943, 4045, 4460, 4440];n = length(A);for i = 2:n    H(i) = A(i) - A(i - 1);endH(1) = [];for i = 2:n    C(i) = (A(i) + A(i-1))/2;endC(1) = [];D = [-C; C.^2];Y = H; Y = Y';c = inv(D*D')*D*Y;c = c';a = c(1); b = c(2);F = []; F(1) = A(1);for i = 2:(n+n)    F(i) = (a*A(1))/(b*A(1)+(a - b*A(1))*exp(a*(i-1)));enddisp('预测数据为：');F%绘制曲线图t1 = 0:n-1; t2 = 0:2*n-1;plot(t1, A, 'ro'); hold on;plot(t2, F);xlabel('t'); ylabel('s');legend('实际数量','预测数量');grid on;

大家可以改变A去进行自己所需要的预测内容即可。

总结一下，阻滞增长模型在一定程度上可以预测出人口的增长规律，但实际中是非常复杂的，要将很多其他影响人口变化因素引入的话是非常的复杂，有待进一步去研究，所以大家本期只需学会通过阻滞增长模型去进行相关数据预测就可以啦！

本期内容就到此结束啦，感谢您的阅读，快快关注公众号“树仁阅读”

创作属实不易，点个关注，点亮在看，帮忙转发一下增长人气也是非常感谢！树仁巧说与您下期再见！