Meta-learning
基本理解
meta learning翻译为元学习,也可以被认为为learn to learn
元学习与传统机器学习的不同在哪里?
元学习与传统机器学习, 这里举个通俗的例子,拿来给大家分享?
-
把训练算法类比成学生在学校学习,传统的机器学习任务对应的是每个科目上分别训练一个模型,而元学习是提高学生的整体学习能力,学会学习。
-
学校中,有的学科各科成绩都很好,有的学生却普遍存在偏科的现象。
-
各科成绩都很好,说明各科的元学习能力强,学会了如何学习,可以迅速使用不同科目的学习任务。
-
偏科学生元学习能力较弱,只能某一科学习成绩较好,换门科就不行了,不会举一反三,触类旁通。
现在经常使用的深度学习网络是偏科生。分类和回归对应的网络模型完全不同,即使同样是分类任务,把人脸识别的网络架构用在分类ImageNet数据上**,也未必能达到很高的准确率**。
还有一个不同点:
- 传统的深度学习方法都是从头开始学习(训练),即learning for scratch。对算力和时间都是更大的消耗和考验。
- 元学习强调的是从不同的若干小任务和小样本来学习一个对未知样本未知类别都有好的判别和泛化能力的模型。
基本思想
写在前面,图片均来自对李宏毅老师的教学视频。

对图1的解释:
Meta learning 有称为learn to learn。是说让机器学习学会学习,拥有学习的能力。
元学习的训练样本和测试样本都是基于任务的,通过不同类型的任务训练模型,更新模型参数,掌握学习技巧。然后举一反三,更好地学习其他任务。比如:任务1是语音识别、任务2是图像识别。 ⋯ \cdots ⋯任务100是文本分类。任务101与前面的100个任务模型均不同,训练任务即为这100个不相同的任务,测试任务为第101个。

对图2的解释:
在机器学习中,训练样本的训练集称为train set 测试集称为test set。 元学习广泛应用于小样本学习中,在元学习中,训练样本的训练集称为$support set , 训 练 样 本 的 测 试 集 叫 做 ,训练样本的测试集叫做 ,训练样本的测试集叫做query set$.
注意:在机器学习中,只有一个大样本数据集,将这个一个大数据集分成两部分,称为train set test set。
但是在元学习中,不只有一个数据集,有多少个不同的任务,就有多少个数据集,然后每个数据集又分成两个部分:分别称为:
s u p p o r t s e t 和 q u e r y s e t support set和query set supportset和queryset.
这里没有考虑验证集:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-i3ZaLzEw-1669718326587)(https://img-加粗样式blog.csdnimg.cn/img_convert/19d51bbe90254071612ea8ac627eb2bb.webp?x-oss-process=image/format,png#pic_center)]
图3 为传统深度学习操作方式:即:
- 定义一个网络结构
- 初始化参数
- 通过自己选择优化器来更新参数
- 通过两次epoch进行参数更新》
- 得到网络的最终输出。
元学习与传统深度学习联系在哪里?
图3中红色方框的东西是认为设计的,即我们常说的超参数。
而元学习的目标都是去自动学习或者说代替放宽中的东西,不同的代替方式就发明出不同的元学习算法。
- 图4简单介绍了元学习的原理:
-
- 在神经网络算法,都需定义一个损失函数来评价模型的好坏,元学习的损失都是通过 N N N个任务的测试损失相加的,定义在第 N N N个任务的测试损失相加是 l n l^n ln.对于 N N N个任务来说,
- 总的损失为: L ( F ) = ∑ n = 0 n l n L(F) = \sum^n_{n = 0}l^n L(F)=∑n=0nln,这就元学习的优化目标。
假设两个任务 T a s k 1 Task1 Task1和 T a s k 2 Task2 Task2,通过训练任务1,得到任务1的损失函数 l 1 l_1 l1,通过训练任务2,得到任务2损失为 l 2 l_2 l2,然后将这两个任务损失函数相加,得到整个训练任务的损失函数,即图4右上角的公式。
如前文对元学习的了解不够,后面还有更加详细的解释。
Meta learning的算法有很多,有的高大上的算法可以i针对不同的训练任务,输出不同的神经网络结构和超参数。例如:
$ Neural Architecture Search (NAS) 和 AutoML 。 这 些 算 法 大 多 都 相 当 复 杂 , 我 们 普 通 人 难 以 实 现 , 另 外 一 种 比 较 容 易 实 现 M e t a l e a r n i n g 算 法 , 就 是 本 文 要 介 绍 的 。这些算法大多都相当复杂,我们普通人难以实现,另外一种比较容易实现Meta learning算法,就是本文要介绍的 。这些算法大多都相当复杂,我们普通人难以实现,另外一种比较容易实现Metalearning算法,就是本文要介绍的MAML 和 Reptile$。不改变深度神经网络结构,只改变网络的初始化参数。
MAML
理解MAML算法的损失函数的含义和推导过程。首先的与pre-trainiing区分开来。
对图5的解释:
我们定义初始化参数为 ϕ \phi ϕ,其初始化参数为 ϕ 0 \phi_0 ϕ0,定义在第 n n n个测试任务上,训练之后的模型参数为 θ n ^ \hat{\theta^n} θn^,于是MAML的总损失函数为: L ( ϕ ) = ∑ n = 1 n l n ( θ n ^ ) L(\phi) = \sum^n_{n = 1}l^n(\hat{\theta^n}) L(ϕ)=∑n=1nln(θn^)
maml损失算法图解
MAL与pre-training有什么影响?
损失函数不同
MAML的损失函数为: L ( ϕ ) = ∑ n = 1 n l n ( θ n ^ ) L(\phi) = \sum^n_{n = 1}l^n(\hat{\theta^n}) L(ϕ)=∑n=1nln(θn^)
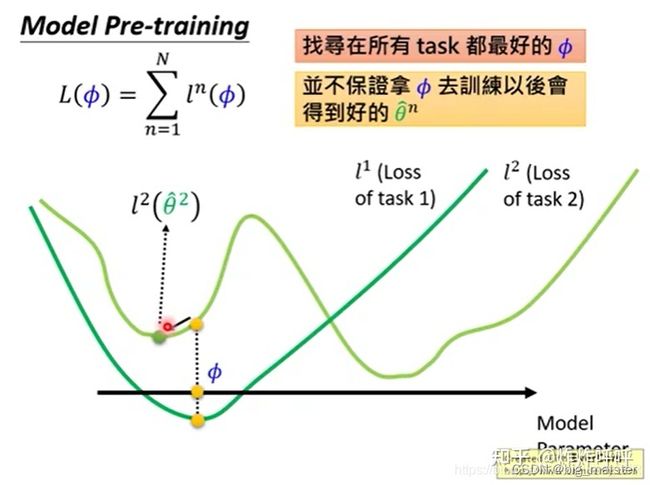
预训练的损失函数为: L ( ϕ ) = ∑ n = 1 n l n ( ϕ ) L(\phi) = \sum^n_{n = 1}l^n(\phi) L(ϕ)=∑n=1nln(ϕ)
直观上理解是MAML所测评的损失是在任务训练之后测试loss。而预训练直接在原有基础上球损失没有经过的训练。如图6所示:

优化思想不同
这里先分享以下,我们看到对损失函数的生动描述。
损失函数奥妙:初始化参数掌控全场,分任务参数各自为营。


李宏毅老师在这里举了个很生动比喻:
他把MAML比作选择读博,即更在意的是学生的以后的发展潜力;而model pre-training就相当于选择毕业直接去大厂工作,马上就把所学技能兑现金钱,在意的是当下表现如何。如图9所示。
- 计算速度快
- 所有更新参数步骤都被限制在了一次:级one -step。
- 在用这个算法时,即测试新任务的表现可以更新更多次。
- 适用于数据有限的情况。

MAML的工作机理

- Require1:task的分布,即随机抽取若干个task组成任务池
- Require2:step size是学习率,MAML基于二重梯度,每次迭代包括两次参数更新的过程,所以有两个学习率可以调整。
- 随机初始化模型的参数
循环,可以理解为一轮迭代过程或一个epoch - 随机对若干个task采样,形成一个batch。
- 对batch中的每一个task进行循环
- 对利用batch中的某一个task中的support set,计算每个参数的梯度。在N-way K-shot的设置下,这里的support set应该有NK个。(N-way K-shot意思是有N种不同的任务,每个任务有K个不同的样本)。
- 第一次梯度的更新。
结束第一次梯度更新 - 第二次梯度更新。这里用的样本是query set。步骤8结束后,模型结束在该batch中的训练,开始回到步骤3,继续采样下一个batch。
MAML的应用: Toy Example
Reptile 其算法图如下:
- 训练任务的网络可以更新多次。
- reptile不再项MAML一样计算梯度,而是直接用一个参数 ∈ \in ∈乘以meta 网络,与训练任务网络参数的差来更新meta 网络参数。
- 从效果看Reptile与,MAML基本持平。
以上为对元学习的深入理解,后续可能出MAML数学公式推导,感兴趣请点赞留言。
总结
慢慢的将各种元学习进一步的搞定,都行啦的样子与打算。
先大致了解一波,然后开始慢慢的研究元学习,并将其研究透彻。
全部都将其搞定都行啦的样子与打算。
总结
可以类比集成学习的方式来进行元学习的学习。












