吴恩达机器学习系列课程笔记——第七章:正则化(Regularization)
7.1 过拟合的问题
https://www.bilibili.com/video/BV164411b7dx?p=39
到现在为止,我们已经学习了几种不同的学习算法,包括线性回归和逻辑回归,它们能够有效地解决许多问题,但是当将它们应用到某些特定的机器学习应用时,会遇到过**拟合(over-fitting)**的问题,可能会导致它们效果很差。
在这段视频中,我将为你解释什么是过度拟合问题,并且在此之后接下来的几个视频中,我们将谈论一种称为**正则化(regularization)**的技术,它可以改善或者减少过度拟合问题。
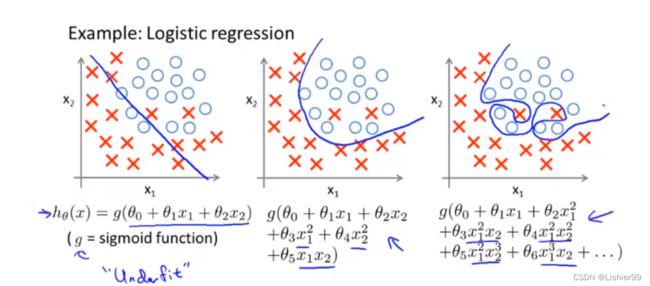
如果我们有非常多的特征,我们通过学习得到的假设可能能够非常好地适应训练集(代价函数可能几乎为0),但是可能会不能推广到新的数据。
第一个模型是一个线性模型,欠拟合,不能很好地适应我们的训练集;第三个模型是一个四次方的模型,过于强调拟合原始数据,而丢失了算法的本质:预测新数据。我们可以看出,若给出一个新的值使之预测,它将表现的很差,是过拟合,虽然能非常好地适应我们的训练集但在新输入变量进行预测时可能会效果不好;而中间的模型似乎最合适。
就以多项式理解,x 的次数越高,拟合的越好,但相应的预测的能力就可能变差。
问题是,如果我们发现了过拟合问题,应该如何处理?
- 丢弃一些不能帮助我们正确预测的特征。可以是手工选择保留哪些特征,或者使用一些模型选择的算法来帮忙(例如PCA)
- 正则化。 保留所有的特征,但是减少参数的大小(magnitude)。
7.2 代价函数
https://www.bilibili.com/video/BV164411b7dx?p=40
我们可以从之前的事例中看出,正是那些高次项导致了过拟合的产生,所以如果我们能让这些高次项的系数接近于0的话,我们就能很好的拟合了。 所以我们要做的就是在一定程度上减小这些参数$\theta $ 的值,这就是正则化的基本方法。我们决定要减少和的大小,我们要做的便是修改代价函数,在其中和 设置一点惩罚。这样做的话,我们在尝试最小化代价时也需要将这个惩罚纳入考虑中,并最终导致选择较小一些的和。 修改后的代价函数如下:
通过这样的代价函数选择出的和 对预测结果的影响就比之前要小许多。
假如我们有非常多的特征,例如x1、x2、x3…我们并不知道其中哪些特征我们要惩罚,我们将对所有的特征进行惩罚,并且让代价函数最优化的软件来选择这些惩罚的程度。这样的结果是得到了一个较为简单的能防止过拟合问题的假设:

注意:我们没有对θ0进行惩罚,实际上,两种情况没什么区别。
其中 λ 又称为正则化参数(Regularization Parameter)。
作用是:控制两个不同目标之间的取舍,控制两个目标的之间的平衡,从而使得目标函数尽可能的简单,避免出现过拟合的情况。
第一个目标:目标就是我们想去训练,想去更好地拟合数据,与目标函数的第一项有关(本职工作)。
第二个目标:我们要保持参数尽量地小,与目标函数第二项有关
(优化拟合程度)
经过正则化处理的模型与原模型的可能对比如下图所示:

如果选择的正则化参数 λ 过大,即对θ1θ2…惩罚太大,则会把所有的参数都最小化了,θ都接近0,导致模型变成 hθ( x ) = θ0,也就是上图中红色直线所示的情况,造成欠拟合,也就是偏见性太强,说明不太符合实际情况。
为了使正则化起到应有的效果,我们应该注意正则参数λ的取值,之后我们就会讲解如何取得一个合理的正规化参数λ,这就是高度正则化的思想。
回顾一下代价函数,为了使用正则化,让我们把这些概念应用到到线性回归和逻辑回归中去,那么我们就可以让他们避免过度拟合了。
7.3 正则化线性回归
https://www.bilibili.com/video/BV164411b7dx?p=41
对于线性回归的求解,我们之前推导了两种学习算法:一种基于梯度下降,一种基于正规方程。
如果我们要使用梯度下降法令这个代价函数最小化,因为我们未对进行正则化,所以梯度下降算法将分两种情形:
- 由于正则化时,是不对θ0进行操作的,所以我们在梯度下降算法中,也把θ0那一项剥离开来。
- 而对比线性方程的梯度算法,多出来的那一项实际上就是结合了正则化的后一项进行求偏导的值
然后对上面的算法中 j=1,2,…,n 时的更新式子进行调整可得:

通过调整后,可以发现一个有趣的值,就是前面这项,括号中的(1-α·λ/m),学习率一般很小,数据集m一般很大,λ是个正常的常数,所以括号的值应该略小于1,则前面这一项也就略小于θj,所以可以看出,正则化线性回归的梯度下降算法的变化在于,每次都在原有算法更新规则的基础上令值减少了一个额外的值。
我们同样也可以利用正规方程来求解正则化线性回归模型,方法如下所示:
正规方程就是在某些情况中可以使用正规方程直接求θ的最优解。
图中的矩阵尺寸为 (n+1)*(n+1),而且依旧不存在不可逆的情况(选看解析)。
7.4 正则化的逻辑回归模型
https://www.bilibili.com/video/BV164411b7dx?p=42
针对逻辑回归问题,我们在之前的课程已经学习过两种优化算法:我们首先学习了使用梯度下降法来优化代价函数,接下来学习了更高级的优化算法,这些高级优化算法需要你自己设计代价函数。之后就是使用代码,计算代价函数中关键的两个数据:J(θ)和J(θ)的偏导数。
回顾之前的逻辑回归代价函数

因为会出现过拟合的情况,所以使用正则化,加上了后面一项

所以对梯度下降的θ迭代也同样做出改变:

以上就是我们之前第七章的大致思路
同样对于逻辑回归,我们也给代价函数增加一个正则化的表达式,得到代价函数:

接下来我们就要代码来求出关键的两项,J(θ)和J(θ)的偏导数
Python代码:
import numpy as np
def costReg(theta, X, y, learningRate):
theta = np.matrix(theta)
X = np.matrix(X)
y = np.matrix(y)
first = np.multiply(-y, np.log(sigmoid(X*theta.T)))
second = np.multiply((1 - y), np.log(1 - sigmoid(X*theta.T)))
reg = (learningRate / (2 * len(X))* np.sum(np.power(theta[:,1:theta.shape[1]],2))
return np.sum(first - second) / (len(X)) + reg
注:看上去同线性回归一样,但是知道

所以与线性回归不同。 Octave 中,我们依旧可以用 fminuc 函数来求解代价函数最小化的参数,值得注意的是参数的更新规则与其他情况不同。 注意:
- 虽然正则化的逻辑回归中的梯度下降和正则化的线性回归中的表达式看起来一样,但由于两者的不同所以还是有很大差别。
- θ不参与其中的任何一个正则化。
接下来的课程中,我们将学习一个非常强大的非线性分类器,无论是线性回归问题,还是逻辑回归问题,都可以构造多项式来解决。你将逐渐发现还有更强大的非线性分类器,可以用来解决多项式回归问题。我们接下来将将学会,比现在解决问题的方法强大N倍的学习算法。