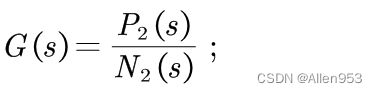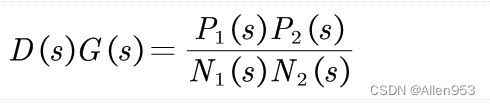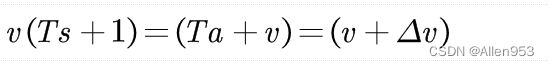频域法分析系统详解及个人笔记
目录
伯德图画的是闭环传函还是开环传函？
什么是最小相位环节？什么是非最小相位环节？
为什么说增加零点使相位超前而增加极点使相位滞后？
为什么说PD控制器抗扰能力比较弱？
为什么PD控制器对高频噪声这么敏感？
为什么说系统的幅频曲线要远离0度，相频曲线要远离-180度，系统才能稳定？
开环增益K有什么作用？
为什么一个积分环节的伯德图幅频曲线斜率恰恰是一个-20dB/dec？
系统的响应跟零点有关系吗？
相角裕度和幅值裕度的定义是怎么样的？
相角裕度和幅值裕度能说明什么？
伯德图上能否看出来低频开环增益是多少？如何保证足够的低频开环增益？
伯德图能否看出来系统的固有频率？
从伯德图如何判断是否发生共振？
相角滞后180度，系统一定不稳定吗？
共振一定会使得系统不稳定吗？
伯德图不能同时触碰0dB线和-180度线，这是什么意思？
如何判断一个控制器是超前补偿还是滞后补偿？
为什么超前控制器s+a中a越小超前角越大？
为什么一阶微分环节可以使得相位超前T秒？
为什么一阶惯性环节的输出比输入延迟时间常数T时间？
频率响应：系统对正弦信号的稳态响应。
正弦信号：正弦信号很好理解。
稳态响应：那么什么是稳态响应呢？就是说啊，我给一个系统输入一个正弦信号之后，系统不是马上输出一个最终的正弦信号的，系统是先进行动态响应，然后经过一段时间的动态响应，然后系统达到了稳态。这个时候系统输出的正弦信号，才是我们分析的对象。我们在频率特性里面分析的幅值比和相位差，就是说的这个时候达到稳态之后输出幅值和输入幅值得比，输出相位和输入相位的差。因为在系统达到稳态以前，输出的幅值和相位是在动态变化的，只有达到稳态，系统才输出稳定的正弦信号。
其实很简单，任何信号都能分解成很多不同频率的正弦波相加，然后不同频率的正弦波在被控对象上有不同的响应（就是不同频率的输入有不同比例的输出）不同频率在频域上就是一个点，所以经常在频域上分析你的被控对象的响应。
G(s)=-1的伯德图如下图所示：
伯德图画的是闭环传函还是开环传函？
伯德图画的是开环传递函数的图。这里和根轨迹是有区别的。
根轨迹分析对象是开环传递函数，但是画出来的根轨迹图是闭环传递函数的根的轨迹图像。
伯德图画的却是开环传递函数的幅频和相频特性。
我们可以做个实验看一下。
首先设一个系统的开环传递函数为 
则系统的闭环传递函数为
画出伯德图如下：
我们把图放大，可以看到在频率为0.102的时候，幅值响应为-6.03dB，而
也就是说这个时候
然后我们再在simulink搭建模型仿真，可以看到，开环传递函数
闭环传递函数
我们能够看到的是，当系统在开环情况下，系统实际响应幅值在0.5左右，跟原信号幅值1的比值刚好为0.5.
也就是说我们在上面画伯德图的时候，输入的是开环传递函数，画的就是开环传递函数的伯德图。
输入G(s)，画的就是G(s)的伯德图而非
de的伯德图。
什么是最小相位环节？什么是非最小相位环节？
为什么说增加零点使相位超前而增加极点使相位滞后？
从这个图上看 ，是同时增加了一个零点和极点。
我们分开讨论：
当增加了一个零点的时候，相当于引入了一个微分项， 而微分项有超前特性。比如说我想控制一个电机的转速达到期望，假设当转速较低时，角加速度却很大。
如果从速度上考虑，这个时候转速很低，应该给一个大电压让转速趋于期望，但是由于角加速度很大，如果我们给一个大电压，那么可能很快就有一个更大的超调量，然后再给一个更大的电压，产生更大的超调量，从而系统就不稳定，边震荡边发散了。
所以我们从速度的微分来考虑，也就是角加速度考虑，这个时候角加速度很大，而速度还很慢，但是我们已经知道了随着时间增加，速度会很快趋于期望，所以我们要给一个小的增益，让系统超调减少（可以看作增加了系统阻尼），从而让我们的控制器具备了前瞻性——即通过角加速度提前预测后面的转速。
为什么说PD控制器抗扰能力比较弱？
PD控制器就是单纯的给原来的系统增加了一个零件，然后让根轨迹落入合适的区域，那么为什么说PD控制器的抗扰能力比较弱呢？
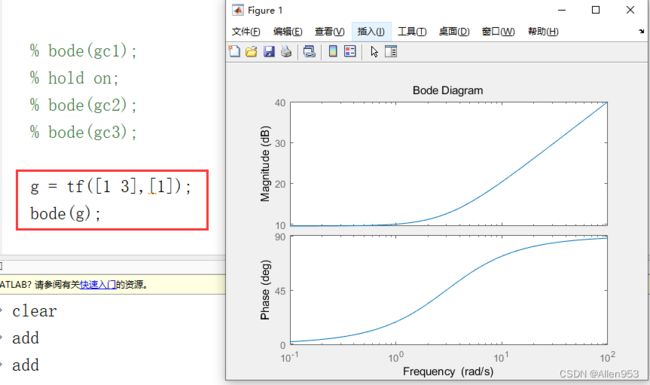
我们随便举个例子，例如S+3这个PD控制器，我们将他的伯德图画出来。
从伯德图的幅频特性可以看到，系统对于高频噪声有着强烈的幅值响应，也就是说当系统遇到高频噪声时，系统的输出幅值会越来越大，最终使系统达到了不稳定的状态。
那么问题就又来了。
为什么PD控制器对高频噪声这么敏感？
从伯德图上我们是看到了PD控制器对高频噪声比较敏感这一特点，但是这是什么原因造成的呢？
为什么PD控制器对高频噪声这么敏感呢？
为什么说系统的幅频曲线要远离0度，相频曲线要远离-180度，系统才能稳定？
介绍如何从相位角度理解稳定性
判断环路稳定的第一步是把闭环打开，基于开环来分析，分析环路从输入到反馈这一条路径的时延（频域是相位延时）。如果开环的相位延时达到了180度，那么再加上负反馈本身的减号（再＋180度），这样参考源就和反馈是叠加了，结果是越来越不稳定（正反馈）。
对于Bode图，我们分析-180度位置的幅值情况，如果小于0db，也就是幅值小于1，就说明正反馈的成分是逐渐衰减的，那么系统就是稳定的。
开环增益K有什么作用？
根轨迹和伯德图分别在时域和频域上包含了系统的全部结构信息，因此改善动态/静态性能等于“操纵”根轨迹和波特图
改变开环增益K是最容易的，但是当系统结构确定的时候，K值的能力范围有限：
（1）体现在根轨迹上，K值只能让根落在属于根轨迹的位置，若指标要求在其他位置，K无能为力
（2）体现在波特图上，K值对相频特性没有影响，对幅频特性只能影响它的上下位置，而不能改变它的“形状”（就是它在哪转折怎么转折）。低频段的高度是由开环比例系数K形成的，K越大，整个曲线平移上去的高度就越高，而我们都知道K越大，系统稳态误差就越小（虽然它不能消除稳态误差）。
这些都是因为，根轨迹、波特图“形状”都是由系统结构决定的，想改变它们，当然要从系统结构入手，系统结构指的就是方块图上积分装置的数量和反馈深度（这自然是废话……不过刚接触控制理论的时候要意识到这些概念也不太容易）。
为什么一个积分环节的伯德图幅频曲线斜率恰恰是一个-20dB/dec？
我们把1/s的伯德图画出来，可以看到斜率确实是-20dB/dec，那么这是为什么呢？
系统的响应跟零点有关系吗？
系统的响应不是由闭环传递函数的极点唯一决定吗？为什么他这个文章这样说？是他说错了吗？还是另有原因？
他这里说的使系统零极点出现在合适的位置应该说的是开环的零点和极点，而非闭环零点和极点。
因为当用根轨迹法分析系统时，分析对象是开环传递函数，我们的控制器往往是通过增加一个合适的零点或极点或者同时增加两者来实现的，也就是说增加的零点和极点都是针对开环传递函数来说的。
而频域法分析系统，分析的也是开环传递函数。所以他这里说的是增加开环零极点，毕竟控制器都是添加在开环系统的前面，也就是在开环下面做的。
那么增加开环零点，能够影响系统响应吗？
答案是可以的。
假设系统开环传递函数为
，
添加的控制器为：
那么：
则系统的闭环传递函数为：
闭环传递函数的特征方程为：
可见，我们通过增加零点使得开环系统下传递函数多了个
而这个多项式同时存在于闭环传递函数的特征方程中，进而影响了闭环传递函数特征方程的解。
所以能够影响系统的响应。
相角裕度和幅值裕度的定义是怎么样的？
幅值裕度h：幅值裕度h的含义是，对于闭环稳定系统，如果系统开环幅频特性再增大h倍，则系统将处于临界稳定状态。
相角裕度γ：相角裕度γ的含义是，对于闭环稳定系统，如果系统开环相频特性再滞后γ度，则系统将处于临界稳定状态。
幅频特性再增大h倍就是说幅频曲线再往上移动h倍，相频特性再滞后γ度就是说相频曲线再往下移动γ度。
相角裕度和幅值裕度能说明什么？
相角裕度越大，说明输出信号与输入信号的实际相位滞后越少。
说明系统的刚性越好，说明系统阻尼系数越大，系统的弹性越小，所以在系统响应过程中，积累的弹性势能越少，最大超调量就越小。
有的系统阻尼系数很小，这样以来弹性就很好，在系统响应（运动）过程中，系统的弹性元件就积累了很多弹性势能，当输出达到期望以后，弹性势能又要释放出来，所以超调量很大。
我们看下面这个图片，如果我们在左边输入一个频率刚好为Wc也就是截止频率，这个时候幅值响应为1.
如果这个弹簧的刚性很好，那么输出基本就能和输入同步，幅值相等，相位滞后也很小。
随着弹簧刚性下降，即阻尼下降，弹簧的弹性慢慢变的好了，使得给质量块1输入一个正弦信号后，质量块二的响应滞后相交变大，越来越大，当刚好滞后180度的时候。相当于质量块一运动到最左端的时候，质量块刚好运动到最右端；同时质量块一运动到最右端的时候，质量快二运动到最左端。这个时候弹簧将得到最大限度的拉伸和压缩。也就是说系统发生了共振，但是由于幅值响应刚好为1，所以使得振幅没有进一步拉大，假设这个时候幅值响应大于1，则震动的幅值将会越来越大，最终将弹簧破环掉。
同时用这个例子来说明上面的超调量，在质量块1往右运动的过程中，弹簧被压缩变形，储备了弹性势能，所以当质量块1运动到最右边的时候，甚至到质量块1又开始往左运动的过程中。由于弹簧一开始被压缩积累了弹性势能，这个时候要伸长释放弹性势能，导致质量块二这个时候依旧是往右运动，由于我们输入的u(t)为期望，这个时候输出x(t)产生了滞后，即便输入减小（质量块1已经往左运动了），输出还在增大（质量块二还在往右运动）。
开环低频增益大，系统的稳态误差小，所以说保证足够的低频开环增益，能够减少稳态误差。
伯德图上能否看出来低频开环增益是多少？如何保证足够的低频开环增益？
伯德图能否看出来系统的固有频率？
从伯德图如何判断是否发生共振？
相角滞后180度，系统一定不稳定吗？
相角滞后180度，说明引发了共振，但是如果这个时候系统的幅值响应为负值，也就是说系统的幅值在衰减，即便引起了共振，系统也是在低幅震动，并不会使得系统不稳定。
共振一定会使得系统不稳定吗？
共振不一定使得系统不稳定，当发生共振时，只要幅值响应不为正值就可以了。如果为正值，则幅值会越来越大，如果不为正值，比如0dB或者0dB以下，则幅值不会无限变大。
伯德图不能同时触碰0dB线和-180度线，这是什么意思？
作者：lenleo
链接：https://www.zhihu.com/question/27347401/answer/630582836
来源：知乎
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。
稳定裕度始终是针对开环系统而言的。开换系统对闭环系统到底有什么影响？
单位负反馈的闭环系统传递函数为：
如果闭环系统不稳定，对于LTI系统而言就是存在极点在右半平面，也可以理解为系统Gain是无穷大（因为不稳定最终会发散）
这就等价于 
，这就和Nyquist曲线里（-1,0）这个特殊点也对应上了。
对于开环系统 
，它的伯德图长这样：
如果伯德图同时触碰了这两条红线，那么系统将处于临界稳定状态吗？是全频率临界稳定状态还是只是在截止频率和穿越频率处（这时截止频率等于穿越频率）临界稳定？
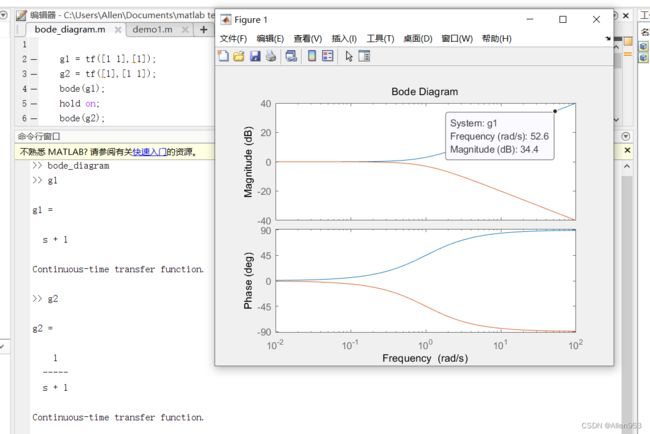
如何判断一个控制器是超前补偿还是滞后补偿？
我们把s+1和1/s+1的伯德图画出来，从下面的图片就能看出来。
s+1是传递函数g1，而g1的伯德图中相频特性是正的，也就是说输出的相位比输入相位要超前。
1/s+1是传递函数g2，而g2的伯德图中相频特性是负的，也就是说输出的相位比输入相位要滞后。
那么当两者组合的时候，如何判断是超前还是滞后呢？我们先来看看滞后补偿器滞后特性是由什么决定的。
我们同时画出来1/s+0.5和1/s+1两个滞后补偿器的伯德图，可以看出，分母中的常数越小，滞后效果越明显，即1/s+0.5的滞后效果更强，同一输入频率下，他的滞后角度更大。
我们同时画出来s+0.5和s+1两个超前补偿器的伯德图，可以看出，分子中的常数越小，超前效果越明显，即s+0.5的超前效果更强，同一输入频率下，他的超前角度更大。
而我们知道，在传递函数表示的系统模型中，数学模型是相乘的关系，但由于伯德图是取的横纵坐标的对数，所以变成了相加的关系，即s+1和1/s+2的伯德图为两者伯德图的纵坐标分别叠加。
那么我们判断一个矫正器是超前补偿器还是滞后补偿器就要看两者叠加滞后是超前的还是滞后的。如果超前补偿器的超前角比滞后补偿器的滞后角大，那么两者结合之后补偿器就是超前的。
如果滞后补偿器的滞后角比超前补偿器的超前角大 ，那么两者结合滞后补偿器就是滞后的。
而同时，我们知道如果s+a中的常数a越小则超前效果越强，即超前角越大。
我们又知道当1/s+b中的常数越小则滞后效果越强，即滞后角越大。
因此我们只需要比较s+a/s+b中常数a和常数b的大小就可以了，哪个常数小，就是哪个占主导地位。例如a
这反映了极点和零点的位置，毕竟当a越小，则零点越大，当b越小则极点越大。
因此也可以直接比较零点和极点。
如果零点更大，则由零点主导，即超前角更大为超前补偿器；
如果极点更大，则由极点主导，即滞后角更大为滞后补偿器。
为什么超前控制器s+a中a越小超前角越大？
还用上一节的图片来分析，我们发现在同一输入频率下s+0.5的超前角比s+1的超前角要大。
那么是什么导致的这个结果呢？
我们可以用simulink把这个s+a的方块图做出来，也就是个典型的PD控制器。
如果a的值越大，则零点越小，这个时候比例环节输出越大，微分环节输出越小，而微分环节是超前校正的，这个时候超前效果就弱了。
如果a的值越小，则零点越大，这个时候微分环节输出越大，比例环节输出越小，这个时候超前效果就变强了。
为什么一阶微分环节可以使得相位超前T秒？
我们先来看一阶微分环节的形式：
然后我们看下面这个方块图表示的系统。
假设我们现在做的是一个速度控制，输入的是个正弦变化的速度期望，输出的也是一个正弦变化的实际速度。
在没有加入超前补偿器的情况下，输出可能会滞后输入一个相角。
但是加入了超前补偿器（一阶微分环节）之后，我们发现什么变化了呢？
就是输入到G(s)的信号发生了变化。原本我们输入一个期望的v，是直接输入到系统G(s)里面的。
现在是输入一个期望的v之后，先是做了个乘法运算。
变成了下面这种形式，原本输入的是现在的期望速度v进去的，结果他加了个对未来的预测——用当前加速度a乘上时间常数T，也就是未来T时间里面的速度变化量，所以得到了未来T时刻的速度期望，这样再输入G(s)的时候，输入的速度期望实际上是未来T时刻的时候的速度期望，而非当前的速度期望。所以输入超前了，当输出滞后相角一定的时候，输入超前带来的是输出比原先滞后的更少或者也超前了。
我们可以看下面这个例子，原本输入的是蓝色信号，通过系统G(s)之后，输出的是红色信号，刚好滞后了pi/3的相角。
而加入了超前补偿器之后，输入信号还是蓝色，但是经过超前补偿器之后变成了橙色（因为提前输入了未来的信号），所以经过系统G(s)之后，虽然还是滞后了pi/3的相角，但现在变成了紫色信号。
也就是说同样蓝色信号输入，原本输出红色信号的，现在输出紫色信号了，滞后的相角变小了，这就是超前补偿器使得相角超前的作用带来的效果。
为什么一阶惯性环节的输出比输入延迟时间常数T时间？
我们知道一阶惯性环节的传递函数为
输入信号在经过一阶惯性环节之后会滞后T秒的时间，我们可以在matlab里面搭建一个简单的模型进行实验。