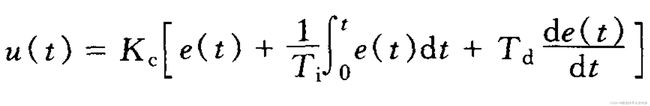计算机物联网控制｜5.5常规控制方案 5.6先进控制方案

11.16日课堂作业

1.已知模拟PID算式为

试推导差分增量算式。                                                                                                                        

2.PID参数Kc、Ti、Td对系统动态特性和稳态特性有何影响？

目录

11.16日课堂作业

5.5常规控制方案Routine Control Scheme

5.5-1串级控制系统

1.串级控制系统基本概念

2.双回路串级控制系统

3.串级控制系统在每个采样周期的计算顺序 

4.串级控制系统的控制方式

4.1异步采样控制

4.2同步采样控制

5.串级控制系统的应用目的

5.5-2前馈控制系统

1.主要特点 

2.典型的前馈-反馈控制系统

3.前馈-反馈控制算法的流程

5.5-3纯滞后补偿控制系统

1.史密斯Smith纯滞后补偿器基本思想

2.史密斯(Smith)纯滞后补偿器

3.史密斯(Smith)纯滞后补偿系统实施

3.1纯滞后的表示

3.2史密斯预估控制系统的计算顺序

3.3史密斯预估控制器仿真实例​编辑

4.史密斯(Smith)预估器的不足

4.1改进算法

5.6先进控制方案

5.6-1预测控制

1.预测控制由来

2.预测控制特点

3.预测控制基本原理

3.模型输出预测

​4.滚动优化

4.1优化目的

4.2优化过程 

5.反馈校正

6.常见预测控制方案

7.预测控制发展

8.商品化预测控制软件

5.6-2专家系统 

1.专家系统概述

2.专家系统应用分类 

3.专家系统特点

4.专家系统结构 

5.专家系统建造步骤

---

5.5常规控制方案Routine Control Scheme

串级控制系统

前馈控制系统

纯滞后补偿控制系统

5.5-1串级控制系统

1.串级控制系统基本概念

主调节回路要保证控制精度，主调节器一般采用PID控制器。

副调节回路克服主要干扰，系统中起“粗调”作用，副调节器一般采用P或PI控制器。

2.双回路串级控制系统

3.串级控制系统在每个采样周期的计算顺序 

        ·采样并获得当前输出采样值；

        ·计算主回路的偏差 ；

        ·计算主回路PID控制器的输出；

        ·计算副回路偏差；

        ·计算副回路PID控制器的输出；

        ·输出到被控对象。

主调节器和副调节器的选型很重要；

计算机编程大都使用增量式编程方法。

4.串级控制系统的控制方式

4.1异步采样控制

即主回路的采样控制周期  是副回路采样控制周期  的整数倍。

4.2同步采样控制

即主、副回路的采样周期相同，但因副对象响应速度较快，故应以副回路为准。

5.串级控制系统的应用目的

——用于抑制系统的主要干扰

——用于克服对象的纯滞后

——用于减少对象的非线性影响

例：反应釜的单回路控制、串级控制

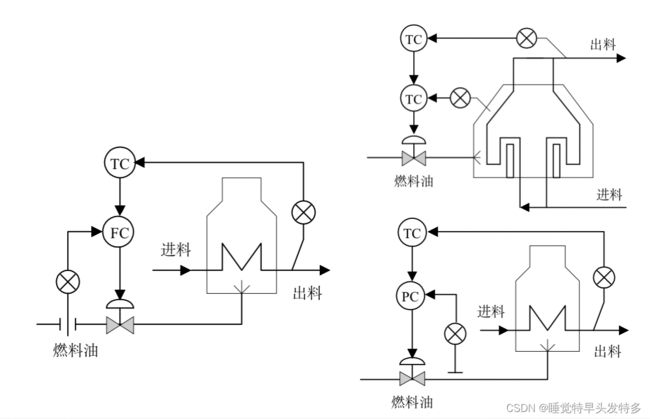
例：加热炉的串级控制

5.5-2前馈控制系统

前馈控制系统的基本思想：不变性原理；

1.主要特点 

——是一个开环系统

——应用前提是扰动可测

——只能针对某一特定的干扰实施控制

较少单独使用，一般结合反馈控制，构成前馈-反馈(Feedforword-Feedback)控制。

2.典型的前馈-反馈控制系统

3.前馈-反馈控制算法的流程

——计算反馈控制的偏差e(k)；

——计算反馈控制器(PID)的输出；

——计算前馈控制器的输出；

——计算前馈-反馈调节器的输出。

前馈：快速、对具体干扰；

反馈：慢速、准确、对整个系统。

前馈-反馈控制系统：可以取得较好的控制效果，实际中也常采用前馈-串级控制。

例：换热器前馈控制系统

例：精馏塔前馈-反馈控制系统

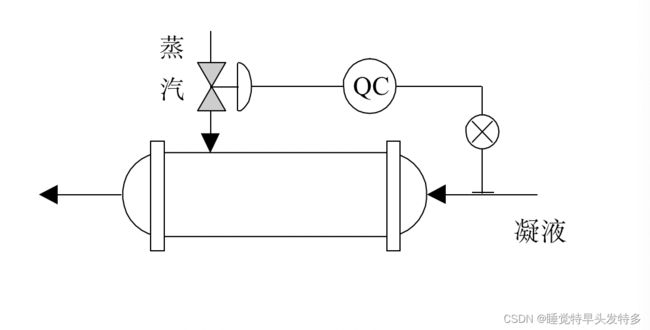
5.5-3纯滞后补偿控制系统

在工业控制系统中，由于物料或能量的传输延迟，许多被控对象具有纯滞后。

由于纯滞后的存在，被控量不能及时反映系统变化，即使测量信号已到达调节器，执行机构迅速动作，也需要纯滞后时候后才能影响到被控量。

具有纯滞后的对象被公认为过程控制的难点之一。

1.史密斯Smith纯滞后补偿器基本思想

——建立过程的动态特性的模型；

——将模型加入到反馈系统中，有延迟的一部分用于抵消被延迟了的被控量；

——无延迟部分反映到调节器，让调节器提前动作，从而可明显地减少超调量和加快调节过程。

预估是纯滞后控制中的基本方法。

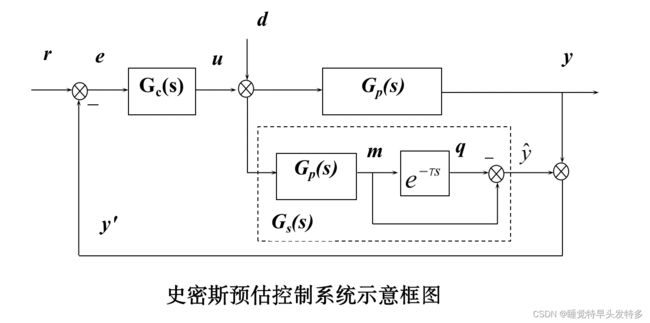
2.史密斯(Smith)纯滞后补偿器

图中虚框即为史密斯预估器，其等效传递函数为:

闭环传递函数为:

3.史密斯(Smith)纯滞后补偿系统实施

3.1纯滞后的表示

——设采样周期为T，则由于纯滞后t的存在，信号要延迟N个周期：N=t/T；

——内存中设N个单元存放信号m(k)的历史数据；

——第N号单元里的内容即为m(k)滞后N个采样周期后的信号q(q=m(k-N))。

3.2史密斯预估控制系统的计算顺序

——计算反馈回路的偏差e(k)：

e(k)=r(k)-y'(k)=r(k)-y(k)-(k)

——控制器的输出u(k):

u(k)=u(k-1)+u(k)

——史密斯预估器的输出：

=m(k)-m(k-N)

前面式中的m(k)根据被控对象的数学模型的差分形式和控制器的输出u(k)计算得到。

教材中给出了对象为一阶加纯滞后的史密斯(Smith)预估器控制算式。

3.3史密斯预估控制器仿真实例

4.史密斯(Smith)预估器的不足

——对系统受到的负荷干扰无补偿作用；

——控制效果严重依赖于对象的动态模型精度，特别是纯滞后时间。

4.1改进算法

加入自适应功能等。

多回路控制也可与PID算法结合应用

5.6先进控制方案

5.6-1预测控制

1.预测控制由来

工业过程的特点：多变量、非线性、强耦合、不确定性、约束。

现代控制理论与方法：精确的数学模型、最优的性能指标 、系统而精确的设计方法。

工业过程对控制的要求：高质量的控制性能 、对模型要求不高、实现方便  、强鲁棒性。

2.预测控制特点

一类用计算实现的最优控制算法；

建模方便，不需要深入了解过程内部机理；

非最小化描述的离散卷积模型，有利于提高提高系统的鲁棒性；

滚动优化模型，较好的动态控制效果；

简单实用的模型校正法，较强的鲁棒性；

可推广应用于带约束、大纯滞后、非最小相位、多输入多输出、非线形等过程。

3.预测控制基本原理

3.模型输出预测

4.滚动优化

4.1优化目的

通过使某一性能指标J极小化，以确定未来的控制作用u(k+j|k)。指标J希望模型预测输出尽可能趋近于参考轨迹。

4.2优化过程 

滚动优化在线反复进行。优化目标只关心预测时域内的动态性能，而且只将u(k|k)施加于被控过程。

5.反馈校正

每到一个新的采样时刻，都要通过实际测到的输出信息对基于模型的预测输出进行修正，然后再进行新的优化。不断根据系统的实际输出对预测输出值作出修正使滚动优化不但基于模型，而且利用了反馈信息，构成闭环优化。

6.常见预测控制方案

动态矩阵控制 (Cutler et al, 1980)     （Dynamic Matrix Control, DMC）

模型算法控制(Richalet et al, 1978)     （Model Algorithm Control, MAC）

广义预测控制(Clarke et al, 1987)     （Generalized Predictive Control, GPC）

预测函数控制(Adersa et al, 1987)     （Predictive Functional Control, PFC）

7.预测控制发展

单输入输出(SISO)——>多输入输出(MIMO)

无约束——>有约束

输入输出方系统——>非方系统

线性——>非线性

常规预测控制——>鲁棒预测控制

8.商品化预测控制软件

5.6-2专家系统 

1.专家系统概述

2.专家系统应用分类 

3.专家系统特点

启发性 透明性 灵活性

4.专家系统结构 

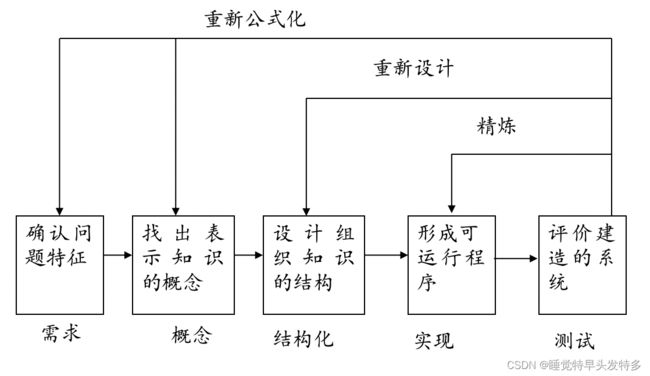
5.专家系统建造步骤

——确认

——概念化

——形式化

——实现

——测试