数学建模常见算法-聚类算法

  数学建模中常采用聚类算法对给定的数据进行分类，然后结合题目条件对不同的类别进行分析。今天主要介绍聚类算法是模糊C-均值聚类算法(FCM)。

        数学建模中常采用聚类算法对给定的数据进行分类，然后结合题目条件对不同的类别进行分析。今天主要介绍聚类算法是模糊C-均值聚类算法(FCM)。

1 FCM原理

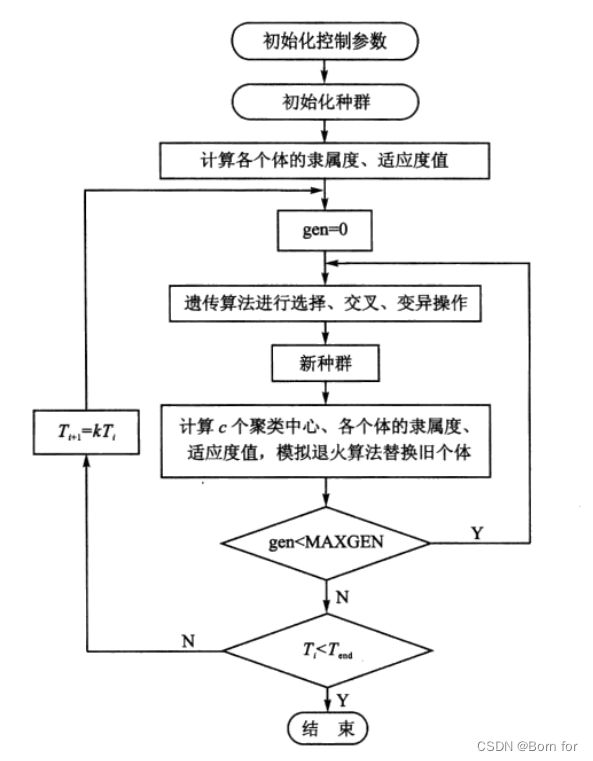
             由于FCM是一种局部搜索算法，且对聚类中心的初值十分敏感，如果处置选择不当，它会收敛到局部极小点。故可采用模拟退火基因遗传算法进行优化。算法流程图如下图所示。

2、程序

% 遗传算法改进的模糊C-均值聚类MATLAB源码
function [BESTX,BESTY,ALLX,ALLY]=GAFCM(K,N,Pm,LB,UB,D,c,m)
%% 此函数实现遗传算法，用于模糊C－均值聚类
%% 输入参数列表
% K        迭代次数
% N        种群规模，要求是偶数
% Pm       变异概率
% LB       决策变量的下界，M×1的向量
% UB       决策变量的上界，M×1的向量
% D        原始样本数据，n×p的矩阵
% c        分类个数
% m        模糊C均值聚类数学模型中的指数
%% 输出参数列表
% BESTX    K×1细胞结构，每一个元素是M×1向量，记录每一代的最优个体
% BESTY    K×1矩阵，记录每一代的最优个体的评价函数值
% ALLX     K×1细胞结构，每一个元素是M×N矩阵，记录全部个体
% ALLY     K×N矩阵，记录全部个体的评价函数值
%% 第一步：
M=length(LB);%决策变量的个数
%种群初始化，每一列是一个样本
farm=zeros(M,N);
for i=1:M
    x=unifrnd(LB(i),UB(i),1,N);
    farm(i,:)=x;
end
%输出变量初始化
ALLX=cell(K,1);%细胞结构，每一个元素是M×N矩阵，记录每一代的个体
ALLY=zeros(K,N);%K×N矩阵，记录每一代评价函数值
BESTX=cell(K,1);%细胞结构，每一个元素是M×1向量，记录每一代的最优个体
BESTY=zeros(K,1);%K×1矩阵，记录每一代的最优个体的评价函数值
k=1;%迭代计数器初始化
%% 第二步：迭代过程
while k<=K
%% 以下是交叉过程
    newfarm=zeros(M,2*N);
    Ser=randperm(N);%两两随机配对的配对表
    A=farm(:,Ser(1));
    B=farm(:,Ser(2));
    P0=unidrnd(M-1);
    a=[A(1:P0,:);B((P0+1):end,:)];%产生子代a
    b=[B(1:P0,:);A((P0+1):end,:)];%产生子代b
    newfarm(:,2*N-1)=a;%加入子代种群
    newfarm(:,2*N)=b;    
    for i=1:(N-1)
        A=farm(:,Ser(i));
        B=farm(:,Ser(i+1));
        P0=unidrnd(M-1);
        a=[A(1:P0,:);B((P0+1):end,:)];
        b=[B(1:P0,:);A((P0+1):end,:)];
        newfarm(:,2*i-1)=a;
        newfarm(:,2*i)=b;
    end    
    FARM=[farm,newfarm];    
%% 选择复制
    SER=randperm(3*N);
    FITNESS=zeros(1,3*N);
    fitness=zeros(1,N);
    for i=1:(3*N)
        Beta=FARM(:,i);
        FITNESS(i)=FIT(Beta,D,c,m);
    end    
    for i=1:N
        f1=FITNESS(SER(3*i-2));
        f2=FITNESS(SER(3*i-1));
        f3=FITNESS(SER(3*i));
        if f1<=f2&&f1<=f3
            farm(:,i)=FARM(:,SER(3*i-2));
            fitness(:,i)=FITNESS(:,SER(3*i-2));
        elseif f2<=f1&&f2<=f3
            farm(:,i)=FARM(:,SER(3*i-1));
            fitness(:,i)=FITNESS(:,SER(3*i-1));
        else
            farm(:,i)=FARM(:,SER(3*i));
            fitness(:,i)=FITNESS(:,SER(3*i));
        end
    end    
    %% 记录最佳个体和收敛曲线
    X=farm;
    Y=fitness;
    ALLX{k}=X;
    ALLY(k,:)=Y;
    minY=min(Y);
    pos=find(Y==minY);
    BESTX{k}=X(:,pos(1));
    BESTY(k)=minY;    
    %% 变异
    for i=1:N
        if Pm>rand&&pos(1)~=i
            AA=farm(:,i);
            BB=GaussMutation(AA,LB,UB);
            farm(:,i)=BB;
        end
    end
    disp(k);
    k=k+1;
end
%% 绘图
BESTY2=BESTY;
BESTX2=BESTX;
for k=1:K
    TempY=BESTY(1:k);
    minTempY=min(TempY);
    posY=find(TempY==minTempY);
    BESTY2(k)=minTempY;
    BESTX2{k}=BESTX{posY(1)};
end
BESTY=BESTY2;
BESTX=BESTX2;
plot(BESTY,'-ko','MarkerEdgeColor','k','MarkerFaceColor','k','MarkerSize',2)
ylabel('函数值')
xlabel('迭代次数')
grid on