s2p文件取实部虚部matlab,一种基于时域建模与频域对称的磁共振信号消噪方法与流程...
本发明属于核磁共振数据处理领域,具体地来讲为一种基于时域建模与频域对称的磁共振信号消噪方法。
背景技术:
自80年代末期开始,核磁共振地下水探测方法(Magnetic Resonance Sounding,MRS)逐渐发展成为最具竞争力的地球物理方法之一。其特点是在不破坏地表的前提下,就可以直接确定含水量和含水层深度等信息。但是,磁共振方法探测到的地下水信号非常微弱,量级通常只有几百nV,因此需要仪器具有极高的灵敏度,导致仪器在探测过程中容易受到来自外界环境的噪声干扰。常见噪声干扰来源主要有由雷电等自然干扰源产生的尖峰噪声,由电力线等人工装置产生的工频噪声和由仪器电路等产生的随机噪声。为了准确提取核磁共振信号,提高后期反演解释结果的精确性,必须采用合理有效的数据处理方法消除原采集数据中的噪声。
专利CN104777442B公开了“一种核磁共振测深FID信号噪声抑制方法”,对磁共振测深系统检测到的信号进行频谱分析,利用归一化正交检测技术将检测到的信号分解为同向分量X、正交分量Y,并进行硬件滤波处理得到低频的FID信号;对采集数据采用非线性能量算子算法分别剔除FID信号中X、Y分量的尖峰噪声;基于主成分分析方法对X、Y分量分别进行初步的信噪分离;基于经验模态分解方法对PCA处理后的X、Y分量进一步分解提取信号趋势项;对EMD处理后的X、Y分量分别叠加求平均后获得e指数曲线。该方法摒弃了传统滤波手段容易对信号成分造成损失等问题,实现了对核磁共振测深FID信号中包含各种复杂噪声的有效抑制,但是计算过程复杂,数据计算量大,工作时间长,效率较低。
专利CN107045149B公开了“一种基于双奇异值分解的全波核磁共振信号噪声滤除方法”,利用地面核磁共振地下水探测仪器采集一组观测MRS含噪数据;对数据进行以拉莫尔频率为中心的带阻滤波,实现初步信噪分离;进行两次奇异值分解,用观测MRS含噪数据减去重构出的噪声数据,获得想要提取的MRS信号。该方法针对单通道采集的全波MRS数据,可以去除工频谐波干扰和随机噪声的影响,提高信噪比。但是与最优降噪效果对应的奇异值数目,往往只能依赖经验选取,使消噪效果出现不确定性。
蒋川东在Near Surface Geophysics[2011,9(5),459-468]上发表的论文“Statistical stacking and adaptive notch filter to remove high-level electromagnetic noise from MRS measurements”中对所有单次采集的信号进行叠加处理,并采用自适应陷波器消除工频谐波噪声。但是当噪声来源复杂多变时,消噪效率会降低,且在拉莫尔频率附近出现失真的现象。
技术实现要素:
本发明所要解决的技术问题在于提供一种基于时域建模与频域对称的磁共振信号消噪方法,解决消噪效率低,信号失真的问题。
本发明是这样实现的,
一种基于时域建模与频域对称的磁共振信号消噪方法,该方法包括:
A、录入核磁共振地下水探测仪采集的主通道与参考通道数据Ns组,主通道的每组数据中含有按时间顺序采集的空采噪声N1P(k)和含噪声的核磁共振信号S2P(k),参考通道的每组数据中只含有同步采集的噪声数据N1R(k)和噪声数据N2R(k),k为离散样本点,Ns为叠加次数,叠加次数是2的整数次幂;
B、分别对每组含噪声的核磁共振数据S2P(k)中工频谐波噪声进行时域建模,并从原始数据中减去建立的噪声模型,得到Ns组消除工频谐波干扰的核磁共振信号数据;
C、将步骤B中得到的Ns组消除工频谐波干扰的核磁共振信号数据进行叠加平均处理,得到一组核磁共振信号数据S(k);
D、利用核磁共振信号的频域对称性,消除残余工频噪声和高斯白噪声,重构核磁共振信号,得到最终的消噪数据。
进一步地,步骤B中的时域建模包括:
对主通道数据S2P(k)中远离拉莫尔频率fL附近的工频噪声成分建立数学模型hp(k);
根据空采噪声在主通道与参考通道之间模型参数的转换关系,确定核磁共振信号S2P(k)拉莫尔频率fL附近的工频噪声数学模型hL(k);
确定工频噪声H(k)=hp(k)+hL(k)。
进一步地,步骤B中的时域建模的具体步骤为:
B1、对第一组含噪声的核磁共振信号数据,确定拉莫尔频率fL附近工频谐波干扰频率对于电力线基频的整数倍为
B2、对主通道数据S2P(k)中远离拉莫尔频率fL附近的工频噪声成分建立数学模型
其中,fs为采样频率,f0为电力线基频,m为基频f0的正整数倍,用于确定每个工频噪声成分的位置,m∈[1,100],αm和βm为待定参数;
B3、确定电力线基频值f0;
B4、将f0、fs、k代入步骤B2工频噪声数学模型,取m=1,2,...,100且m≠ml和mr,分别采用最小二乘法,以步骤B2中的工频噪声模型拟合核磁共振数据S2P(k),得到参数αm和参数βm,m=1,2,...,100且m≠ml和mr;
B5、根据空采噪声在主通道与参考通道之间模型参数的转换关系,确定核磁共振信号S2P(k)拉莫尔频率fL附近的工频噪声数学模型:
B6、工频噪声H(k)=hp(k)+hL(k),由核磁共振原始数据S2P(k)减去工频噪声H(k),得到第一组去工频谐波后的核磁共振信号,记为S1;
B7、针对第2~Ns组数据,重复步骤B4~B6,得到去工频谐波后的核磁共振信号S2,S3,...,SNs。
进一步地,步骤B3确定电力线基频值f0包括:取m为m∈[1,100]且m≠ml和mr的一个固定值,当fi=49.9+0.001*i,i=0,1,2,...,200时,分别采用最小二乘法,以远离拉莫尔频率fL附近的工频噪声成分建立数学模型拟合核磁共振数据S2P(k),得到拟合残差r0(k),r1(k),...,r200(k);取ri(k)=min{r0(k),r1(k),...,r200(k)},此时i值对应的fi,为采集数据S2P(k)时刻的电力线基频值f0。
进一步地,步骤B5根据空采噪声在主通道与参考通道之间模型参数的转换关系,确定核磁共振信号S2P(k)拉莫尔频率fL附近的工频噪声数学模型其具体操作步骤为:
B5a,取m=ml和mr,采用最小二乘法,以步骤B2中的工频噪声模型分别拟合噪声数据N1P(k)、N1R(k)和N2R(k),得到参数[α1Pl,β1Pl,α1Pr,β1Pr,α1Rl,β1Rl,α1Rr,β1Rr,α2Rl,β2Rl,α2Rr,β2Rr],根据公式计算得到参数
B5b,计算空采噪声数据参数转换关系:
B5c,利用空采噪声数据参数转换关系和与磁共振信号同步采集的参考道数据工频噪声模型参数,计算得到核磁共振信号S2P(k)拉莫尔频率fL附近的工频噪声数学模型参数Al=μl*A2Rl,Ar=μr*A2Rr,则核磁共振信号S2P(k)拉莫尔频率fL附近的工频噪声数学模型
进一步地,所述步骤D中的频域对称法的具体步骤为:
D1、对步骤C中叠加平均处理后的核磁共振信号S(k)进行傅里叶变换,记频域出现噪声尖峰处的频率为x1,x2,x3,...;在频域解调信号,选择以ω=fL为中心的频带,将幅度缩放2倍,并将该频谱移动到以ω=0为中心处,再进行傅里叶反变换,得到的时域数据的实部SR(k)为受噪声干扰的磁共振包络信号,时域数据的虚部SI(k)通过计算转换为磁共振包络信号中残余噪声;
D2、对时域数据的实部SR(k)和时域数据的虚部SI(k)分别进行傅里叶变换,得到频谱FR(ω)和频谱FI(ω),在频谱FI(ω)中,对ω=fL-x1,fL-x2,fL-x3,...处的幅度乘因子-1得到频谱FT(ω),转换后的频谱FC(ω)=FR(ω)-FT(ω);
D3、对频谱FC(ω)在频域进行调制,将频谱幅度缩放并将频谱移动到以ω=fL为中心处,得到修正后的磁共振信号频谱F(ω),再对F(ω)进行傅里叶反变换,得到消减残余工频噪声和高斯白噪声后的较为精确的核磁共振信号序列。
本发明与现有技术相比,有益效果在于:
本发明根据核磁共振信号和噪声呈现的数学特征,分别从时域和频域两个方面提出了核磁共振信号中噪声的消除方法。首先,根据工频噪声持续时间长,是一系列固定在电力线基频整数倍处的正弦波的特点,对噪声建模,并利用多通道仪器采集核磁共振信号和噪声数据,将参考通道中的工频噪声转换为主通道中的工频噪声,避免了在消除拉莫尔频率附近工频噪声时产生信号失真。随后,利用核磁共振信号和噪声成分经过傅里叶变换后在频域呈现的不同对称性,进一步消除残余工频噪声和高斯白噪声。本方法的噪声消除效果具有确定性,能够显著增强信噪比,并提高后续反演解释得到水文地质参数的准确性。
附图说明
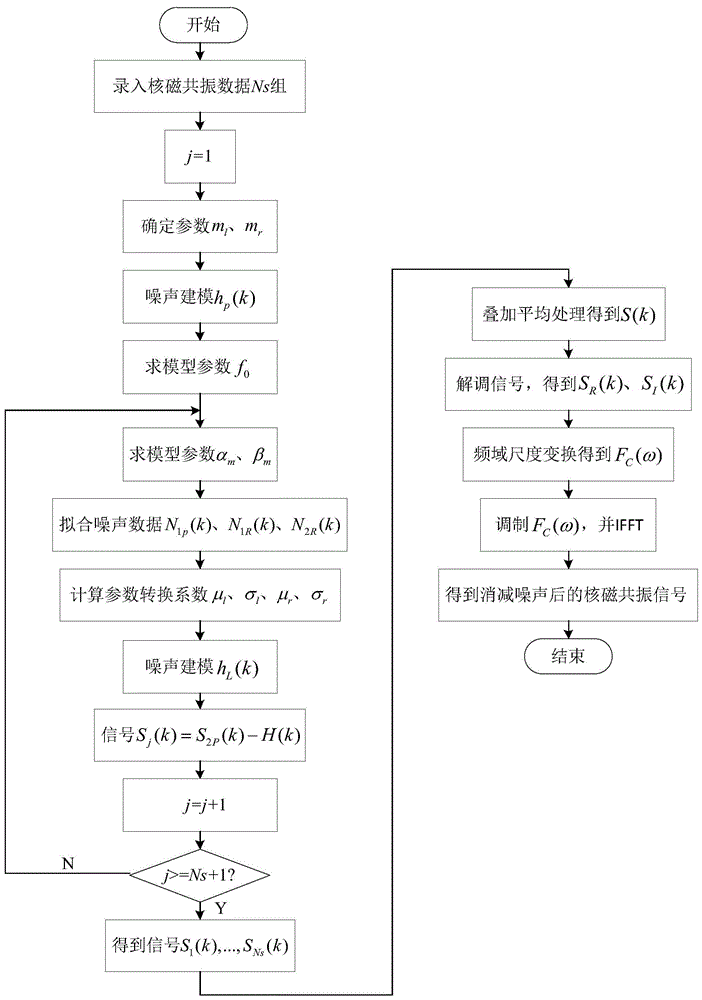
图1为基于时域建模与频域对称的磁共振信号消噪方法流程图;
图2为第1组含工频噪声和随机噪声的核磁共振信号时域图(A)和频域图(B);
图3为确定基频f0时的拟合残差;
图4为远离拉莫尔频率处工频噪声成分建模的时域图(A)和频域图(B);
图5为主通道与参考道之间工频噪声模型转换示意图;
图6为拉莫尔频率邻近工频噪声成分建模的时域图(A)和频域图(B);
图7为消除时域建模噪声后的磁共振信号时域图(A)和频域图(B);
图8为核磁共振信号和2500Hz处噪声成分的时域图(A)和频域图(B);
图9为核磁共振信号和2500Hz处噪声成分解调后的时域图(A)和频域图(B);
图10为信号解调后时域虚部成分SI(k)的时域图(A)和频域图(B);
图11为频谱变换后得到的时域实部成分SR(k)中噪声的时域图(A)和频域图(B);
图12为消除噪声成分后得到的转换频谱FC(ω)(A)和其经傅里叶反变换后得到的核磁共振包络信号(B);
图13为调制后得到的核磁共振信号频谱图(A)和傅里叶反变换后得到的核磁共振全波信号图(B);
图14为利用频域对称法进一步消除残余噪声后的核磁共振信号时域图(A)和频域图(B)。
具体实施方式
为了使本发明的目的、技术方案及优点更加清楚明白,以下结合实施例,对本发明进行进一步详细说明。应当理解,此处所描述的具体实施例仅仅用以解释本发明,并不用于限定本发明。
图1是基于时域建模与频域对称的磁共振信号消噪方法流程图。首先根据工频噪声特点对噪声成分进行建模,消除大部分工频噪声,然后利用噪声在频域的对称性构建噪声成分,进一步消除残余噪声。
参见图1所示,下面是基于时域建模与频域对称的磁共振信号消噪方法的具体步骤:
A、录入核磁共振地下水探测仪采集的主通道与参考通道数据Ns组,主通道的每组数据中含有按时间顺序采集的空采噪声N1P(k)和含噪声的核磁共振信号S2P(k),参考通道的每组数据中只含有同步采集的噪声数据N1R(k)和N2R(k),k为离散样本点,Ns为叠加次数,由采集地点的具体情况确定,是2的整数次幂;
B、分别对每组含噪声的核磁共振数据S2P(k)中工频谐波噪声进行时域建模,并从原始数据中减去建立的噪声模型,得到Ns组消除工频谐波干扰的核磁共振信号数据;
C、将步骤B中得到的Ns组数据进行叠加平均处理,得到一组核磁共振信号数据S(k);
D、利用核磁共振信号的频域对称性,消除残余工频噪声和高斯白噪声,重构核磁共振信号,得到最终的消噪数据。
所述步骤B中的时域建模算法的具体步骤为:
B1、对第一组含噪声的核磁共振信号数据,确定拉莫尔频率fL附近工频谐波干扰频率对于电力线基频的整数倍为(其中为向下取整,为向上取整);
B2、对主通道数据S2P(k)中远离拉莫尔频率fL附近的工频噪声成分建立数学模型(不包括拉莫尔频率相邻两个工频噪声频率处的噪声)
其中,fs为采样频率,f0为电力线基频,m为基频f0的正整数倍,用于确定每个工频噪声成分的位置,m∈[1,100]。αm和βm为待定参数;
B3、确定电力线基频值。取m为m∈[1,100]且m≠ml和mr的一个固定值,当fi=49.9+0.001*i,i=0,1,2,...,200时,分别采用最小二乘法,以步骤b的工频噪声数学模型拟合核磁共振数据S2P(k),得到拟合残差r0(k),r1(k),...,r200(k)。取ri(k)=min{r0(k),r1(k),...,r200(k)},此时i值对应的fi,即为采集数据S2P(k)时刻的电力线基频值f0;
B4、将f0、fs、k代入步骤B2的工频噪声数学模型,取m=1,2,...,100且m≠ml和mr,分别采用最小二乘法,以步骤B2的工频噪声模型拟合核磁共振数据S2P(k),得到参数αm和βm,m=1,2,...,100且m≠ml和mr;
B5、根据空采噪声在主通道与参考通道之间模型参数的转换关系,确定核磁共振信号S2P(k)拉莫尔频率fL附近的工频噪声数学模型(只包括拉莫尔频率相邻两个工频噪声频率处的噪声的工频噪声模型),其具体操作步骤为:
B5a,取m=ml和mr,采用最小二乘法,以步骤B2中的工频噪声数学模型分别拟合噪声数据N1P(k)、N1R(k)和N2R(k),得到参数[α1Pl,β1Pl,α1Pr,β1Pr,α1Rl,β1Rl,α1Rr,β1Rr,α2Rl,β2Rl,α2Rr,β2Rr]。根据公式计算得到参数
B5b,计算空采噪声数据参数转换关系,
B5c,利用空采噪声数据参数转换关系和与磁共振信号同步采集的参考道数据工频噪声模型参数,计算得到核磁共振信号S2P(k)拉莫尔频率fL附近的工频噪声数学模型参数Al=μl*A2Rl,Ar=μr*A2Rr,则核磁共振信号S2P(k)拉莫尔频率fL附近的工频噪声数学模型
B6、工频噪声H(k)=hp(k)+hL(k),由核磁共振原始数据S2P(k)减去工频噪声H(k),得到第一组去工频谐波后的核磁共振信号,记为S1;
B7、针对第2~Ns组数据,重复步骤B4~B6,得到去工频谐波后的核磁共振信号S2,S3,...,SNs。
所述步骤D中的频域对称法的具体步骤为:
D1、对步骤C中叠加平均处理后的核磁共振信号S(k)进行傅里叶变换,记频域出现噪声尖峰处的频率为x1,x2,x3,...。在频域解调信号,选择以ω=fL为中心的频带,将幅度缩放2倍,并将该频谱移动到以ω=0为中心处,再进行傅里叶反变换,得到的时域数据的实部SR(k)为受噪声干扰的磁共振包络信号,时域数据的虚部SI(k)可通过计算转换为磁共振包络信号中残余噪声;
D2、对时域数据的实部SR(k)和时域数据的虚部SI(k)分别进行傅里叶变换,得到频谱FR(ω)和FI(ω)。在FI(ω)频谱中,对ω=fL-x1,fL-x2,fL-x3,...处的幅度乘因子-1得到频谱FT(ω),转换后的频谱FC(ω)=FR(ω)-FT(ω);
D3、对频谱FC(ω)在频域进行调制,将频谱幅度缩放并将频谱移动到以ω=fL为中心处,得到修正后的磁共振信号频谱F(ω),再对F(ω)进行傅里叶反变换,得到消减了残余工频噪声和高斯白噪声后的较为精确的核磁共振信号序列。
应用实例:
以吉林省长春市烧锅镇核磁共振地下水探测为例:根据当地地磁场强度计算得到拉莫尔频率为2326Hz,数据序列长度为25600,采样频率为25000Hz。在matlab环境下采用基于时域建模与频域对称的磁共振信号消噪方法处理实测数据。具体步骤如下:
1.录入核磁共振地下水探测仪采集的主通道与参考通道数据64组,主通道的每组数据中含有按时间顺序采集的空采噪声N1P(k)和含噪声的核磁共振信号S2P(k),参考通道的每组数据中只含有同步采集的噪声数据N1R(k)和N2R(k),k为离散样本点。其中第一组数据中含噪声的核磁共振信号S2P(k)如图2所示(图2A为时域图,图2B为频域图)。
2.确定拉莫尔频率fL附近工频谐波干扰频率对于电力线基频的整数倍为
3.对主通道数据S2P(k)中远离拉莫尔频率fL附近的工频噪声成分建立数学模型
其中,fs为采样频率25000Hz,f0为电力线基频,m为基频f0的正整数倍,用于确定每个工频噪声成分的位置,m∈[1,100]。αm和βm为待定参数。
4.确定电力线基频值。取m为m∈[1,100]且m≠ml和mr的一个固定值,当fi=49.9+0.001*i,i=0,1,2,...,200时,分别采用最小二乘法,以工频噪声数学模型拟合核磁共振数据S2P(k),得到拟合残差r0(k),r1(k),...,r200(k),拟合残差随基频值变化趋势如图3所示,由图3可以看出,在fi=50.012Hz处拟合残差取得最小值,因此采集数据S2P(k)时刻的电力线基频值f0=50.012Hz。
5.将f0=50.012Hz、fs=25000Hz、k=1,2,...,25600代入工频噪声数学模型,取m=1,2,...,100且m≠ml和mr,分别采用最小二乘法,以工频噪声模型拟合核磁共振数据S2P(k),得到参数αm和βm,m=1,2,...,100且m≠ml和mr。图4所示为建立的工频噪声模型hp(k)的时域图(图4A)和频域图(图4B)。
6.由于空采噪声和核磁共振信号采集时间极短,在这段时间内主通道与参考通道的噪声之间的相关性可以认定为不变。利用无信号段的数据估算核磁共振信号中的噪声,能够避免信号对噪声估计产生的影响,从而在消去噪声时不会产生信号失真,其原理图如图5所示。取m=ml和mr,采用最小二乘法,以步骤3中工频噪声模型分别拟合噪声数据N1P(k)、N1R(k)和N2R(k),得到参数[α1Pl,β1Pl,α1Pr,β1Pr,α1Rl,β1Rl,α1Rr,β1Rr,α2Rl,β2Rl,α2Rr,β2Rr]。根据公式计算得到参数
7.计算空采噪声数据参数转换关系,
8.利用空采噪声数据参数转换关系和与磁共振信号同步采集的参考道数据工频噪声模型参数,计算得到核磁共振信号S2P(k)拉莫尔频率fL附近的工频噪声数学模型参数Al=μl*A2Rl,Ar=μr*A2Rr,则核磁共振信号S2P(k)拉莫尔频率fL邻近的工频噪声数学模型
图6为hL(k)的时域图(图6A)和频域图(图6B)。
9.工频噪声H(k)=hp(k)+hL(k),由核磁共振原始数据S2P(k)减去工频噪声H(k),得到第一组去工频谐波后的核磁共振信号,记为S1。其时域图(图7A)和频域图(图7B)如图7所示。
10.针对第2~64组数据,重复步骤5~9,得到去工频谐波后的核磁共振信号S2,S3,...,SNs。
11.将步骤10中得到的64组数据进行叠加平均处理,得到一组核磁共振信号数据S(k);
12.对步骤11中叠加平均处理后的核磁共振信号S(k)进行傅里叶变换,为了方便说明,截取信号频率2326Hz和频率为2500Hz的噪声成分的频谱,图8所示为信号和该噪声成分的时域图(8A)和频域图(8B),频域图中实线曲线为傅里叶变换后的偶对称实部曲线,虚线曲线为奇对称虚部曲线。在频域解调信号,选择以ω=2326Hz为中心的频带,将幅度缩放2倍,并将该频谱移动到以ω=0Hz为中心处,再进行傅里叶反变换,解调后信号和噪声的时域图(图9A)和频域图(图9B)如图9所示,图9A中深黑色曲线为实部曲线,浅灰色曲线为虚部曲线。时域数据的实部SR(k)为受噪声干扰的磁共振包络信号,时域数据的虚部SI(k)可通过计算转换为磁共振包络信号中残余噪声。
13.对SR(k)和SI(k)分别进行傅里叶变换,得到频谱FR(ω)和FI(ω),图10所示为时域虚部数据SI(k)的时域图(图10A)和频域图(图10B),频域实部实线曲线为奇对称,频域虚部虚线曲线为偶对称。在FI(ω)频谱中,对ω=2326Hz-2500Hz=-174Hz处的幅度乘因子-1,使频域实部实线曲线转变为偶对称,频域虚部虚线曲线转变为奇对称,频谱FT(ω)如图11B图所示,经傅里叶反变换为时域数据后全部为实数,也就是磁共振包络信号中的残余噪声,其曲线图如图11A所示。从频域减去噪声估计频谱得到转换后的频谱FC(ω)=FR(ω)-FT(ω),以及其傅里叶反变换曲线如图12所示,为磁共振包络信号的频域图(图12A)和时域图(图12B)。
14.对频谱FC(ω)在频域进行调制,将频谱幅度缩放并将频谱移动到以ω=2326Hz为中心处,得到修正后的磁共振信号频谱F(ω),再对F(ω)进行傅里叶反变换,得到消减了残余工频噪声和高斯白噪声后的核磁共振信号,如图13所示为频域图13A和时域图13B。
15.对核磁共振信号数据S(k)中所有噪声成分采用步骤12~14所述的频域对称法,消除残余工频噪声和随机噪声,得到最终的核磁共振信号,其时域图(图14A)和频域图(图14B)如图14所示。
以上所述仅为本发明的较佳实施例而已,并不用以限制本发明,凡在本发明的精神和原则之内所作的任何修改、等同替换和改进等,均应包含在本发明的保护范围之内。