最优传输论文（一）Sliced Wasserstein Discrepancy for Unsupervised Domain Adaptation

提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档

---

前言

本文通过利用特定于任务的决策边界和Wasserstein度量实现领域之间的特征分布对齐。
提出的切片Wasserstein差异(SWD)旨在捕捉特定于任务的分类器的输出之间不相似的自然概念。
我们的方法旨在通过利用Wasserstein度量来最小化在特定任务分类器之间移动边际分布的成本。
本文的几个关键贡献:
(1)通过最优传输理论(即Wasserstein距离)和任务特定决策边界来对齐域之间的特征分布的一种新颖的原则性方法。
(2)利用切片Wasserstein差异(Wasserstein度量的变分公式)实现高效的端到端训练。
(3)以对抗方式优化切片Wasserstein差异，有效地利用底层流形的几何形状。
(4)该方法跨越了多个任务，并且可以很容易地应用于任何领域适应问题，如图像分类、语义分割和目标检测。

深度JDOT方法在JDOT的基础上进一步改进，在深度神经网络层中联合匹配特征和标签空间分布，具有更强的鉴别性特征表示。然而，这些方法在标签空间中显式地强制源样本和目标样本之间的一对一映射，这在很大程度上限制了平衡源目标对不可用时的实际使用。

本文框架：
通过任务特定决策边界和Wasserstein距离进行分布对齐。Wasserstein度量作为任务特定分类器之间的可靠差异度量，它直接度量目标样本与源样本的支持程度，而不是在标签空 间中产生显式的一对一映射。

3.Methods

首先在3.1节介绍无监督域自适应设置。其次，我们在第3.2节简要回顾了最优运输的概念。最后，我们在3.3节详细介绍了如何用切片Wasserstein差异训练所提出的方法。

3.1 Framework Setup

无监督域自适应的目标是建立从标记源集到未标记目标集的知识转移。当两个数据分布Xs和Xt足够接近时，只需将注意力集中在**最小化联合概率分布P(Xs, Ys)**的经验风险上。
根据最大分类器差异(Maximum Classifier difference, MCD)框架，我们训练了一个特征生成器网络G和分类器网络C1和C2，它们接受从G生成的特征响应，并分别生成相应的logits p1(y|x)、p2(y|x)(如图1所示)。
(logits即为全连接层输出)

优化过程包括三个步骤:
(1)在源域{Xs, Ys}上训练生成器G和分类器(C1, C2)对源样本进行正确的分类或回归:

Ls可以是任何损失函数，如交叉熵损失或均方误差损失。

(2)固定生成器G，更新分类器(C1, C2)，使目标集Xt上两个分类器输出的差异最大化，识别出任务特定决策边界支持之外的目标样本：

其中LDIS(Xt)为差异损失。
在此步骤中还加入Ls(Xs, Ys)以保留源域信息。

(3)冻结两个分类器的参数并更新生成器G，使两个分类器在目标集Xt上的输出差异最小化：

这一步使目标域特征簇更接近源域

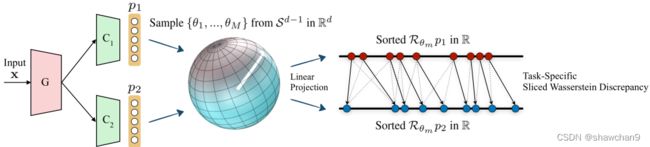
图1:提出的切片Wasserstein差异(SWD)计算的说明。SWD的设计目的是在任务特定分类器C1和C2之间捕获Rd(d维空间)中概率度量p1和p2的不相似性，它们从特征生成器g获取输入。SWD通过在单位球Sd−1上的均匀度量上使用放射投影的Wasserstein度量的变分公式直接实现端到端训练，为检测远离源支持的目标样本提供了具有几何意义的指导。详情请参阅第3.3节。

3.2. Optimal Transport and Wasserstein Distance

在上述MCD框架中，域自适应的有效性完全取决于差异损失的可靠性。没有差异损失的学习，本质上是去掉训练过程中的第2步和第3步，只是在源域上进行监督学习。
设Ω为概率空间，µ，ν为P(Ω)中的两个概率测度，Monge问题寻求代价最小的输运图T: Ω→Ω

其中T# µ= ν表示从µ到ν ∀ Borel子集A⊂Ω的一对一推进， c: Ω × Ω→R+是一个geodesic度量，可以是线性的，也可以是二次的。

Kantorovitch[27]提出了公式4的一个松弛版本，它寻求一个联合概率分布γ∈P(Ω × Ω)的运输方案，使得：

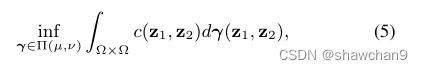
其中Π(µ,ν)={ γ∈P(Ω×Ω) | π1 # γ=µ，π2 # γ=ν}和π1和π2表示Ω×Ω到Ω的两个边缘投影。解 γ* 称为最优传输计划或最优耦合。
当q≥1时，P(Ω)中µ与v之间的q- wasserstein距离定义为

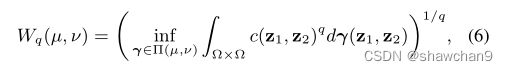
这是由最优运输计划引起的最小成本。在我们的方法中，我们使用1-Wasserstein距离，也称为earth mover距离(EMD)。

3.3. Learning with Sliced Wasserstein Discrepancy

为了充分利用两方面的优势——利用特定任务的决策边界来对齐源和目标的分布，并将Wasserstein差异(它对随机梯度下降训练具有良好的能量景观)纳入我们的框架，我们建议使用切片Wasserstein差异将W1(p1, p2)集成到我们的框架中，分类器输出p1和p2之间沿放射投影的1-Wasserstein距离的一维变分公式。
根据[52]定义的离散度量的切片重心，我们将切片1-Wasserstein差异(SWD)定义为

其中Rθ表示概率测度µ或ν上的一维线性投影运算，θ是Rd中单位球Sd−1上的均匀测度，使得积分Sd−1 dθ = 1。这样，计算切片Wasserstein差异等价于求解几个具有封闭解[52]的一维最优输运问题。
具体而言，设α和β为N个样本的N个一维线性投影排列，使∀0≤i一维Wasserstein距离最小的最佳耦合γ*。对于离散概率度量，我们的SWD可以写成:

M为随机抽样θ， c为二次损失。我们提出的SWD本质上是原始Wasserstein距离的变分版本，但计算成本只有它的一小部分。

总结

本文开发了一种新的无监督域自适应方法，该方法通过测量任务特定分类器之间的切片Wasserstein差异来对齐分布，与Wasserstein度量的联系为更好地以有效的方式利用其有几何意义的嵌入铺平了道路，